鬼の極難マフィン問題 – 2023年東大数学第6問

型からはみ出た部分が特にヤバイ（Gundula VogelによるPixabayからの画像）

2023年3月8日2023年3月15日

　2023年東大数学第6問は図形の問題ですが、このジャンルでは最も難しいものの一つに数えられるでしょう。問題文は以下のとおりです。

　Oを原点とする座標空間において、不等式 $|x| \leqq 1, |y| \leqq 1, |z| \leqq 1$ の表す立方体を考える。その立方体の表面のうち、 $x < 1$ を満たす部分をSとする。
　以下、座標空間内の2点 A,B が一致するとき、線分 AB は点 A を表すものとし、その長さを0と定める。

(1) 座標空間内の点 P が次の条件 (i)、(ii) をともに満たすとき、点 P の動きうる範囲 V の体積を求めよ。
　(i) $\mathrm{OP} \leqq \sqrt3$
　(ii) 線分 OP と S は、共有点を持たないか、点 P のみを共有点に持つ。

(2) 座標空間内の点 N と点 P が次の条件 (iii)、(iv)、(v) をすべて満たすとき、点 P の動きうる範囲 W の体積を求めよ。必要ならば、 $\sin \alpha = \displaystyle\frac 1{ \sqrt{3}}$ を満たす実数 $\alpha \displaystyle\left( 0 < \alpha < \displaystyle\frac{\pi}2 \right )$ を用いてよい。
　(iii) $\mathrm{ON + NP} \leqq \sqrt3$
　(ii) 線分 ON と S は共有点を持たない。
　(ii) 線分 NP と S は、共有点を持たないか、点 P のみを共有点に持つ。

　なぜマフィンなのかは、おいおい明らかになります。

　問題文が少々くどいですが、東大ではよくあることなので、これだけで危険を察知することは難しいでしょう。しかし本問こそが、回答時間を無限に吸い取る恐怖の大王です。

　まんじゅうならぬ「マフィン恐い」な本問。早速見ていきましょう。

小問1の解法

空間図形 V の形状を把握する

　まず、図形 V がどんな形なのかを把握します。

　図形 S というのは、簡単に言うと蓋の空いた立方体です。 V というのは、 S の中央 O に光源を置いたとき、 S に遮られずに O を見通すことが出来、かつ O からの距離が $\sqrt 3$ 以下である点の集合です。

　 O と、 S の各頂点の距離が $\sqrt 3$ なので、S の内部はすべて V に含まれることがわかります。

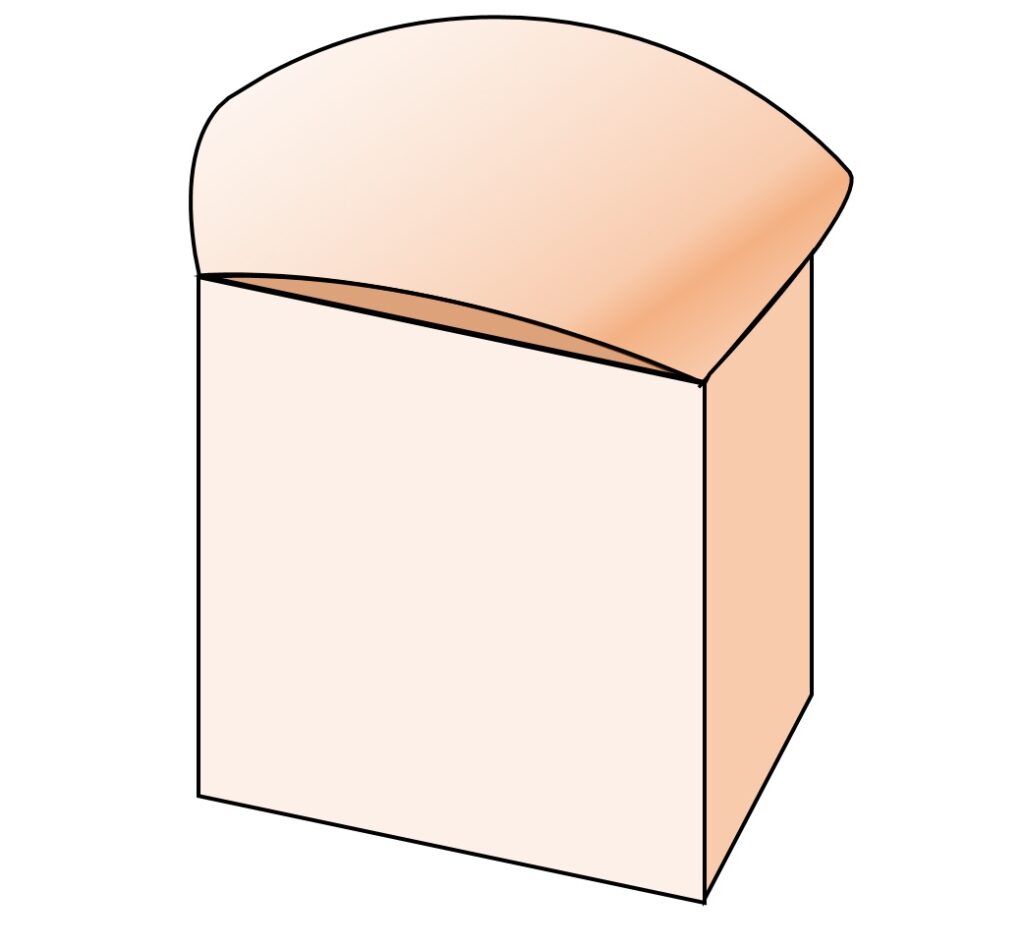
　あとは、 S の蓋の空いた上方に、どれくらい張り出しているかですが、 O からの距離が $\sqrt 3$ 以下という条件があるので、半径 $\sqrt 3$ の球面が乗った形となります。四角い型で作ったマフィンのような形状です(図１)。

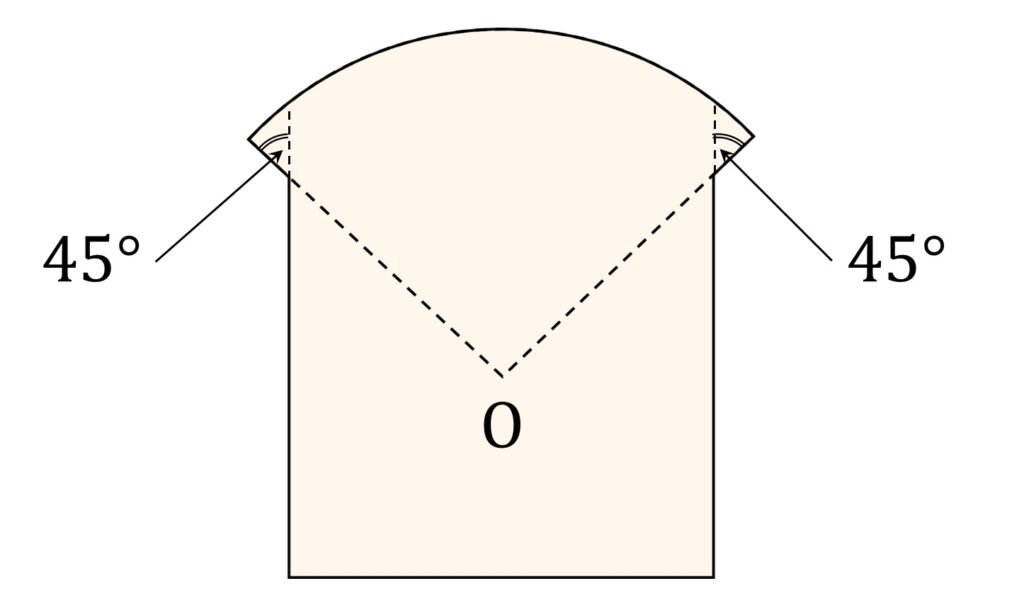
　また、球面は S の側面を超えて外側に張り出しますが、そのオーバーハングは45°となります(図２)。

V をコーン部分と箱部分に分解する

　ここで、 V を球面から O までの四角錐っぽい図形（コーンと名づけます）と、それを取り去った残りの箱部分に分解します(図３)。

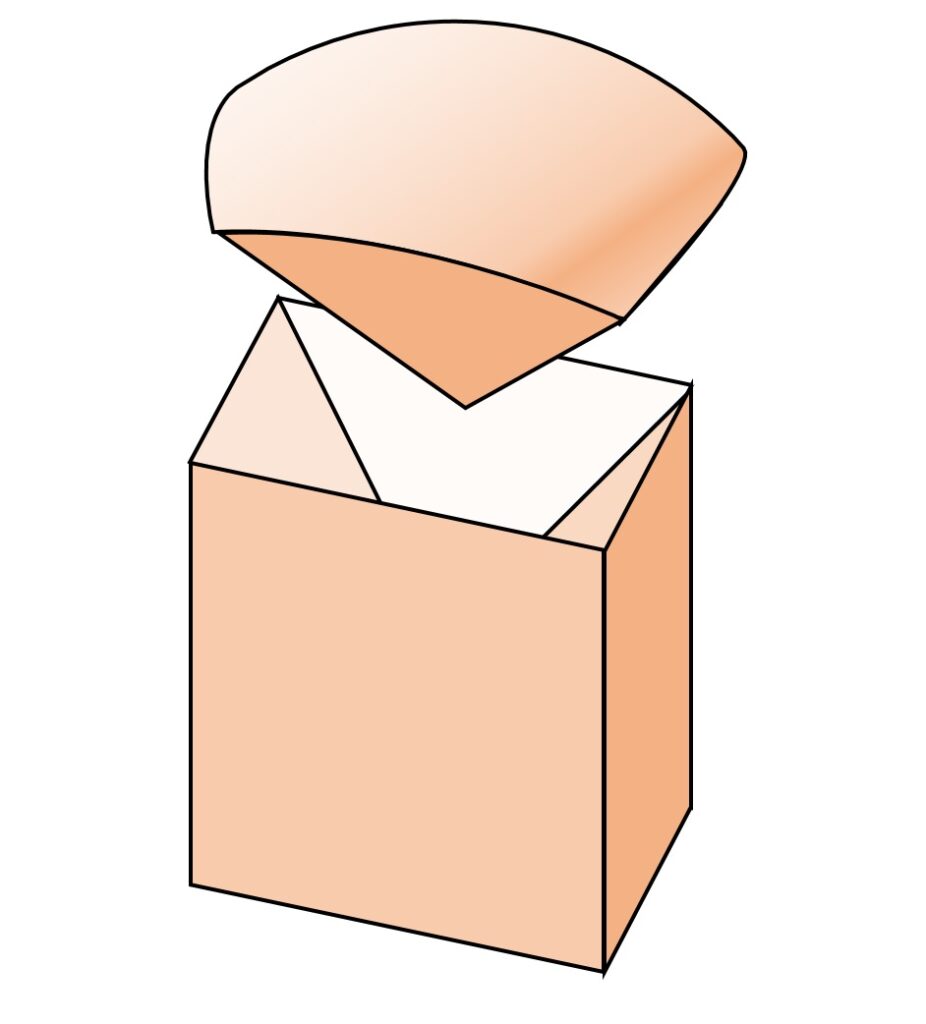
　箱部分の体積は容易に求めることが出来て、

2^3 - 2^2 \times1 \div 3 = \frac {20}3

です。

コーン部分の体積を求める

　残りはコーン部分の体積です。最初は極座標変換で容易に積分できるかと思ったのですが、思ったより難しかったので断念しました。もっと楽な方法を模索します。

　ヒントを探るため、コーンを含む球面全体を上から見たところを、図示してみました（図4）。簡単に計算できそうな気もしますが、やはり思いつきません。そこで、コーン部分の底面である非ユークリッド的正方形の外側に在る、非ユークリッド的三角形を底とするコーンなら計算できるかと考え、どんな形か確認するため、これが正面に来るように球面を回転させます(図４の赤や紫の部分)。

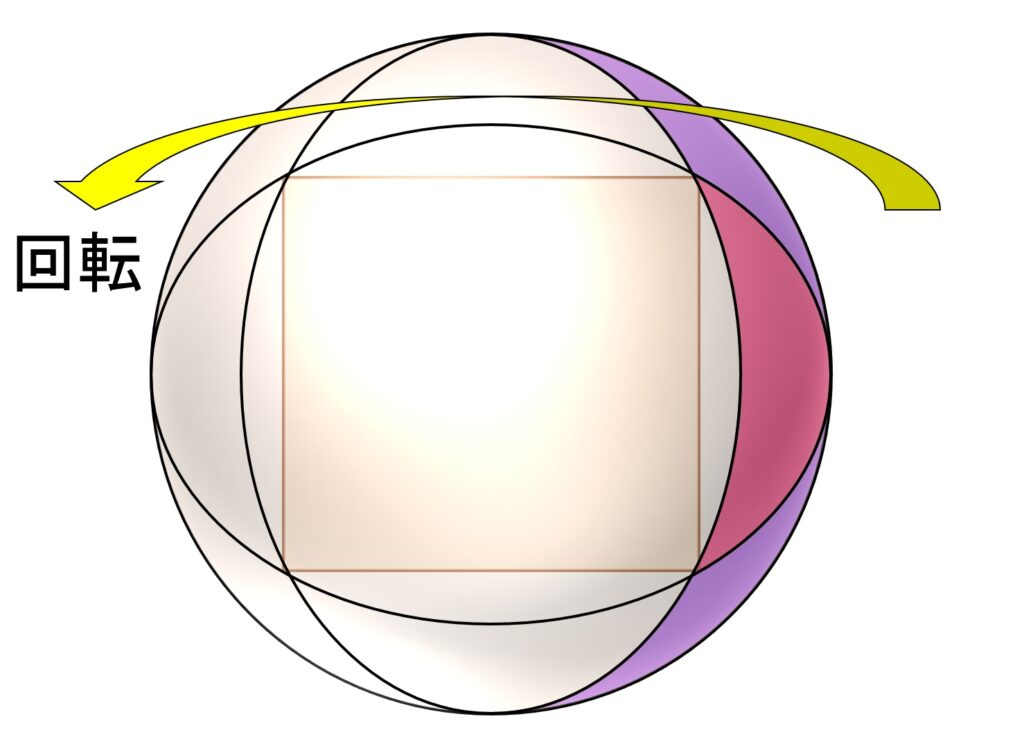
　ここで驚くべきことに、それらの非ユークリッド三角形は、立方体の別の面を開口してできる非ユークリッド正方形の一部であることがわかりました(図５)。

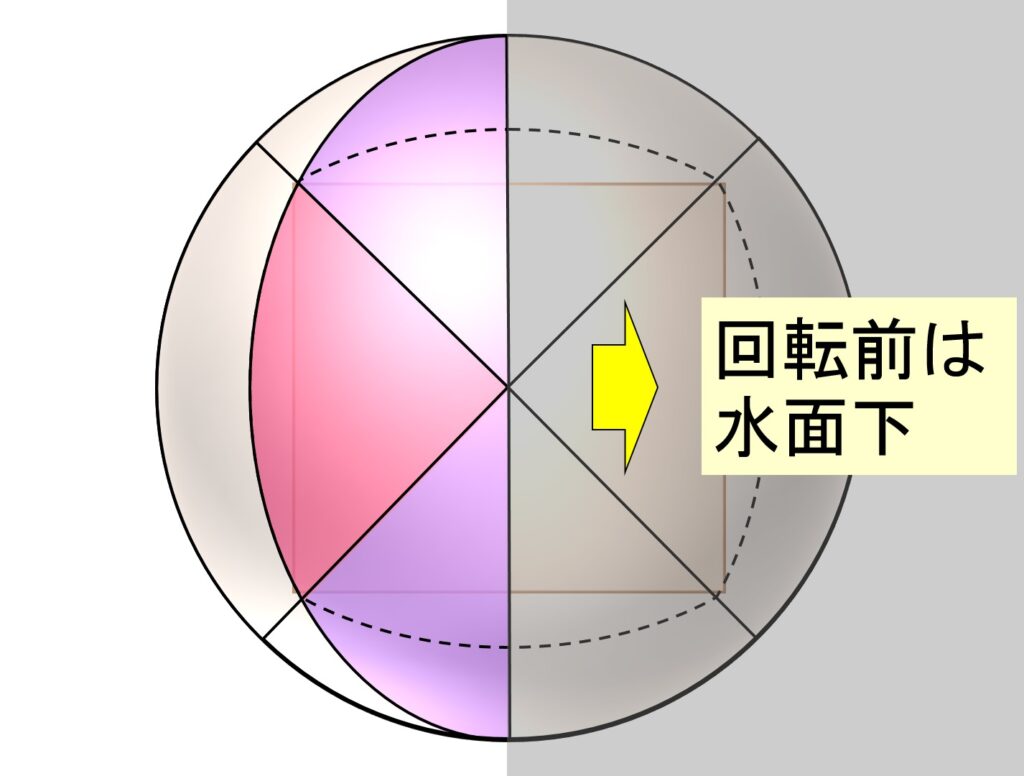
　ここから、球面は6つの非ユークリッド正方形で分割されることがわかります。実際、球面上の任意の点 P と O を結ぶとき、線分 OP は立方体のいすれか一つの面と交点を持つか、辺のいずれかと交点を持つかの、いずれかなので、球面は中心 O を光源として、立方体の各面が球面に投影されてできる6つの非ユークリッド正方形に、重複なく分割されます。