n = 3m +2 ( m は非負整数)の時の証明
残りは、nを3で割った余りが2のとき、どうなるかです。おそらく白オセロ列は出来ないだろうと予測できますが、これの証明が超絶難問です。オセロ列生成の操作が2種類ある上に、それぞれの操作によって増減する白オセロ/黒オセロの数、およびそれらの位置変化が異なるので、例えば白オセロの数を使った数学的帰納法や背理法では、場合分けが複雑になりすぎて、訳が分からなくなります。
証明の方針
あるオセロ列が1個の白オセロから操作1及び操作2を施して生成されたものであるための必要条件を導出し、長さ 3m+2 の白オセロ列がそれを満たさないことを示すことによって、白オセロ列が出来ないことを証明します。
記号の定義
証明に当たって、以下の記号を定義しておきます。
\mathfrak{G} = \{ すべてのオセロ列 \}
G = \{ 1個の白オセロを起点に、操作1および操作2を施して生成されるオセロ列 \}
つまり、 \mathfrak{G} は、特に何も考えずに1列につなげたオセロ列の集合、 G は題意に沿って、1個の白オセロから生成されたオセロ列の集合です。当然、 G \subset \mathfrak{G} が成り立ちます。
拡張オセロ列
オセロ列への操作が2種類あるため、より訳が分からなくなってしまうのですが、仮にオセロ列の「端」がなくなれば、操作1が不要になって、証明が簡素化されることが期待できます。
そこで、初期状態の1個の白オセロの両端に黒オセロをそれぞれ付け加えて、3個状態にし、これに操作2のみを加えてオセロ列を生成します。こうやって生成されたオセロ列を拡張オセロ列と呼び、その集合を EG と定義します。
EG = \{ ●-〇-●から操作2のみを施して生成された拡張オセロ列 \}
EG も G 同様、 \mathfrak{G} の部分集合です。
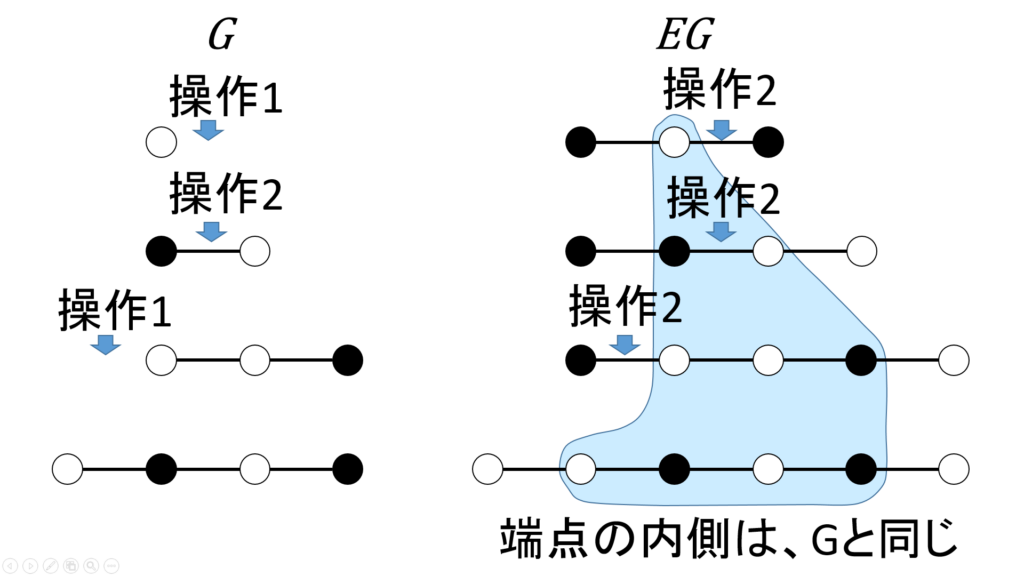
EG の各要素は、両端のオセロを1個ずつ取り去ることによって、元のオセロ列集合 G と、操作も含めて1対1対応します(図5)。
ここで、オセロ列 g \in \mathfrak{G} の左右両端にオセロの石 o_L,o_R \in \{ ○,● } をそれぞれ接続するとき、これを
o_L - g -o_R
と表記することにします。このとき明らかに、以下の命題が成り立ちます。
命題2
\bm{g \in G } ならば、ある \bm{o_L,o_R \in \{ } ○,● } が存在して、 \bm{o_L - g -o_R \in EG } が成り立つ。
命題2の対偶を取ることにより、直ちに次の系を得ます。
系1
\bm{o_L,o_R \in \{ } ○,● } をどのように選んでも \bm{o_L - g -o_R \notin EG } であるとき、 \bm{ g \notin G } である。