キング オブ 難問 – 1998年東大 数学 後期 第3問

2021年5月3日2023年12月11日

不変量

　集合 S の不変量とは、ざっくり言うと、ある存在 s がその集合の要素かどうかを判定できる、定量的な尺度のことです。

　ここで、拡張オセロ列集合 EG の不変量を求めます。 EG では操作1は考えなくてよいので、本稿では以降、操作2によって変わらない量を、不変量と呼ぶことにします。

　以下、オセロ列 g \in \mathfrak{G} に対し、不変量を出力する関数すなわち不変量関数 f(g) を導出します。

　このような関数の存在を仮定するとき、 拡張オセロ列集合 EG は、ただ一つのオセロ列 g_0 = ●－〇－●から操作2のみによって生成された集合なので、任意の g \in EG に対し、 f(g) = f(g_0) が成り立ちます。この f(g_0) が、拡張オセロ列集合 EG の不変量です。

不変量関数 f(g) の導出

白オセロの個数に関する考察

　黒オセロと白オセロの間に操作2を行うと、白オセロの総数は１増え、黒オセロの数は変わりませんが、黒オセロをはさんで隣接する2つの白オセロ群において、一方は数が２増え、もう一方は１減少します。（図6）。

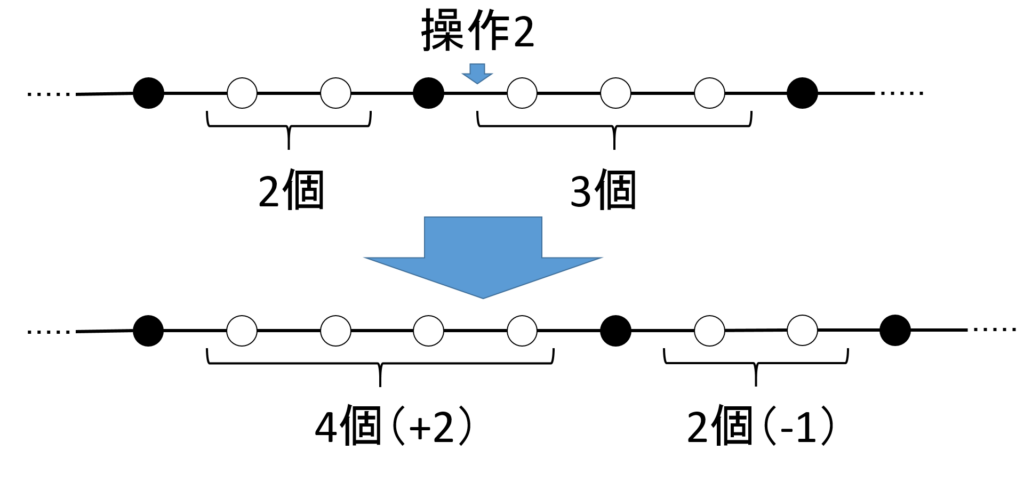
　ここで、隣接する白オセロ群の個数のどちらかの符号を反転させると、オセロ列全体として白オセロが３増えるか、または３減少することになります。すなわち、 \mod 3 で変更がないということです。

　操作2によって変化しない量を考えるには、示唆的な内容ですが、隣り合う白オセロ群個数の一方だけを常に符号反転する、というところから、常に変化が無いようにするには奇数番だけ負にすれば良いんじゃね、と思いつければ、勝ちです。

オセロ列の構造定義

　上記の気づきをヒントに、オセロ列 g \in \mathfrak{G} の構造を、図7のように定義します。

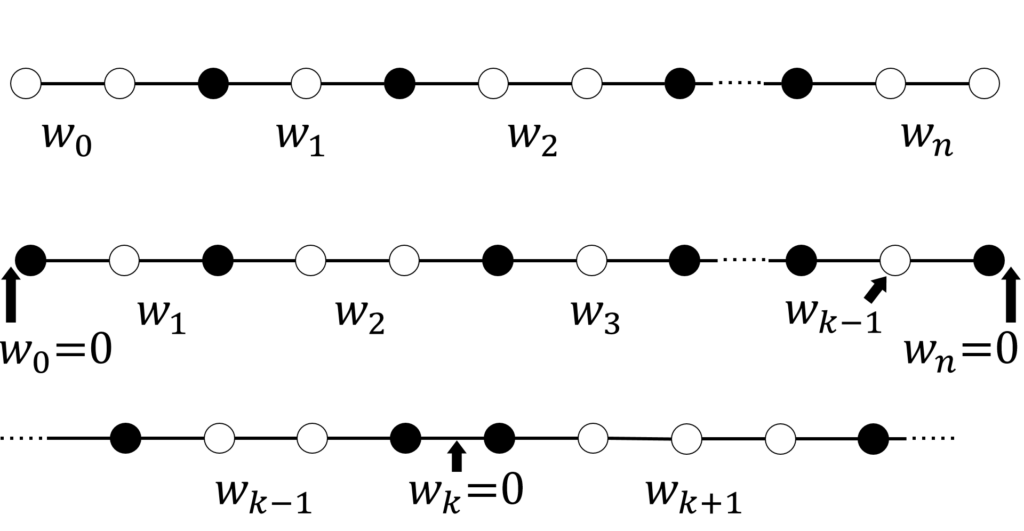
　両端が白オセロであるオセロ列 g において、連続する白オセロを1つの群とし、その個数を左から順に w_k (k=0,1, \cdots ,n) と定義します。(図7上）。

　 g の左端が黒オセロの時は一番左に個数0の白オセロ群が存在していると解釈し、 w_0=0 とします。同様に g の右端が黒オセロの時は、一番右に個数0の白オセロ群があると解釈し、 w_n=0 とします(図7中）。

黒オセロが連続しているときの考え方

　黒オセロは連続していても群にはまとめません。黒オセロと黒オセロの間に個数0の白オセロ群が存在していると解釈し、 w_k=0 とします(図7下）。

　白オセロと黒オセロで群の考え方を変えるのは不自然ですが、実はこうすることによって、〇－〇または●－●の間に操作2を施した場合に、各 w_k の偶奇は変わらなくなります（順番 k が2つ増えるか、2つ減るか、変化しないかのいずれか)。

　この性質は極めて重要です。これがあるため、操作2のたびに w_k の正負を入れ替えるなどと言うことを、する必要がありません。

　図7の定義で、すべての g \in \mathfrak{G} が記述できます。

f(g) の定義

　ここで表記法の定義です。整数 n に対し

n \mod 3

を、 n を3で割った余りとします。

　このとき、オセロ列 g の関数 f: \mathfrak{G} \rightarrow \{ 0,1,2\} を、以下のように定義します。

  f(g) =\sum_{k \text{が偶数} } w_k - \sum_{k \text{が奇数} } w_k    \mod  3 

　すると f(g) は、奇数番の白オセロ数を負にしたおかげで黒オセロと白オセロの間に操作2を施した時に値は変化しませんが、実は〇－〇または●－●の間に操作2を施した場合も、値は変わりません。

　すなわち、すべてのオセロ列 g に対し

f( \text{操作2} (g)) = f(g)

が成り立つので、 f(g) は不変量関数となります。

EG の不変量を求める

　 EG の初期要素 g_0 = ●－〇－●は、 w_0 =0, w_1=1, w_2=0 です。したがって

\begin{aligned}
& w_0-w_1+w_2  \\
&= 0-1+0 \equiv 2 \mod 3
\end{aligned}

であり、

f(g_0 ) = 2

です。以上の考察より、以下の命題が成り立ちます。

命題3

　すべての g \in EG に対し、 f(g)=2 が成り立つ。

　すなわち、 EG の不変量は2です。

　命題3の対偶を取ることで、以下の系を得ます。

系2

f(g) \ne 2 であるオセロ列 g は、 EG の要素でない