今回取り上げる 2008年東大 数学 第3問 は、正八面体の問題です。
以前の記事で、正八面体を扱った問題を紹介しました(1990年前期 第3問)。その年に生まれた人が受験期を迎えた正にその年、あの正八面体の脅威が、再び人類(の中の東大受験者)を襲う!!
というわけで今回の問題、前回と比べて訳分からん度が、大幅UPしています。問題文は以下の通りです。
- 正八面体のひとつの面を下にして水平な台の上に置く。この八面体を真上から見た図(平面図)を描け。
- 正八面体のたがいに平行な2つの面をとり、それぞれの面の重心を G_1 、 G_2 とする。 G_1 、 G_2 を通る直線を軸としてこの八面体を1回転させてできる立体の体積を求めよ。ただし八面体は内部も含むものとし、各辺の長さは1とする。
小問1の解法
正八面体の一つの面を下にして置け、などと言われても、全然イメージできません。そこで、正八面体を2つの四角錘に切断し、その1つを、三角の面を下にして地面に置いてみます。イメージとしては、ピラミッドを横にごろんと転がした感じです(図1)。
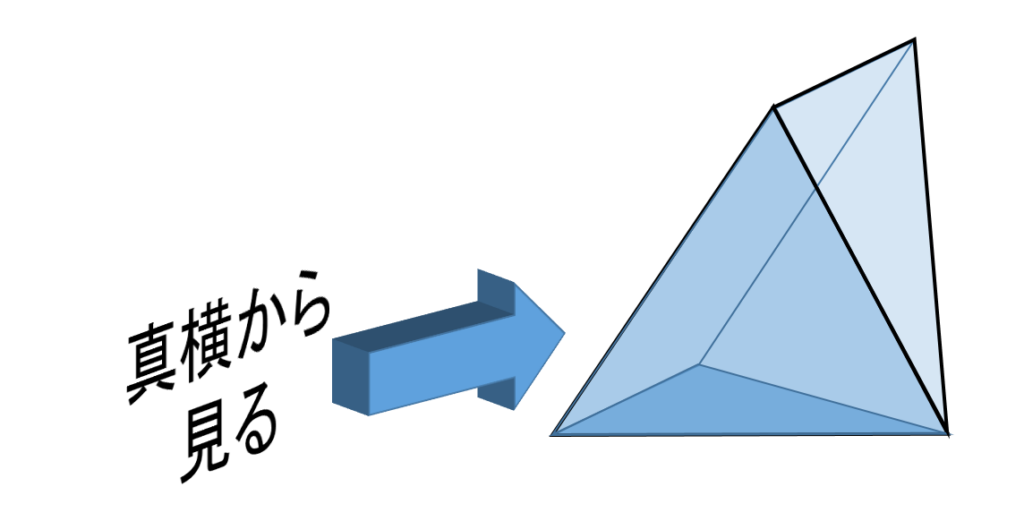
この図形を真横から見て、ピラミッドの底面だった正方形の天辺がどの位置に来るか、確認します(図2)。以降、正八面体の一辺の長さが1であるとして、各図の長さを計算してあります。
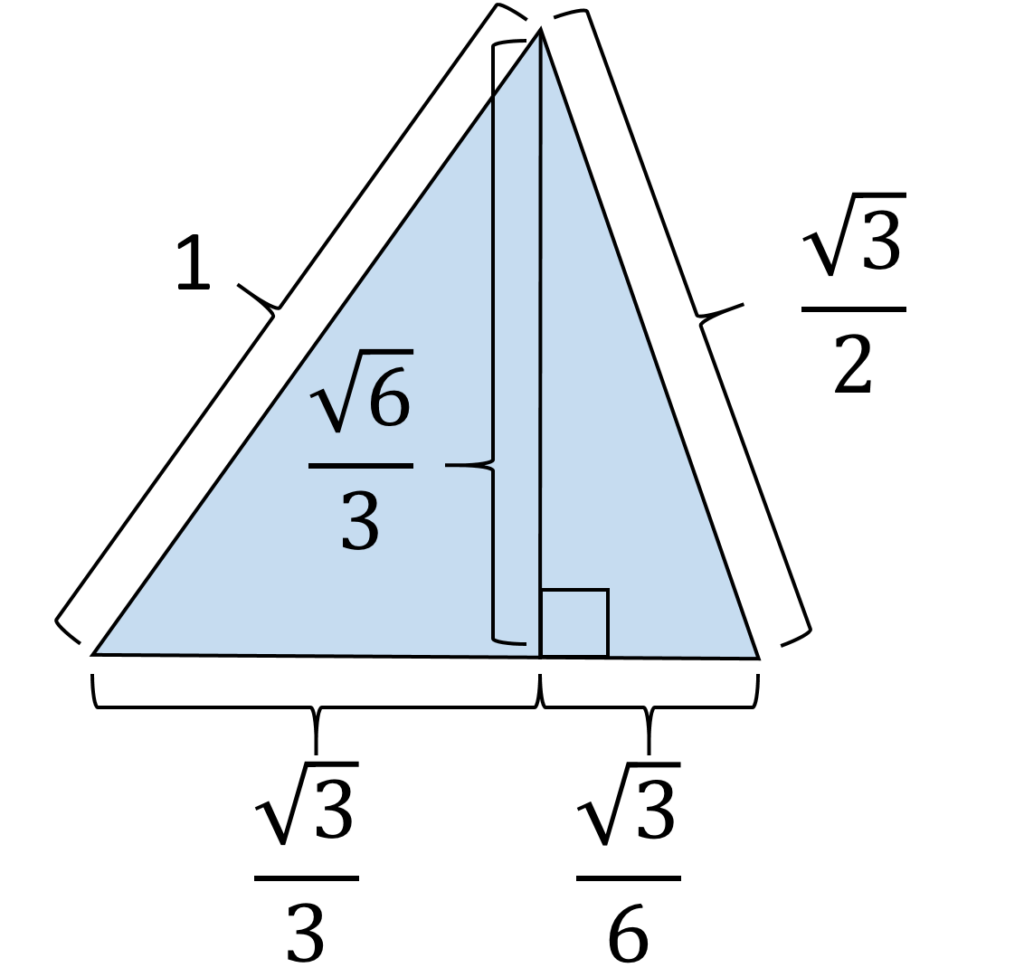
図2の通り、天辺は、現状の底面である正三角形の高さを2:1に内分する位置を通ります。
この情報をもとに、今度は図1を真上から描きます(図3)。
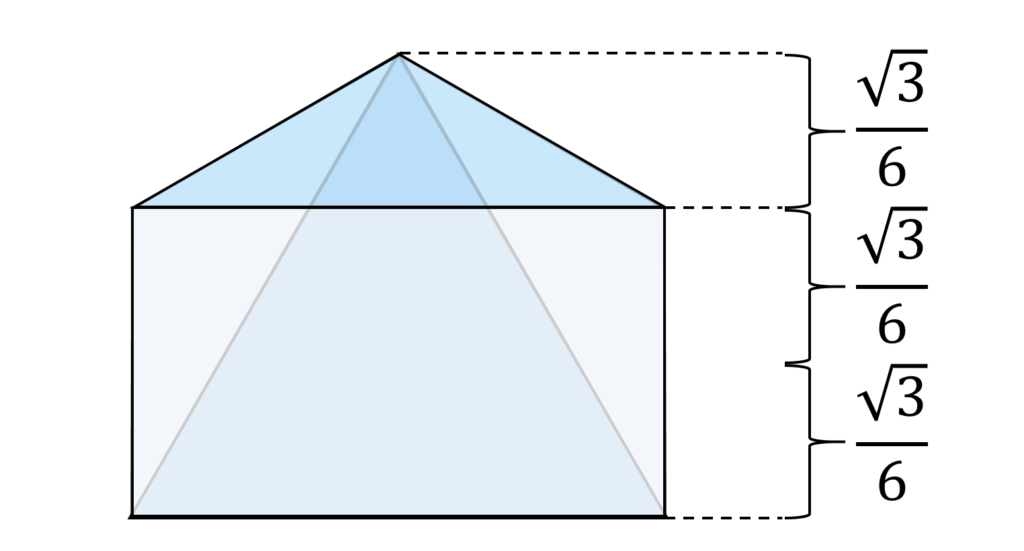
ピラミッドの底面だった正方形が、上から見ると長方形に見えることに注意すれば、この図は容易に描けると思います。
この図を上下ひっくり返して、「裏返し」て、ピラミッド底面が一致するように置けば、求める「上から見た正八面体」の出来上がりです(図4)。
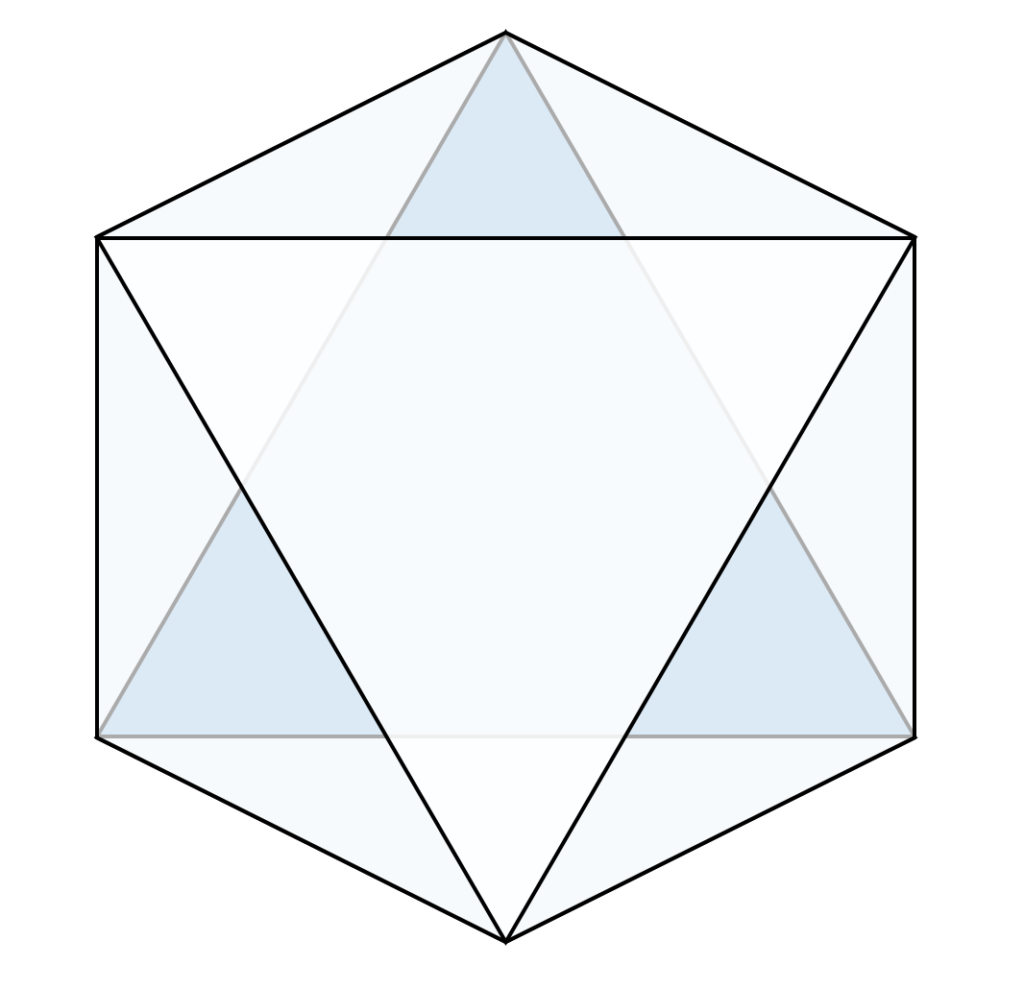
意外なことに、上から見ると正6角形になっていました。これはまったく予想外です。
小問2の解法
まず、底面の重心 G_1 と上面の重心 G_2 が、上から見てどこにあるかを確認します。図3から明らかなとおり、上から見ると G_1 と G_2 は重なって見えます。
つまり、線分 G_1G_2 は底面と垂直です。これは朗報です。斜め方向に回転体の体積など求めさせられた日には、脳みそオーバーヒートで昏倒してしまいます。
線分 G_1G_2 を軸とした回転体の体積を得るには、軸の各点ごとに正八面体表面との距離を求める必要があります。
これを知るには、軸と垂直な面、すなわち底面と平行な面で正八面体を切断したときの断面がどんな形か、知ることが早道です。
ここで、1990年前期第3問にチャレンジした人ならおなじみのあの図形が、再臨します(図5)。
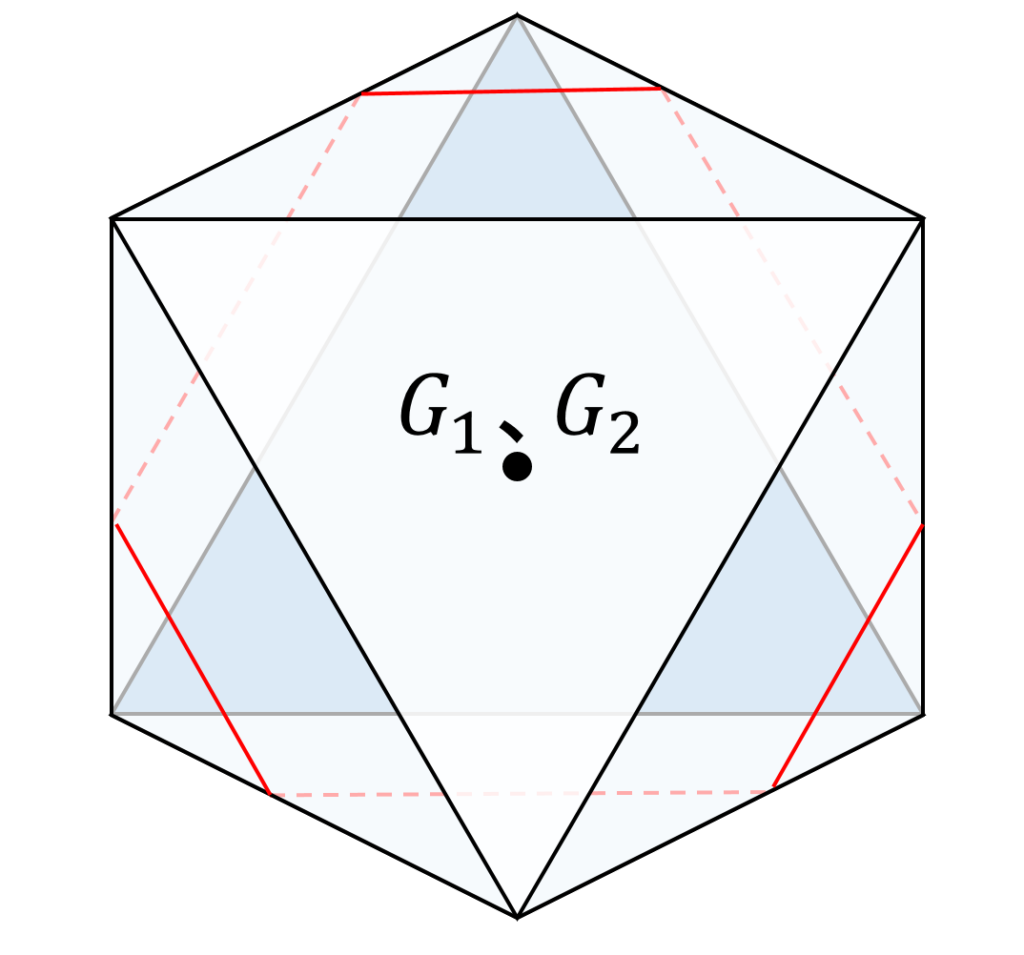
過去のその問題を押さえていた人なら、してやったりとほくそ笑んだことでしょうが、大抵の人は自分の生まれた年の過去問にまで遡ってチェックはしていないでしょう。でも今回は、図4があるので大丈夫です。
切断面は、正八面体の側面の6つの正三角形を、各三角形の底辺と平行に切断します(図6)。これを念頭に置けば、図5は容易に描けると思います。
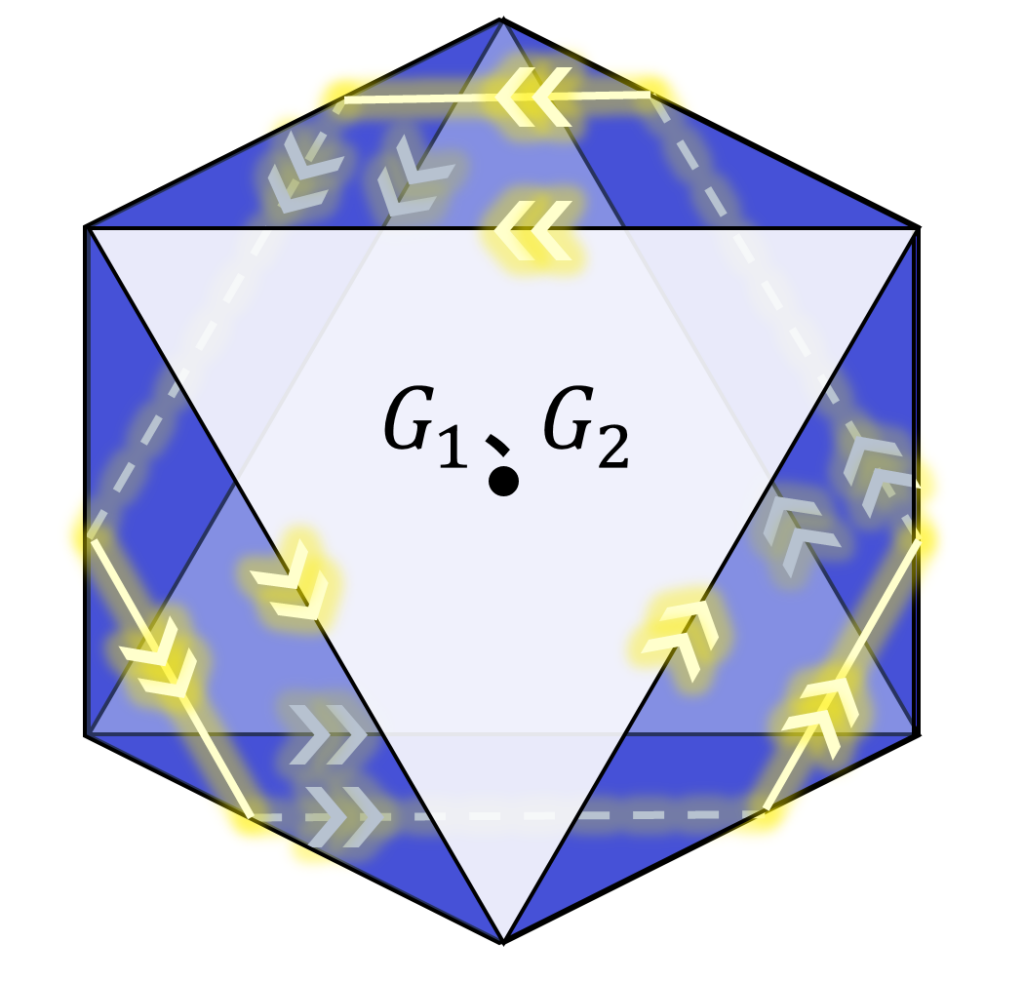
次に、切断面図形の縁と軸との距離の最大値を求めます。切断面図形の「切り欠き」の長さを a \text{ } ( 0 \leqq a \leqq 1 ) と置く時、距離の最大値は、簡単な計算から
\sqrt{ \frac{a^2 - a + 1}{3}}と求められます(図7参照)。
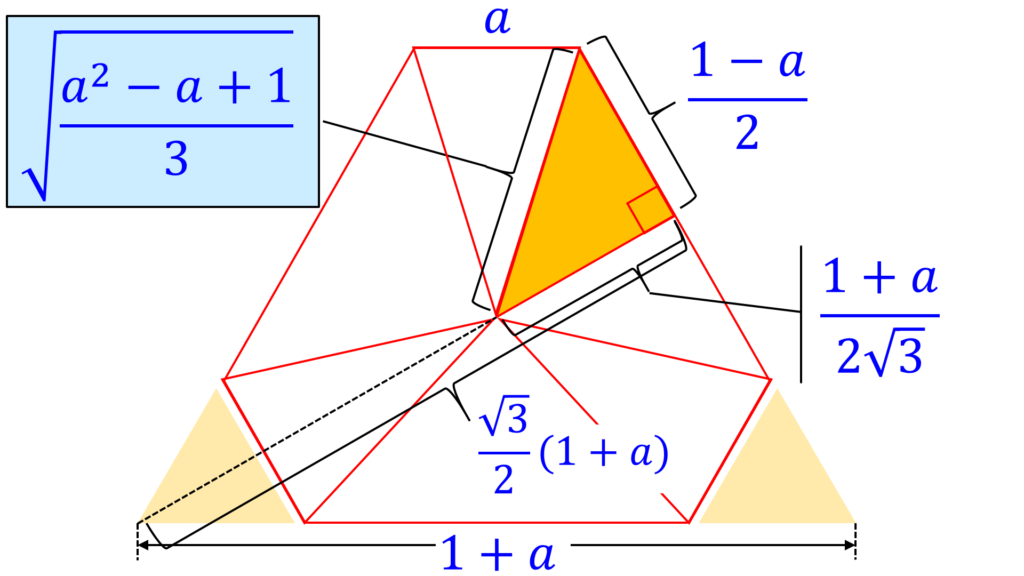
底面からの距離が x のときの、切断面図形の切り欠き a の長さは、 a = \frac{3} {\sqrt{6} }x です。また、図2から明らかなように、 0 \leqq x \leqq \frac{\sqrt{6} } {3} です。これらより、求める体積は
\begin{aligned}
& \pi \int_{0}^{ \frac{ \sqrt{6} }{3} } \frac{a^2-a+1}{3} dx \\
\\
& = \pi \int_{0}^{ 1 } \frac{a^2-a+1}{3} \cdot ( \frac{ \sqrt{6} } {3} ) da \\
\\
& = \frac{5 \sqrt{6} }{54} \pi
\end{aligned}となります。
まとめ
本問は、小問1の図4を書けるかどうかが、すべてです。これが出来れば、小問2で正八面体の断面を求めるのは、割と容易だと思います。
正八面体を1つの面から見たらあんな形になっていることをあらかじめ知っていれば、本問は楽勝ですが、そうでない場合はやはり、小問1の解法で示したように、正八面体を四角錘に分解して、各方向から透視図を描いてみるのが、わかりやすいと思います。