2019年東大 数学 第3問 は、八面体に関する問題です。前回の出題から11年、何度も姿を現すその様は、ティアマト彗星のようです(遭遇周期は必ずしも一定ではありませんが)。
問題文は以下の通りです。
座標空間内に5点 \mathrm A(2,0,0) 、 \mathrm B(0,2,0) 、 \mathrm C(-2,0,0) 、 \mathrm D(0,-2,0) 、 \mathrm E(0,0,-2) を考える。線分 \mathrm {AB} の中点 \mathrm M と線分 \mathrm {AD} の中点 \mathrm N を通り、直線 \mathrm {AE} に平行な平面を \alpha とする。さらに、 p は 2 < p < 4 をみたす実数とし、点 \mathrm P (p,0,2) を考える。
(1) 八面体 \mathrm {PABCDE} の平面 y = 0 による切り口および、平面 \alpha の平面 y = 0 による切り口を同一平面上に図示せよ。
(2) 八面体 \mathrm {PABCDE} の平面 \alpha による切り口が八角形となる p の範囲を求めよ。
(3) 実数 p が(2) で定まる範囲にあるとする。八面体 \mathrm {PABCDE} の平面 \alpha による切り口のうち y \geqq 0 、 z \geqq 0 の部分を点 (x,y,z) が動くとき、座標平面上で点 (y,z) が動く範囲の面積を求めよ。
問題文を一読しただけでは、何のことかわかりません。まず図を描いてみます。以下の通りです(図1)。
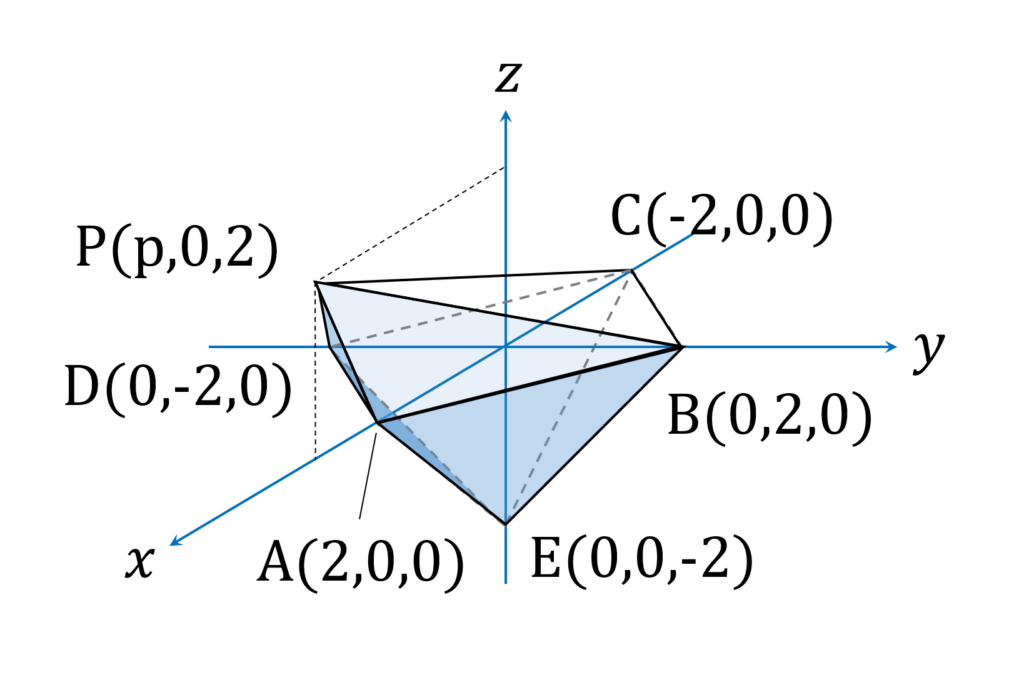
図形の下半分は、上下さかさまのピラミッドです。上半分が曲者で、天頂点が +x 方向にずれています。本当にこれでよいのかと、不安を抱かせる妙な形です。眉間の先が刀状に出っ張った、包丁怪獣ギロンを連想させます。
小問1の解法
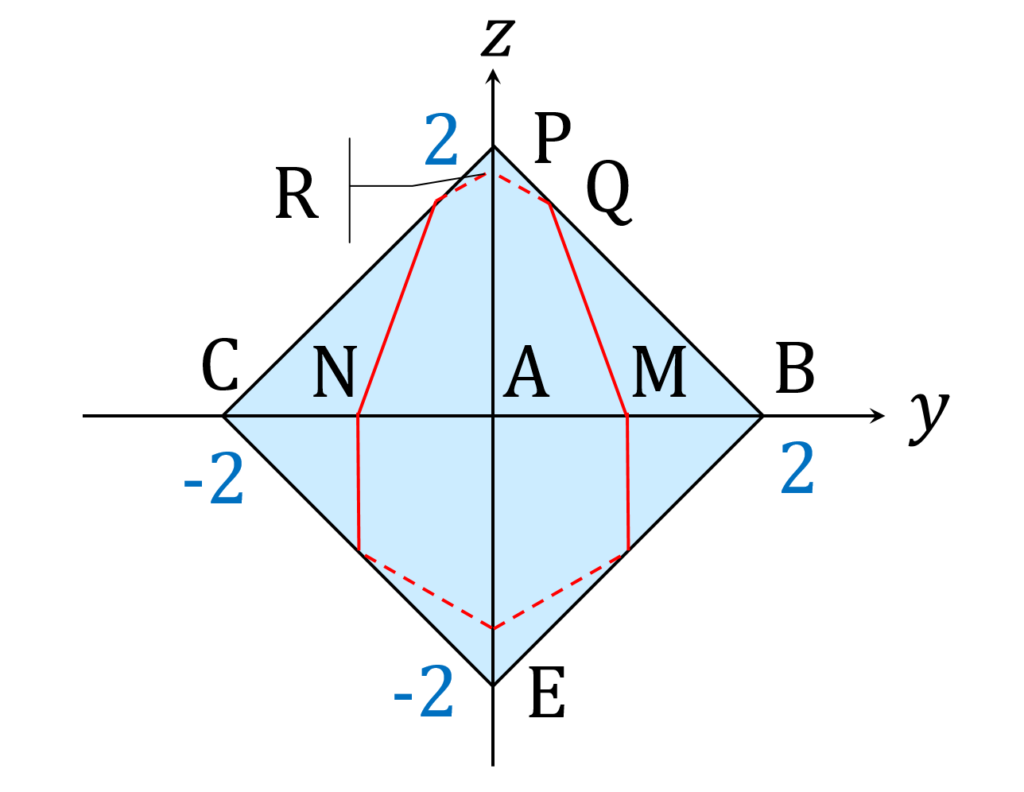
図1を xz 平面で切断した図を描け、というのが小問(1)です。要は、兜割りにしたギロンの断面を描け、ということです。 xz 平面上に存在する \mathrm P 、 \mathrm A 、 \mathrm C 、 \mathrm E の各点をそのままプロットすれば出来上がります。以下のような感じです(図2)。
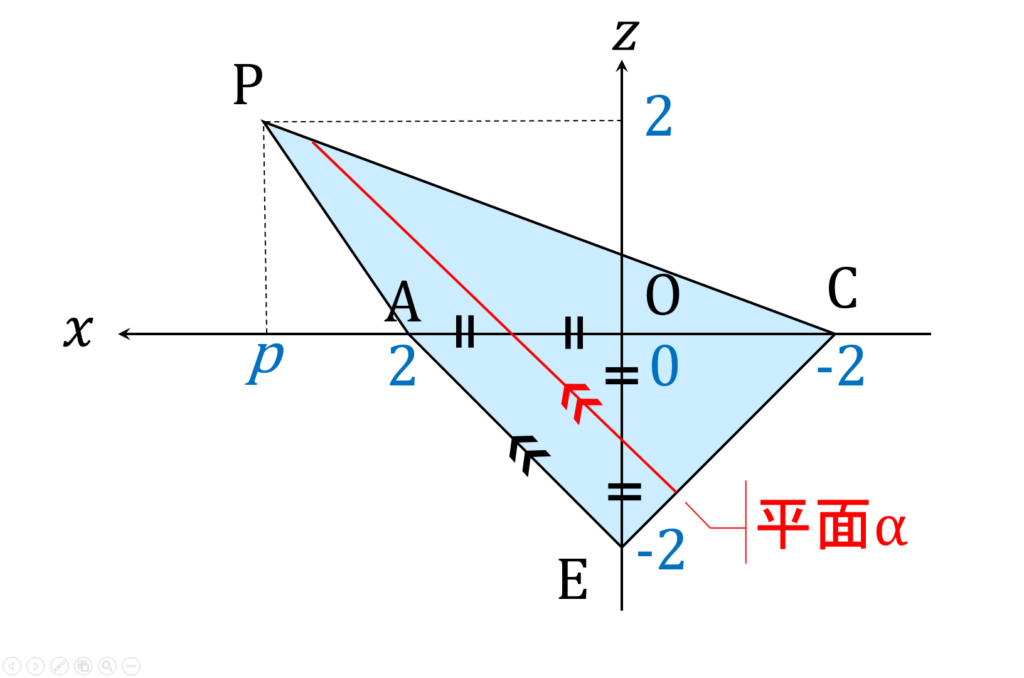
平面 \alpha は辺 \mathrm {AB} および辺 \mathrm {AD} を2等分するので、座標系の原点を \mathrm O とするとき、線分 \mathrm {AO} も2等分します。これと、辺 \mathrm {AE} と平行であるという条件から、平面 \alpha の xz 平面による切り口(直線になります)は、容易に描けると思います。
小問2の解法
平面 \alpha による断面の形を問われています。どんな形なのか、図を描いて把握します。
例によって、上下半分ずつに分けて考えます。まず下半分です。以下の図3のようになります。
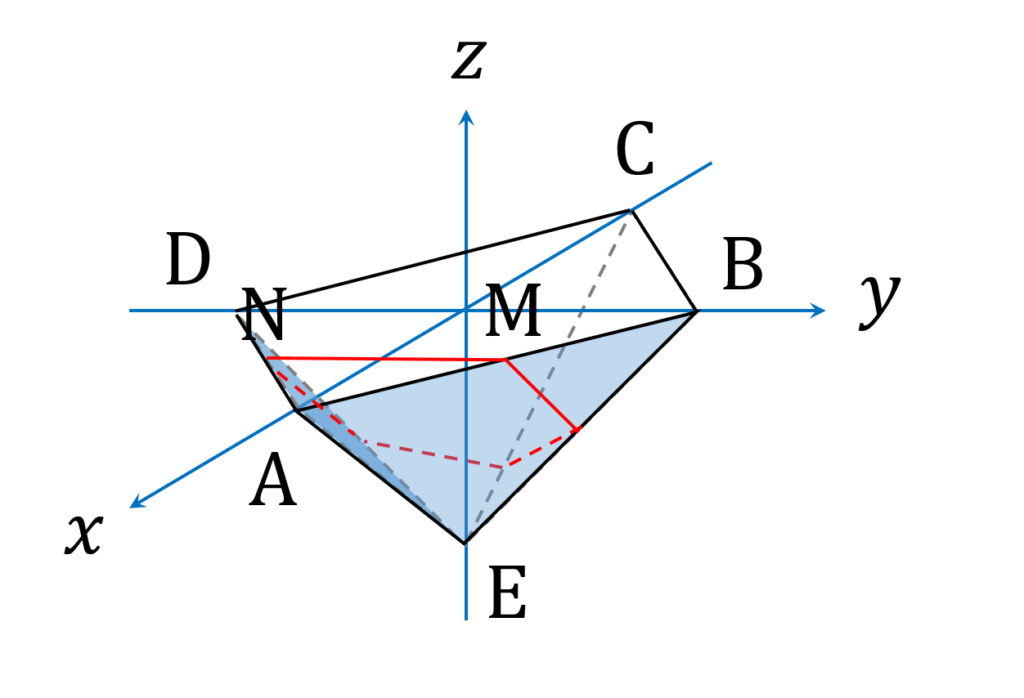
切断面の図形の頂点は、平面 \alpha と各辺の交点になります。平面 \alpha と交わる辺は、 \mathrm {AB} 、 \mathrm {AD} 、 \mathrm {BE} 、 \mathrm {DE} 、 \mathrm {CE} の5本あります。したがって、切断面の図形は5角形です。
次に、問題の上半分です。図を描くと、以下の図4のようになります。
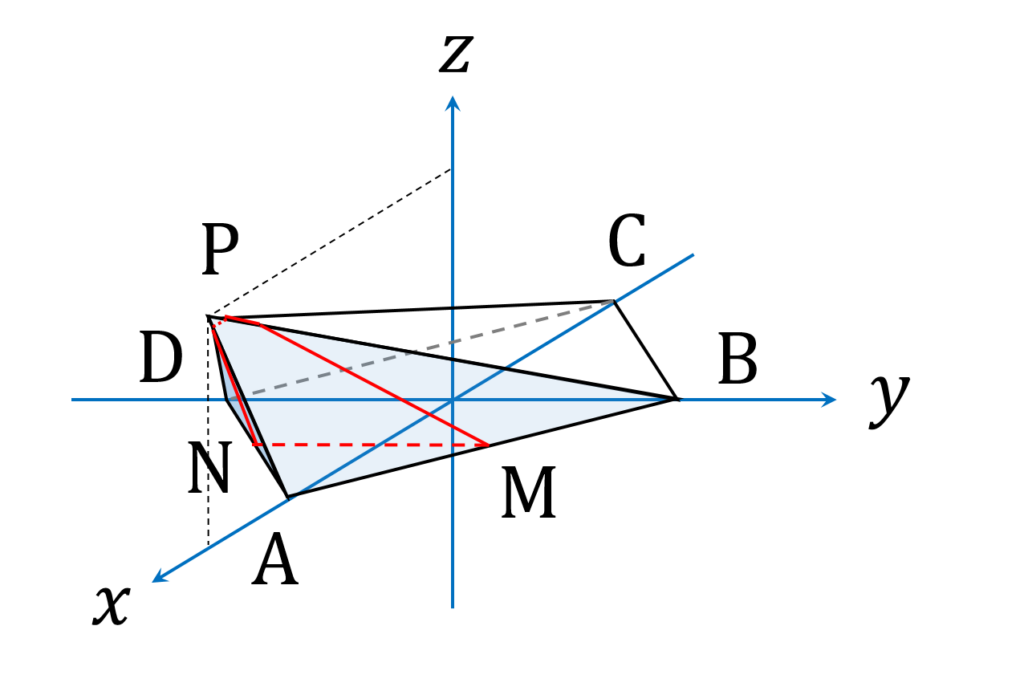
ちょっとわかりにくいですが、こちらの図形でも、平面 \alpha と交わる辺は、 \mathrm {AB} 、 \mathrm {AD} 、 \mathrm {PB} 、 \mathrm {PC} 、 \mathrm {PD} の5本あります。したがって、切断面の図形は5角形です。
先の図形と合わせると、頂点の数は10、そのうち \mathrm M と \mathrm N は共通なので、重複を差し引くと頂点数は8。すなわち、断面の形は確かに八角形です(図5)。
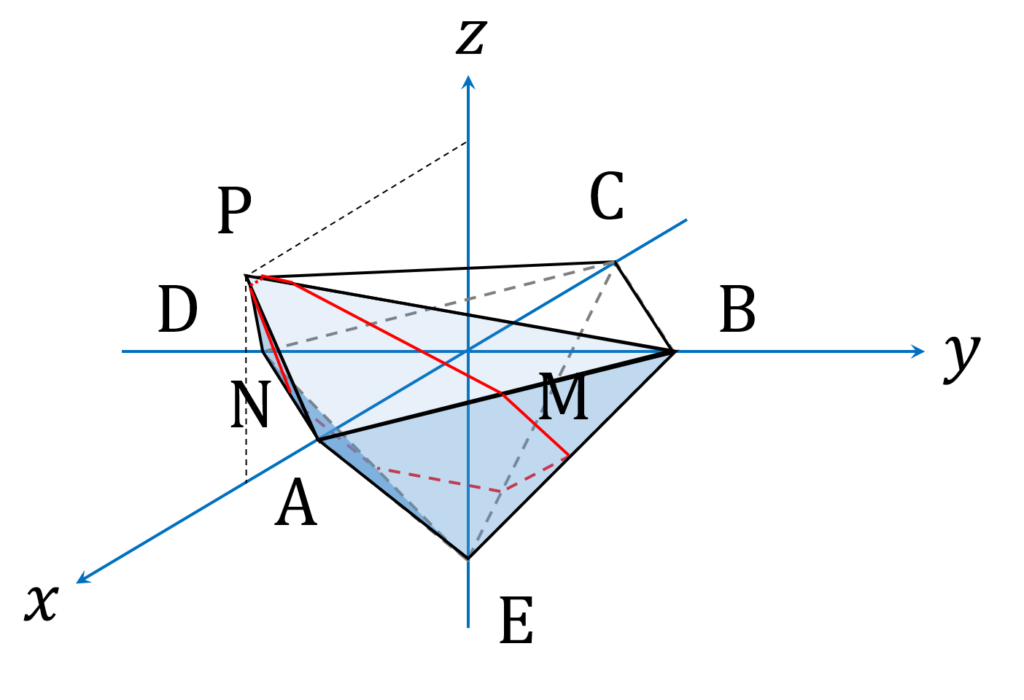
ところで、小問2で求められているのは「断面図が八角形になる p の範囲」です。つまり、 p の値によっては、八角形にならなくなるということです。それはどういう状況でしょうか。
図5のように、ギロンの「鼻先」が前方( +x 方向)に十分長ければ、断面は八角形になりますが、鼻先が短くて平面 \alpha に届かないようだと、辺 \mathrm {PB} 、 \mathrm {PD} が平面 \alpha と交点を持たなくなります。このとき、断面は六角形になります(図6)。
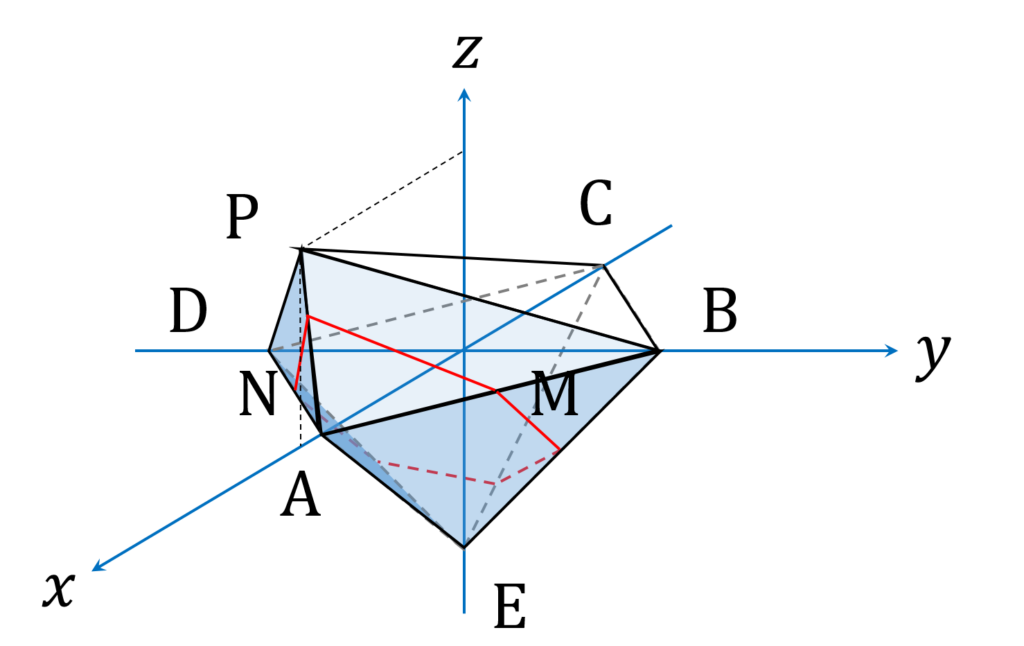
p の具体的な範囲を決めるため、 +y 方向から見た平面図を作成します。平面 \alpha は xz 平面と直交する線分 \mathrm {MN} を含むため、同様に直交します。したがって、 +y 方向から見た平面図上で平面 \alpha は、直線として表現されます。
このことに注意して平面図を作成すると、、 \mathrm {PB} および \mathrm {PD} が平面 \alpha と交点を持つのは 4 > p > 3 の時であることがわかります(図7)。このとき、断面は八角形になります。
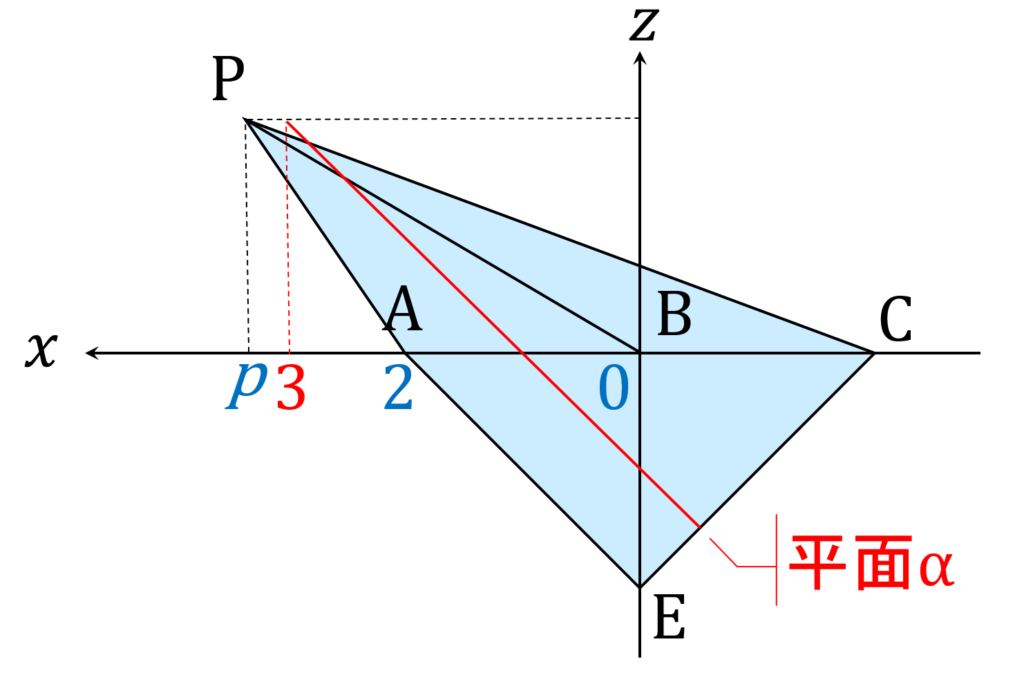
一方、 3 > p > 2 の時は、 \mathrm {PB} および \mathrm {PD} は平面 \alpha と交点を持たないことがわかります(図8)。したがって、 p がこの範囲の時、断面の形は六角形となります。
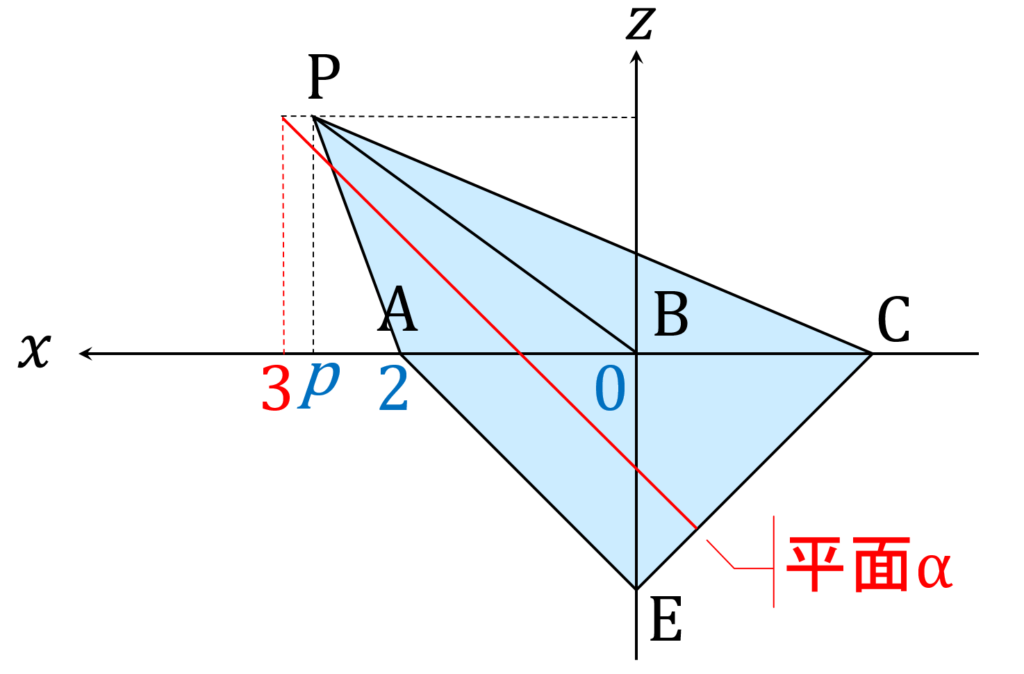
また、 p =3 のときは各線分は一点 p でのみ平面 \alpha と交点を持つので、断面の形はやはり六角形となります。
小問3の解法
3 < p < 4 のとき、断面を xy 平面および xz 平面で切り取った図形を yz 平面に射影します。その面積を求める、というのが小問3のお題です。
yz 平面への射影と言うことは、各点および図形の3次元座標 (x,y,z) から単に (y,z) 座標のみを取り出して、2次元オブジェクトとして考える、ということです。
面積を求める関係上、線分 \mathrm {PB} および線分 \mathrm {PC} と平面 \alpha の交点(それぞれ \mathrm Q 、 \mathrm R とします)の座標を、正確に求める必要があります。
各直線および平面の方程式を求め、そこから交点の座標を求めてもよいのですが、もう少し楽に計算したいので、まずは xz 平面で考えます。
図7から直ちにわかるように、 xz 平面上で線分 \mathrm {PB} の方程式は
z = \frac{2}{p} x線分 \mathrm {PC} の方程式は
z= \frac{2}{p+2}x+ \frac{4}{p+2}平面 \alpha の方程式は
z=x-1
です。これらから Q 、 R の (x,z) 座標を求めると
\begin{aligned}
& \mathrm Q = ( \frac{p}{p-2}, \frac{2} {p-2}) \\ & \mathrm R = (1+ \frac{6}{p},\frac{6}{p})
\end{aligned}次に、各点の y 座標を求めます。 \mathrm R は常に xz 平面上にあるので、 y = 0 です。
図形を +x 方向、つまりギロンの正面から見ると、線分 \mathrm {PB} の方程式は
z = 2 -y
であることがわかります(図9参照)。
これに z = \frac{2}{p-2} を代入することで、 Q の y 座標が求められます。その値は、 y = 2 - \frac{2}{p-2} = \frac{2p-6}{p-2} です。
したがって、各点の座標は
\begin{aligned}
& \mathrm Q = ( \frac{p}{p-2}, \frac{2p-6}{p-2}, \frac{2} {p-2}) \\ & \mathrm R = (1+ \frac{6}{p}, 0,\frac{6}{p})
\end{aligned}となります。面積を求めたい図形の形と各頂点の (y,z) 座標は、以下の図10の通りです。
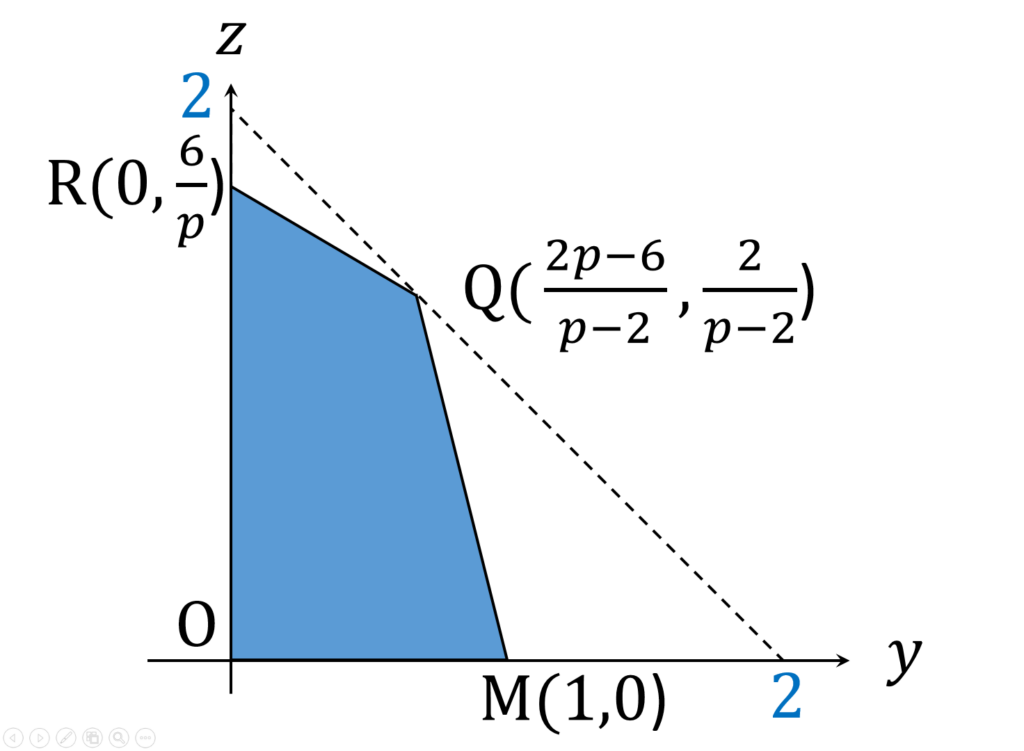
あとは台形や三角形の面積の公式を使って、計算するだけです。直ちに以下の結果を得ます。
\frac{7p-18}{p(p-2)}発展
p=4 のとき、 \triangle \mathrm {ABE} と \triangle \mathrm {PAB} は同一平面になります。
\triangle \mathrm {ABE} の法線ベクトルは明らかに、 (1,1,-1) ですが、 p=4 のとき、 \triangle \mathrm {PAB} の平面方程式は
x+y-z-2=0
となり、その法線ベクトルは \triangle \mathrm {ABE} の法線ベクトルと平行です。
\triangle \mathrm {ABE} と \triangle \mathrm {PAB} は辺 \mathrm{AB} を共有するので、同一平面であるであることがわかりました。
同様に、 \triangle \mathrm {ADE} と \triangle \mathrm {PAD} も同一平面になります。
このとき、断面の形状は六角形になります。もし p の範囲が、 2 < p < 5 とかだったら、 p=4 を除外する必要が出てきたはずです。
このように、面、辺、頂点の数だけで図形の種類を当てようとすると、足元をすくわれることがあります。入試でそこまで意地悪な出題は無いと思いますが、一応念頭に置いておきましょう。
まとめ
本問のような図形の問題は、図を描いてイメージをつかむことが、非常に重要です。特に複雑な形状のものは3面図を描いて、短い時間で形状を把握するよう、心がけてください。
