死角なき難問 – 1996年東大 数学 第3問

2021年7月8日2024年12月9日

l ≧ 2r の場合

　立方体の1辺の長さが l のとき、球の中心を原点とする立体座標系を導入して \mathrm{A_1} (\displaystyle\frac{l}{2},\displaystyle\frac{l}{2},\displaystyle\frac{l}{2}) とおくと、頂点 A₁ から球面の第1象限がすべて監視（と攻撃）できるならば、他の頂点も同様に眼下の象限をすべて監視できるので、監視範囲が全球面を包含します。すなわち S 上のすべての点から A₁,A₂, … ,A₈ のうち少なくとも1点が見えます(図2)。

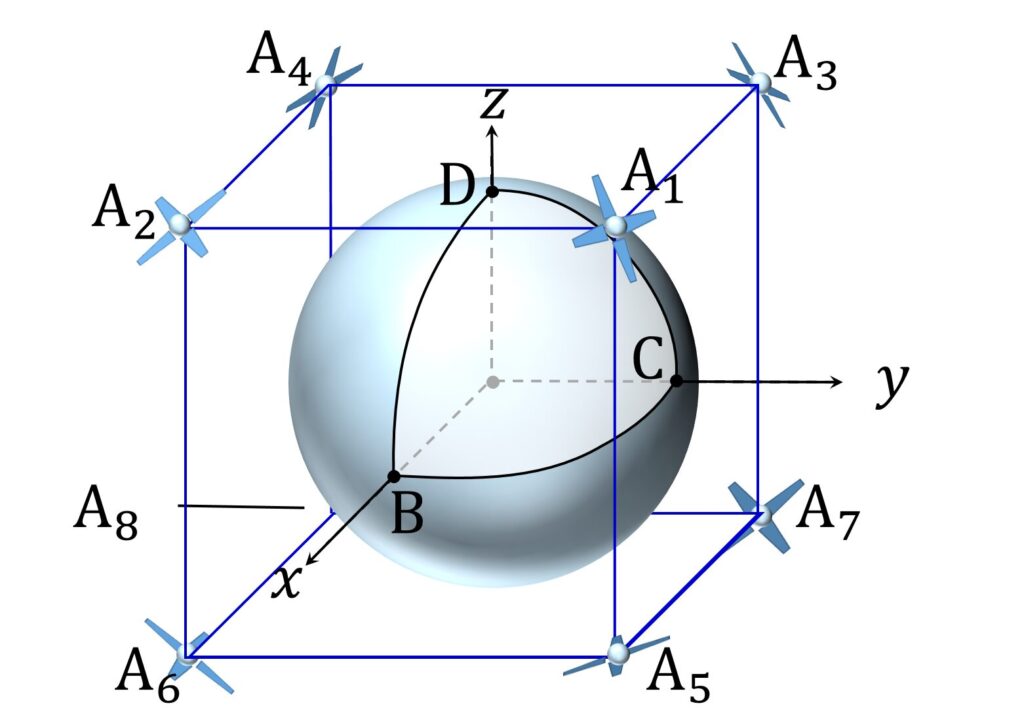
　一方、 A₁ から監視できる球面上の範囲は A₁ から球面に下した接線の足が構成する円の内側です（図3）。

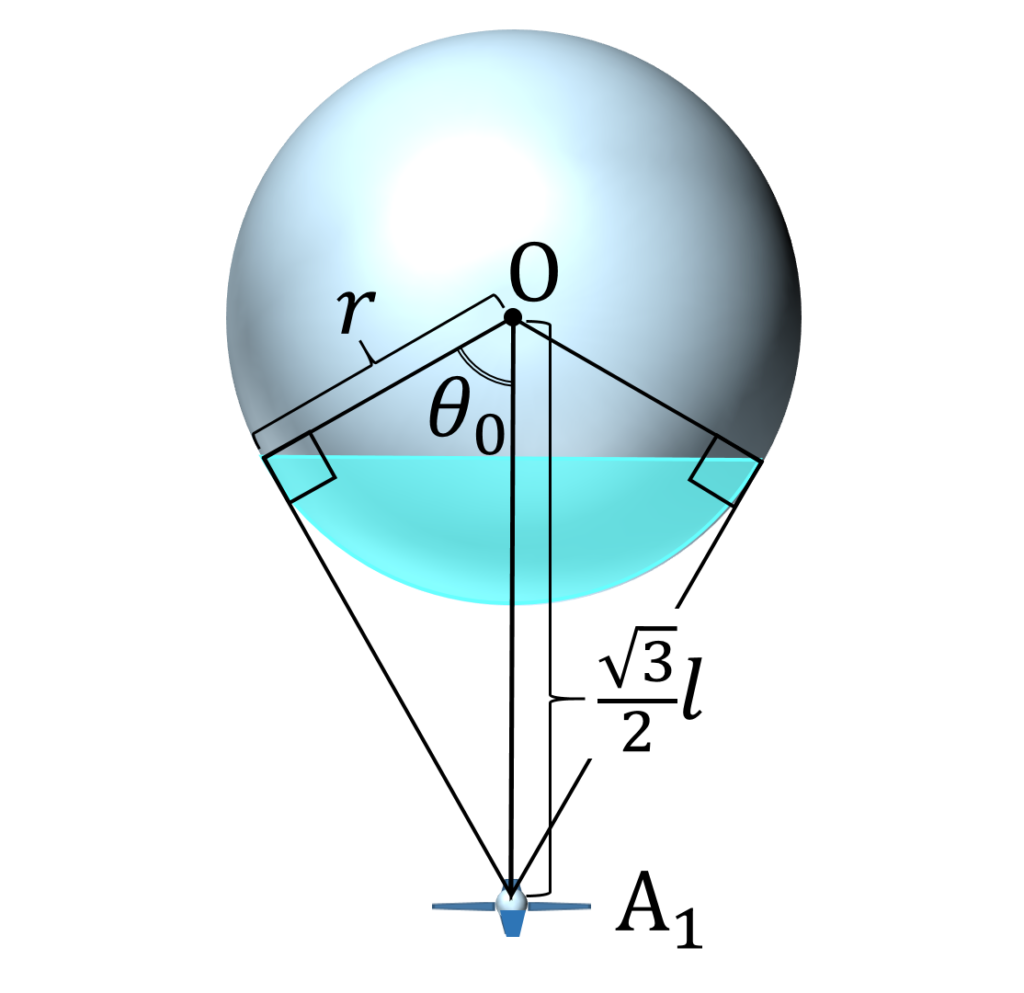
　監視範囲内のすべての点 P において、 OP と OA₁ の成す角をθと置くとき、

\theta \leqq \theta_0

が成り立ちます。ここに θ₀ は

\cos \theta_0 = \frac{2r}{ \sqrt{3}l}

を満たします。なお、以降本稿において角度は0以上π以下の値を取るものとします。

　第1象限が A₁ からすべて監視できるための十分条件は、 A₁ から最も離れた B(r,0,0) 、 C (0,r,0) 、 D(0,0,r) が監視範囲内にあることです。 OB,OC,OD と OA₁ が成す角はすべて等しいのでこれを θ₁ とおくと、 B,C,D が監視範囲内にあるための十分条件は

\theta_1 \leqq \theta_0

すなわち

 \cos\theta_1 \geqq  \cos \theta_0

ですが、

\cos \theta_1 = \frac{ (\overrightarrow{\mathrm{OB}}, \overrightarrow{\mathrm{OA_1}} )}{|| \overrightarrow{\mathrm{OB}} || \cdot ||  \overrightarrow{\mathrm{OA_1}} || } = \frac{ r \cdot \frac{l}2}{r \cdot\frac{ \sqrt{3}}{2 } l} = \frac{1} { \sqrt{3}}

なので、 l ≧ 2r ならば

    \cos \theta_1 =  \frac{1} { \sqrt{3}} \geqq  \frac{2r}{ \sqrt{3}l} = \cos \theta_0 

なので B,C,D が監視範囲内にあるための十分条件が成り立ちます。すなわち A₁ は第一象限全体を監視可能であり、したがって各頂点の監視範囲の総体は球面 S 全体を包含するので、 S 上のすべての点から A₁,A₂, … ,A₈ のうち少なくとも1点が見えます。

　ゆえに S 上のすべての点から A₁,A₂, … ,A₈ のうち少なくとも1点が見えるための必要十分条件は

l \geqq 2r

です。