死角なき難問 – 1996年東大 数学 第3問

2021年7月8日2024年12月9日

小問２の解法

基本的な考え方

　S 上のすべての点から A₁,A₂, … ,A₈ のうち少なくとも2点が見えるということは、全球面上のすべての点において監視範囲が重複しているということです。

　各頂点の監視範囲は一部が隣の象限にはみ出して監視範囲が重複していて、そのような場所からは複数の頂点を見ることが出来ます。

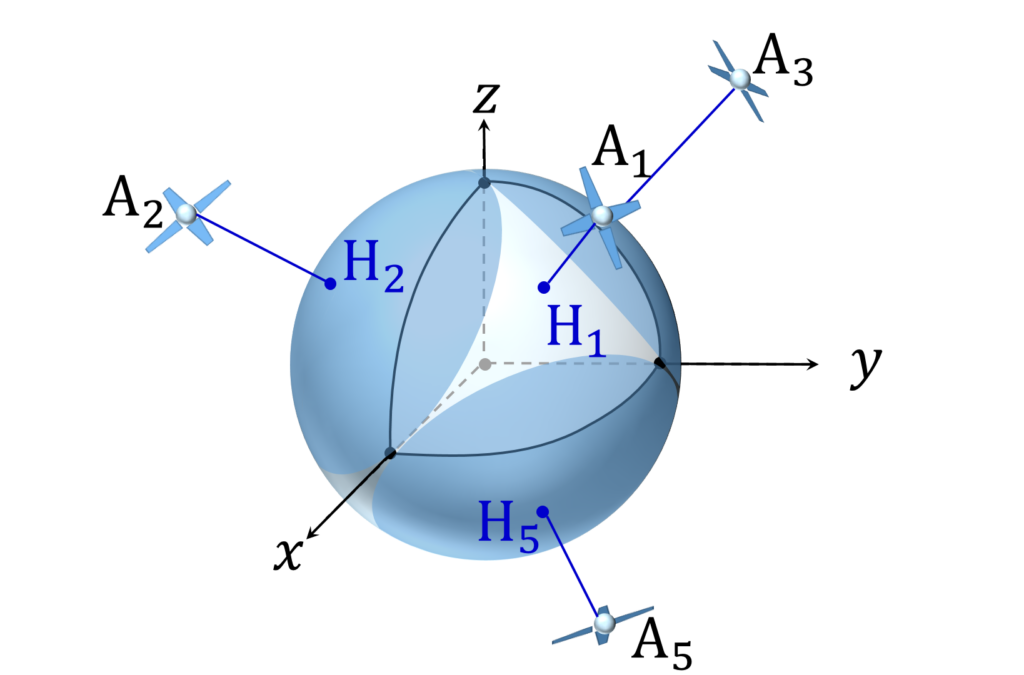
　しかし、 l が「あまり長くない」場合は象限全体を隣接監視範囲からのはみだし部分で網羅しきることはできません。 A₁,A₂, … ,A₈ から S に下した垂線の足（すなわち OA₁,OA₂,…,OA₈ と S の交点）を H₁,H₂,…,H₈ と置くとき、 A₁ の監視範囲が隣接する H₂ や H₃ に届かない場合は隣接頂点からの監視も H₁ に届かないわけですから、 H₁ の近傍では A₁ からしか監視されません(図4の白抜き部分)。

　そこでヤマトを衛星の真下に移動させて直上の衛星を破壊すれば、反射衛星砲からの攻撃は届かなくなります。

　これを防ぐための衛星の高度を求めるのが、小問2の主旨です。

S 上のすべての点から A₁,A₂, … ,A₈ のうち少なくとも2点が見えるための必要条件

　OA₁ と、 A₁ に隣接する頂点 A₂,A₃,A₅ と O とを結ぶ線分 OA₂,OA₃,OA₅ が成す角はすべて等しくて、それを θ₂ とおくとき、 \mathrm{A_1} = (\displaystyle\frac{l}{2},\displaystyle\frac{l}{2},\displaystyle\frac{l}{2}) 、 \mathrm{A_2} = (\displaystyle\frac{l}{2}, -\displaystyle\frac{l}{2},\displaystyle\frac{l}{2}) なので

 \begin{aligned}

\cos \theta_2 =  & \frac{( \overrightarrow{\mathrm{OA_1}},\overrightarrow{\mathrm{OA_2}} )}{|| \overrightarrow{\mathrm{OA_1}} || \cdot ||\overrightarrow{\mathrm{OA_2}} ||} \\
 = & \frac{ \frac{l^2}{4} - \frac{l^2}{4} + \frac{l^2}{4}}{ ( \frac{ \sqrt{3}}{2}l )^2} \\
 = & \frac{1}3

\end{aligned}

が成り立ちます。

　小問1で見たように立方体の1辺の長さ l が与えられたとき、 S 上の点 P がの A₁ の監視範囲であるための必要十分条件は OP と OA₁ の成す角をθと置くとき、

\theta \leqq \theta_0

が成り立つことです。ここに θ₀ は

\cos \theta_0 = \frac{2r}{ \sqrt{3}l}

を満たします。

　 H₂,H₃,H₅ が A₁ から監視できないということは、

 \theta_0 < \theta_2

であることと同値ですが、これは H₁ がA₁ と隣接する A₂,A₃,A₅ から監視できない、すなわちH₁ から一つの頂点 A₁ しか見えないことと同値です。

　つまり θ₀ < θ₂ ならば S 上に頂点が一つしか見えない点が存在するということなので、これの対偶を取ることにより、S 上のすべての点から A₁,A₂, … ,A₈ のうち少なくとも2点が見えるための必要条件は

 \theta_0 \geqq \theta_2

が成り立つことであることがわかりました。

　この必要条件を l を使って表現します。

　 θ₀ ≧ θ₂ ならば

 \cos \theta_0 \leqq \cos \theta_2

が成り立ちます。したがって

 \frac{2r}{ \sqrt{3}l} \leqq \frac{1}3

すなわち

l \geqq 2 \sqrt{3}r

が成り立ちます。ゆえにS 上のすべての点から A₁,A₂, … ,A₈ のうち少なくとも2点が見えるための必要条件は

l \geqq 2 \sqrt{3}r

です。