2011年東工大 数学 第4問 は回転体の体積に関する問題です。問題文は以下の通りです。
平面上に一辺の長さが1の正方形 D および D と交わる直線があるとする。この直線を軸に D を回転して得られる回転体について以下の問いに答えよ。
(1) D と同じ平面上の直線 l は D のどの辺にも平行でないものとする。軸とする直線は l と平行なものの中で考えるとき、回転体の体積を最大にする直線は D と唯1点で交わることを示せ。
(2) D と交わる直線を軸としてできるすべての回転体の体積の中で最大となる値を求めよ。
正方形を回転させるだけなら大したことないようにも思えますが、回転軸がどの辺にも平行でないところがミソです。これのおかげで、計算量が爆発します。「ようこそ計算地獄へ!!」
なお、以下の内容は、東工大が公表したものではありません。
小問1の解法
複数の小問から構成される問題は普通、番号の若い小問のほうが簡単で、後の小問のヒントになっていたりしますが、本問は別で、小問1がメインになっていて難しく、小問2はおまけみたいなものです。
部分点などやる気はサラサラない感全開なので、本番では捨て問確定です。どう解くかよりも、いかに早く見切りをつけるかの方が重要な問題です。東工大の入試は大問が4つしかないので、1問ばっくり捨てるのは勇気がいりますが、ここは他の問題の解答精度を上げることを優先しましょう。
それでは解法の説明に入ります。
回転軸に対する正方形の傾斜角を \theta とおきます。 0 < \theta \leqq \frac{\pi}{4} として一般性を失いません(もし \theta \geqq \frac{\pi}4 なら、反対側の角を \theta とおけばよい)。
問題文では、回転軸の基軸となる直線 l と回転軸を区別していますが、本稿では以降、回転軸それ自体を l と表記します。
また、回転軸から最も遠い頂点と、回転軸との距離を h と置きます(図1)。
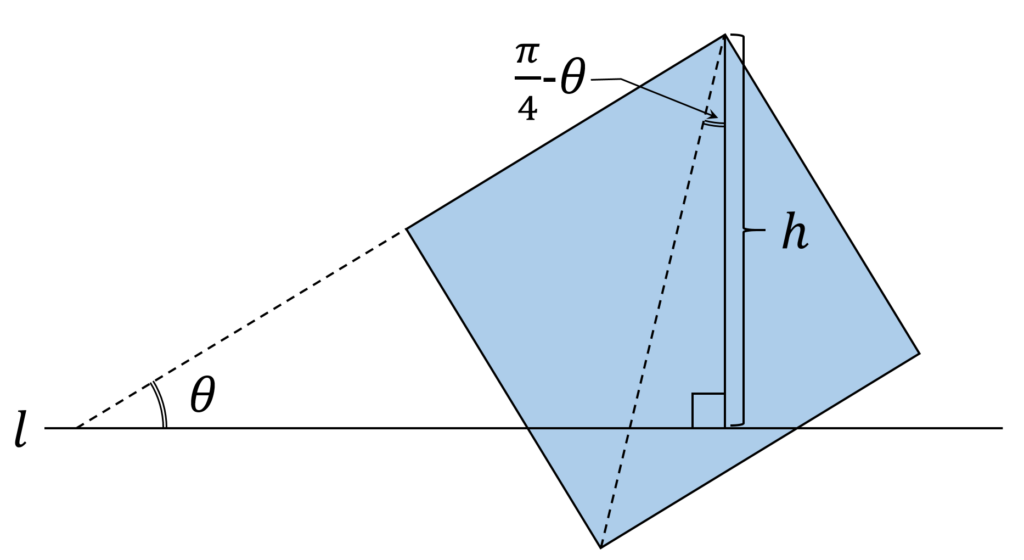
h が最大値をとるのは回転軸が1つの頂点を通る時で、その値は、
\sqrt{2} \cos{( \frac{\pi}{4} - \theta)} = \sin \theta + \cos \thetaとなります。また、 h が最小値をとるのは回転軸が正方形の中心を通る時で、その値は
\frac{1}{2}( \sin \theta + \cos \theta)となります。
\cos \theta \leqq h \leqq \sin \theta + \cos \theta のときの回転させる図形の形状
まず、 \cos \theta \leqq h \leqq \sin \theta + \cos \theta の場合を考えます。このとき、正方形の頂点のうち3つが回転軸の片側に、もう1つがその反対側に来ます(図2)。
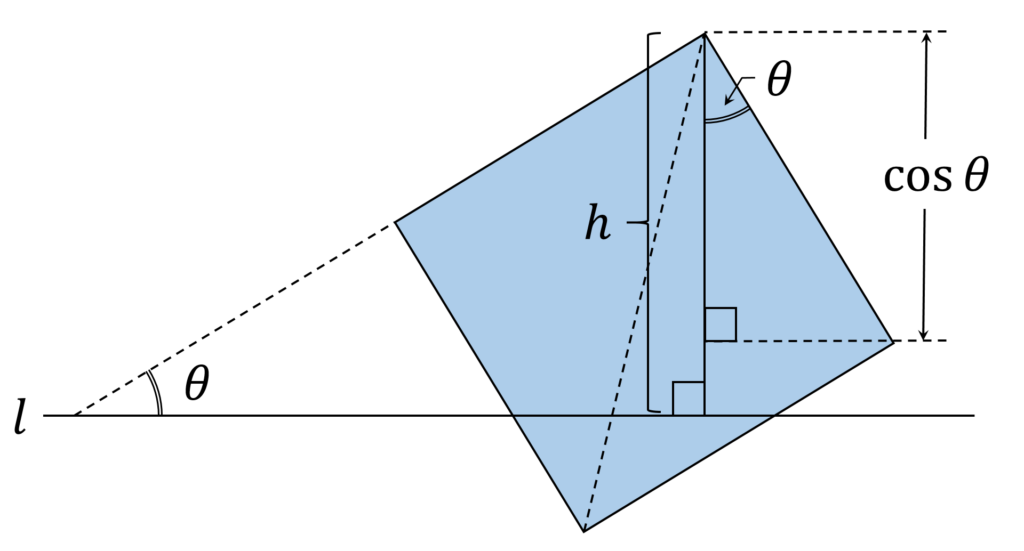
正方形を回転軸に沿って回転させたときに、下側の三角形が上側の大きいほうの図形に含まれていることを確認します。
図形の頂点等に、図3のように記号を振ります。
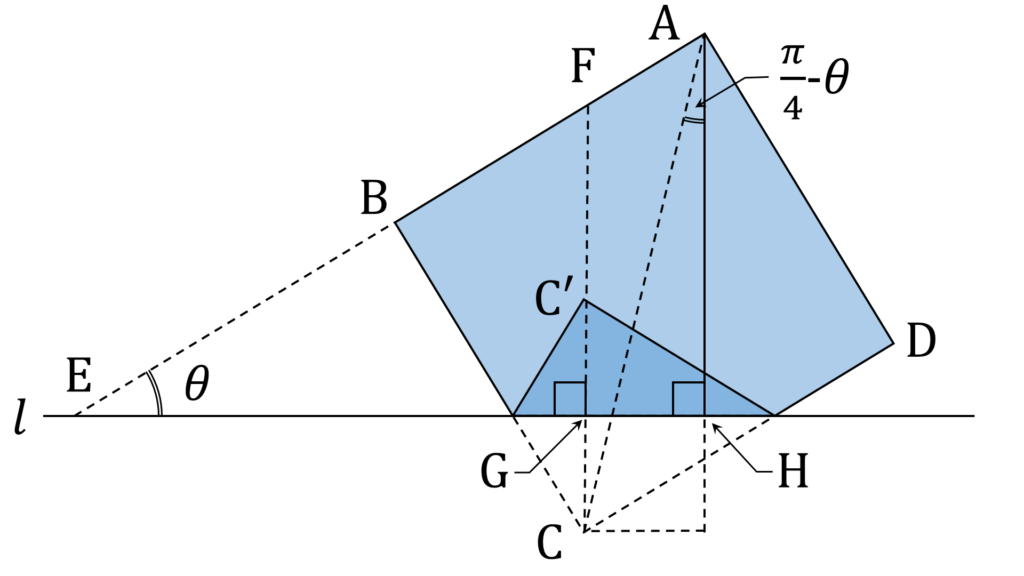
このとき、各線分の長さは以下の通りです。
\begin{aligned}
& \mathrm{AH} = h \\
& \mathrm{EH} = h \cot \theta \\
& \mathrm{GH} = \sqrt{2} \sin(\frac{\pi}{4} - \theta) \\
& \text{ } = \cos \theta - \sin \theta \\
& \mathrm{CF} = \frac{1}{\cos \theta}
\end{aligned}ここで、FG と \mathrm{C'G} の長さを求めます。
\frac{\mathrm{FG}}{ \mathrm{AH}} = \frac{ \mathrm{EH} - \mathrm{GH}} { \mathrm{EH}}なので、
\mathrm{FG} = h -\sin \theta + \frac{\sin^2\theta}{\cos \theta}となります。また、
\begin{aligned}
&\mathrm{C'G} = \mathrm{CF} - \mathrm{FG} \\
& =\frac{1}{\cos \theta} - (h -\sin \theta + \frac{\sin^2\theta}{\cos \theta}) \\
& = -h + \sin \theta + \cos \theta
\end{aligned}となります。
FG と \mathrm{C'G} の長さを比較します。
\begin{aligned}
& \mathrm{FG} - \mathrm{C'G} \\
& = h -\sin \theta + \frac{\sin^2\theta}{\cos \theta} \\
&- (-h + \sin \theta + \cos \theta) \\
& = 2h- 2\sin \theta -\cos \theta+ \frac{\sin^2 \theta}{\cos \theta} \\
& \geqq 2 \cos \theta - 2\sin \theta -\cos \theta+ \frac{\sin^2 \theta}{\cos \theta} \\
& = \cos \theta - 2\sin \theta + \frac{\sin^2 \theta}{\cos \theta} \\
& = \frac{1}{\cos \theta} - 2\sin \theta \\
& = \frac{1- 2 \sin \theta \cos \theta}{\cos \theta} \\
& = \frac{1- \sin 2\theta}{\cos \theta} \geqq 0
\end{aligned}なので、FG のほうが \mathrm{C'G} より長いか等しく、 したがって下側の三角形が上側の大きいほうの図形に含まれていることが示せました。
\cos \theta \leqq h \leqq \sin \theta + \cos \theta のときの回転体の体積を円錐の組み合わせで求める
これまでの考察により、回転させる図形の形状は図4の通りです。
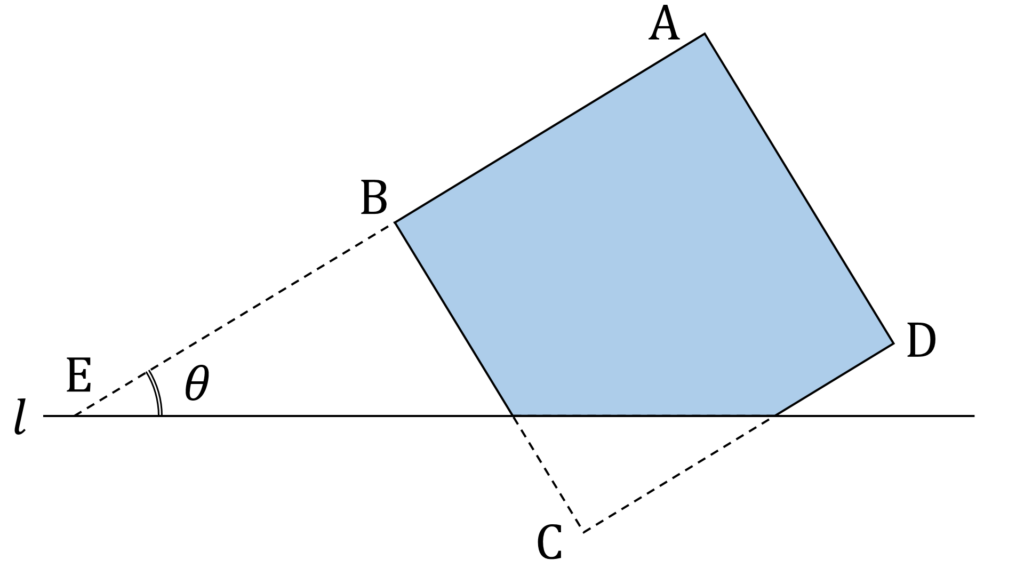
体積の求め方としては、 y = f(x) を x 軸の周りに回転させてできる図形の体積の公式
\pi\int_a^b f^2(x) dx
を適用することが最初に思いつきますが、本問は f(x) が複雑すぎて、計算が泥沼に陥りそうなので、もっと手軽に求めることを考えます。
よく考えてみると、体積を求めたい立体は円錐の合成になっていて、しかもその円錐は、相似なものを同一視すると「左向き」と「右向き」の2種類しかありません。
そこで、図5のもとに、各円錐を以下のように定義します。
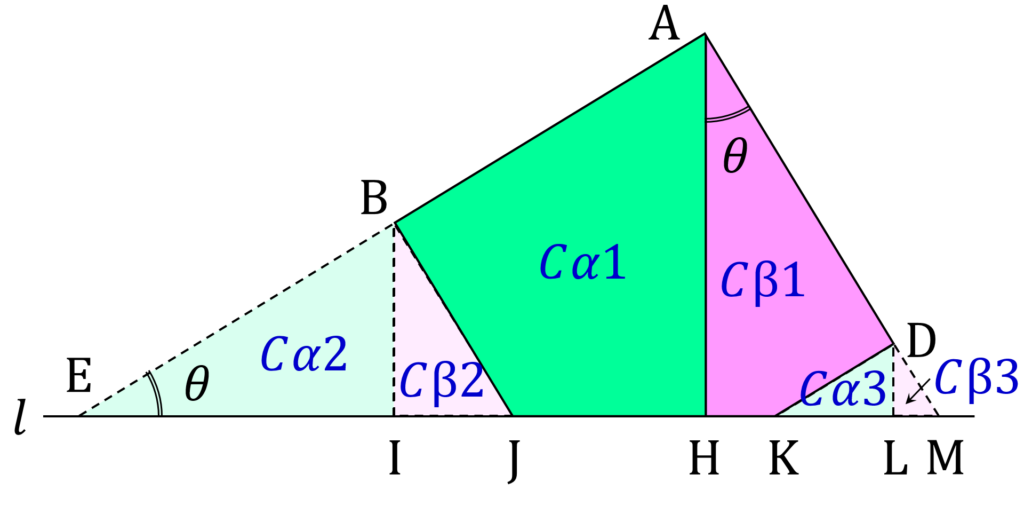
| 名称 | 説明 | 相似関係 |
|---|---|---|
| C \alpha 1 | △AEH を回転させてできる円錐 | |
| C \alpha 2 | △BEI を回転させてできる円錐 | C \alpha 1 と相似 |
| C \alpha 3 | △DKL を回転させてできる円錐 | C \alpha 1 と相似 |
| C \beta 1 | △AMH を回転させてできる円錐 | |
| C \beta 2 | △BJI を回転させてできる円錐 | C \beta 1 と相似 |
| C \beta 3 | △DML を回転させてできる円錐 | C \beta 1 と相似 |
このとき、求める体積 V は、
\begin{aligned}
& V = C\alpha1 + C\beta1\\
& \text{ } - C \alpha2 -C\beta2 \\
& \text{ }-C \alpha3 -C \beta 3
\end{aligned}と表せます。ここで各円錐の体積を、その名称で表現しています。
円錐の相似比
相似な円錐の体積は相似比を求めることで、少ない計算で体積を算出することが出来ます。
\begin{aligned}
& \frac{\mathrm{BI}}{\mathrm{AH}} = \frac{\mathrm{BE}}{\mathrm{AE}} = \frac{ \mathrm{AE}-1} {\mathrm{AE} } \\
& \frac{\mathrm{DL}}{\mathrm{AH}} = \frac{\mathrm{DM}}{\mathrm{AM} }= \frac{\mathrm{AM}-1} {\mathrm{AM} } \\
\end{aligned}なので、
\begin{aligned}
& \mathrm{BI} = h-\sin \theta \\
& \mathrm{DL}= h - \cos \theta \\
\end{aligned}となります。
ゆえに各円錐の相似比は、以下の通りです。
\begin{aligned}
& C \alpha1 : C \alpha2 = \mathrm{AH} : \mathrm{BI} = h :(
h -\sin \theta ) \\
& C \alpha1 : C \alpha3 = \mathrm{AH} : \mathrm{DL} = h :(
h -\cos \theta ) \\
& C \beta 1 : C \beta2 = \mathrm{AH} : \mathrm{BI} = h :(
h -\sin \theta ) \\
& C \beta1 : C \beta3 = \mathrm{AH} : \mathrm{DL} = h :(
h -\cos \theta ) \\
\end{aligned}回転体の体積を算出する
体積比は相似比の3乗なので、
\begin{aligned}
& C \alpha2 = \left ( \frac{h -\sin \theta}{h} \right )^3 C \alpha1 \\
& C \alpha3 = \left ( \frac{h -\cos \theta}{h} \right )^3 C \alpha1 \\
& C \beta2 = \left ( \frac{h -\sin \theta}{h} \right )^3 C \beta1 \\
& C \beta3 = \left ( \frac{h -\cos \theta}{h} \right )^3 C \beta1 \\
\end{aligned}です。また、
\begin{aligned}
& C \alpha 1 = \frac{\pi}{3} h^3 \cot \theta \\
& C \beta 1 = \frac{\pi}{3} h^3 \tan \theta \\
\end{aligned}なので、求める体積 V は
\begin{aligned}
& V = C\alpha1 + C\beta1 \\
& \text{ } - C \alpha2 -C\beta2 \\
& \text{ } -C \alpha3 -C \beta 3 \\
& = C\alpha1 + C\beta1 \\
& - \left ( \frac{h -\sin \theta}{h} \right )^3 C \alpha1 - \left ( \frac{h -\cos \theta}{h} \right )^3 C \alpha1 \\
&- \left ( \frac{h -\sin \theta}{h} \right )^3 C \beta1 - \left ( \frac{h -\cos \theta}{h} \right )^3 C \beta1 \\
& = (C\alpha1 + C\beta1) \\
& \times \left \{1 -\left ( \frac{h -\sin \theta}{h} \right )^3 - \left ( \frac{h -\cos \theta}{h} \right )^3 \right \}\\
&= \frac{\pi\{ h^3 - (h -\sin \theta)^3 - (h -\cos \theta)^3\}}{3\sin \theta \cos \theta}
\end{aligned}となります。
回転体の体積の最大値
V を h で微分します。
\begin{aligned}
& \frac{dV}{dh} \\
&= \frac{3\pi \{ h^2 - (h -\sin \theta)^2 - (h -\cos \theta)^2\}}{3\sin \theta \cos \theta} \\
& = \frac{\pi [ -\{h - ( \sin \theta + \cos \theta )\}^2 + 2 \sin \theta \cos \theta ]}{\sin \theta \cos \theta}
\end{aligned}となりますが、 \frac{dV}{dh} は \cos \theta \leqq h \leqq \sin \theta + \cos \theta の範囲で正なので、 V はこの範囲で単調増加です。
したがって、 V は h = \sin\theta + \cos \theta のときに最大値
\begin{aligned}
& \frac{\pi \{ (\sin \theta + \cos \theta)^3 - \sin^3 \theta - \cos^3 \theta\}}{3\sin \theta \cos \theta} \\
& = \pi(\sin \theta + \cos \theta)
\end{aligned}をとります。
このとき、回転軸は正方形 D と頂点 C の1点でのみ交わります。
(\sin \theta + \cos \theta) / 2 \leqq h < \cos \theta のときの回転させる図形の形状
次に、回転軸をはさんで正方形の頂点が2つずつに分かれる場合です。この場合、回転させる図形の形状がかなり複雑になります(図6)。
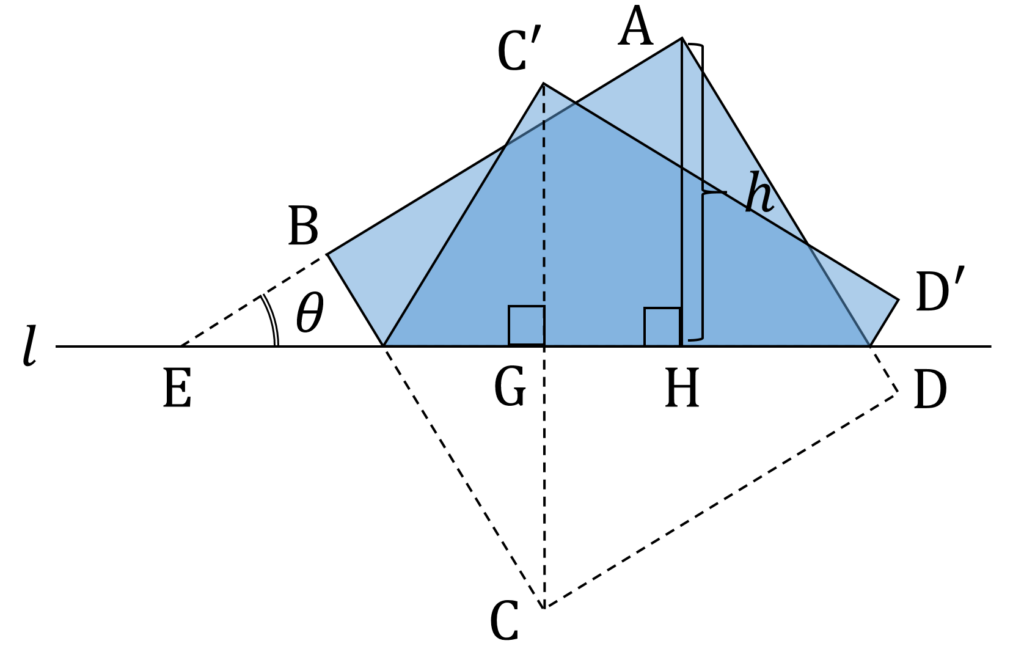
先ほどのように円錐の足し引きで体積を求めるというのも、かなり大変そうなので、別のアプローチをさぐります。
示したいのは回転体の体積がさっき計算した \pi(\sin \theta + \cos \theta) 以下になることであって、正確な体積ではありません。そこで、回転体がもっと単純な形状の図形(例えば円柱とか)に包含され、それが最大値より小さくなることを示します。
ところで、上の方で示したように
\begin{aligned}
&\mathrm{C'G} = -h + \sin \theta + \cos \theta \\
\end{aligned}ですが、 (\sin \theta + \cos \theta) /2 \leqq h であることに注意すると、
\begin{aligned}
&\mathrm{C'G} = -h + \sin \theta + \cos \theta \\
& \text{ } \leqq -h + 2h = h = \mathrm{AH} \\
\end{aligned}が成り立つので、回転体の体積は、底面の半径が h 、高さが
\begin{aligned}
& \mathrm{BD} \cos (\frac{\pi}{4} - \theta)\\
& =\sqrt{2} \cos (\frac{\pi}{4} - \theta) \\
&= \sin \theta + \cos \theta
\end{aligned}の円柱に含まれます(図7)。
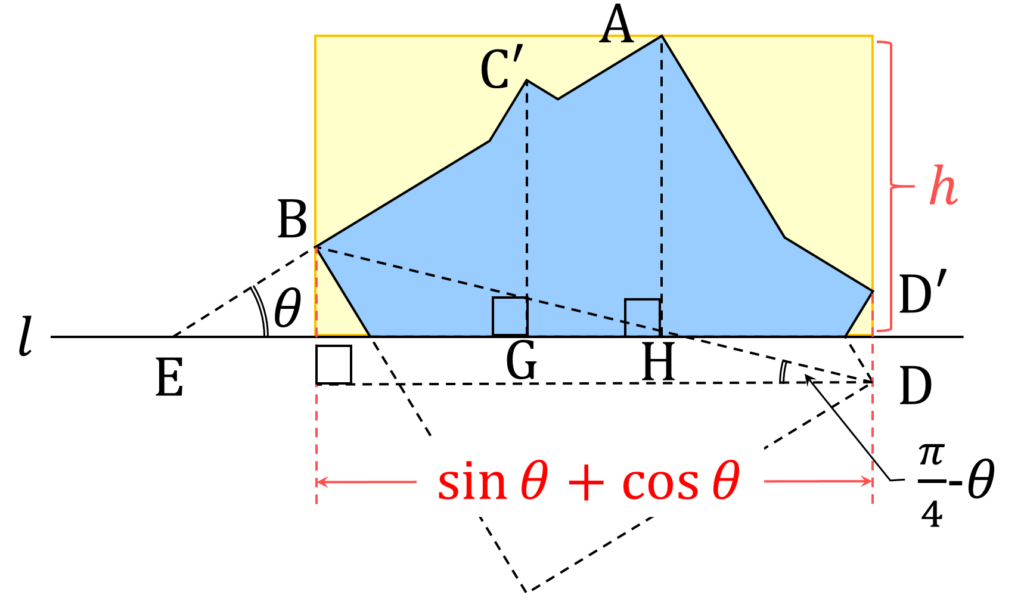
円柱の体積は
\pi h^2(\sin \theta + \cos \theta)
ですが、
\begin{aligned}
& \pi h^2(\sin \theta + \cos \theta) \\
& < \pi \cos^2 \theta(\sin \theta + \cos \theta) \\
& < \pi (\sin \theta + \cos \theta)
\end{aligned}となるので、回転体の体積は \pi(\sin \theta + \cos \theta) より小さいことが示せました。
ゆえに、回転体の体積は回転軸が正方形 D の1つの頂点を通る時に最大になり、その時の体積は
\pi (\sin \theta + \cos \theta)
です。
小問2の解法
小問1に比べると、小問2は拍子抜けするくらい簡単です。
\pi (\sin \theta + \cos \theta)= \sqrt{2} \pi \cos (\frac{\pi}{4} - \theta)であることと、 \theta の範囲が 0 <\theta \leqq \frac{\pi}{4} であることから、回転体の体積は \theta = \frac{\pi}{4} のときに、最大値 \sqrt{2} \pi をとります。
解法のポイントと今後の学習方針

本問は回転させる図形が複雑なので、計算ミスをしないよう気を付けることが大切です。
本稿では円錐の体積と相似比を使うことで計算量を削減しましたが、それでも場合分けが有ったりして、とにかく計算が大変です。
時間がないときは、正方形の頂点が回転軸をはさんで2つずつに分かれる (\sin \theta + \cos \theta) / 2 \leqq h < \cos \theta のケースを、とぼけてすっ飛ばしてしまっても最大値は算出できるので、ある程度の点数はもらえるかもしれません。
今後の学習方針としては、微積分や三角関数に関する計算問題を大量に解いて、計算力をつけることに尽きるでしょう。
