2020年東大 数学 第2問 も、どうすればいいかすぐには思いつかない問題です。取り付く島の無さでは、同じ2020年の第4問をしのぎます。
問題文は以下の通りです。
平面上の P,Q,R が同一直線状にないとき、それらを頂点とする三角形の面積を △PQR で表す。また、 P,Q,R が同一直線状にあるときは、 △PQR=0 とする。
A,B,C を平面上の3点とし、 △ABC=1 とする。この平面上の点 X が
2 ≦ △ABX + △BCX + △CAX ≦ 3
を満たしながら動くとき、 X の動きうる範囲の面積を求めよ。
第4問が強敵なので、本問をおいそれと捨ててしまうわけにはいきませんが、本番ではとりあえず5分間にらんでみて、打開策を思いつかなければ後回しにしましょう。
2020年東大 数学 第2問 の解法
点 X が △ABC の内側にある時は、 △ABX + △BCX + △CAX = 1 なので、点 X が △ABC の外側にある場合だけを考えればよいことがわかります。
試行錯誤
セオリーに従って図を書いてみますが、 △ABC が具体的に与えられていないこともあって、さっぱりイメージが湧きません。
それではということで、点 X を任意に動かすというところから、座標系を導入して代数的に攻めてみますが、点 X から各辺へ垂らした垂線の長さを求めるところで、計算量が膨大になって筆者は嫌になってしまいました。
そもそも、 X の動きうる範囲の面積と言っているので、おそらく具体的な形状を求める必要があるでしょうし、代数的なアプローチは抽象的過ぎて、無理そうです。
ここまでの考察に5分以上かかったら、ちょっと厳しくなります。とりあえず後回しにして、第4問の2のべき乗泥沼にダイブしましょう。
図形描画アプローチに回帰する
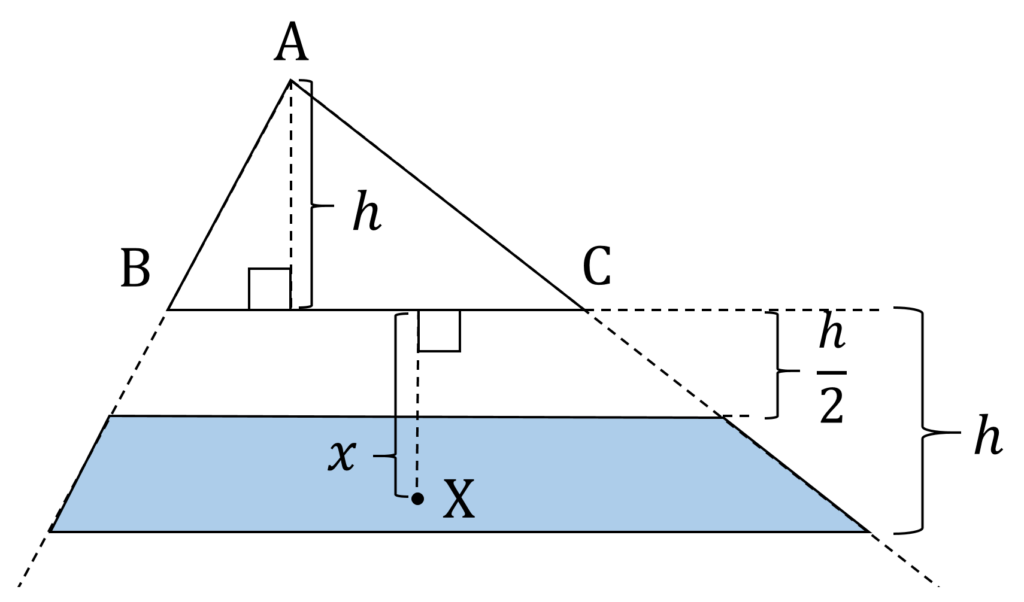
求める図形は、 △ABC をぐるりとドーナツ状に取り囲んでいそうな気がしますが、どんな形か予想がつきません。 △ABC の内側が対象外なのはわかっていますので、その外側のみを考えればよいのですが、まずは辺 BC をはさんで頂点 A と反対側で、かつ BC の幅の範囲でBCに垂直な方向に限定して、考えてみます(図1)。
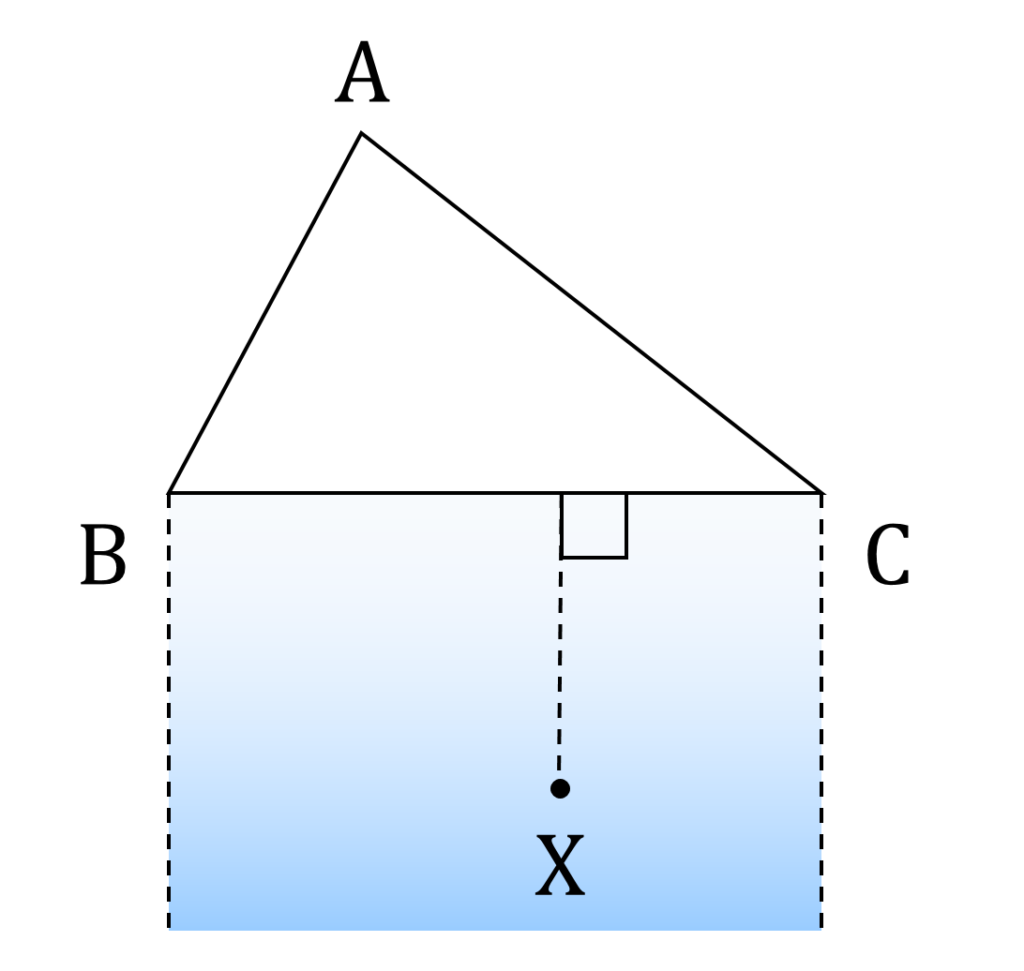
辺BCをはさんで頂点Aと反対側に関する考察
このとき、
△ABX + △CAX
= △ABC + △BCX
= 1 + △BCX
なので、
△ABX + △BCX + △CAX
= 1 + 2△BCX
・・・(1)
が成り立ちます(図2)。
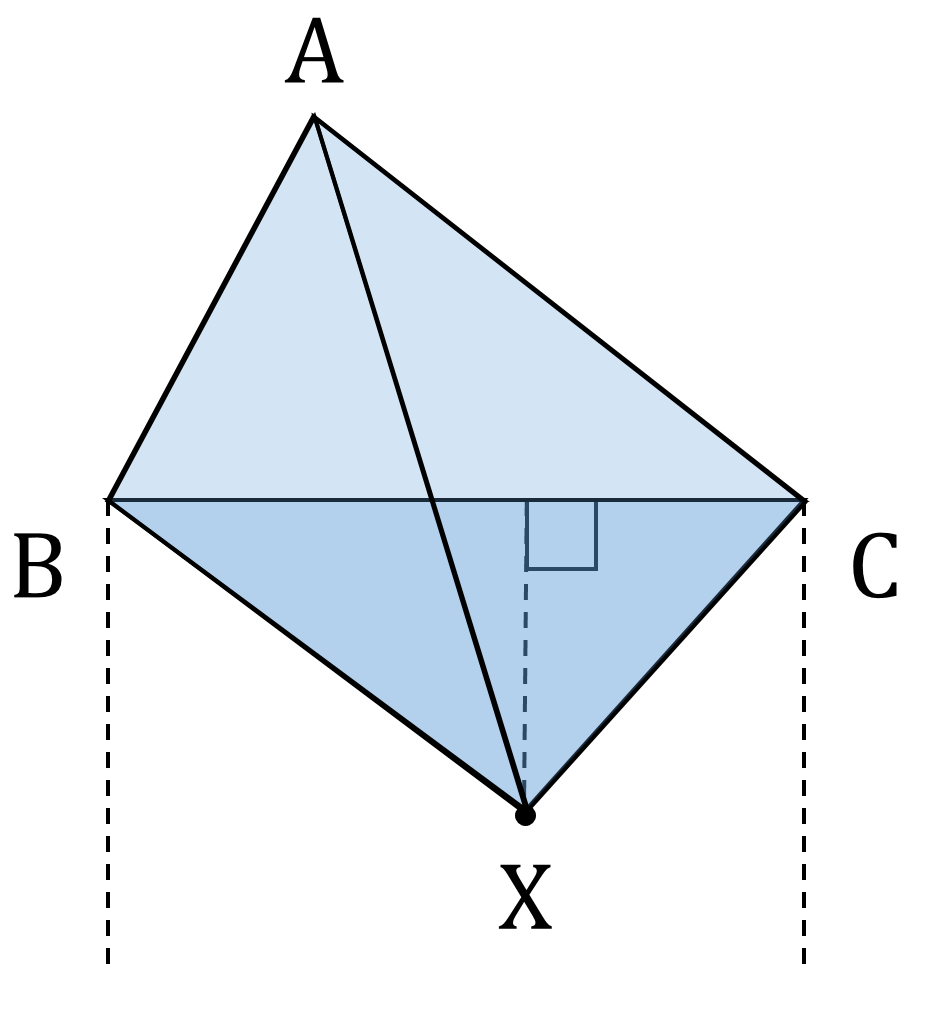
△BCX は点 X と辺 BC の距離で表せるので、△ABX + △BCX + △CAX も同様です。これに気が付ければ、本問の峠は越えました!
面積を点 X と辺 BC の距離で表す
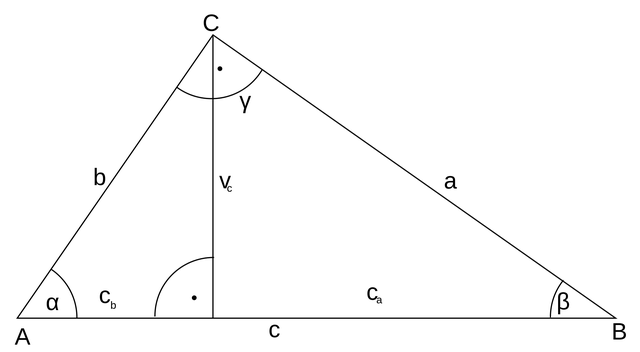
ここで記号の準備です。辺 AB の長さを a 、頂点 A から辺 BC に垂らした垂線の長さを h 、点 X から辺 BC に垂らした垂線の長さを x とおきます。このとき、
\triangle \mathrm{ABC} = \frac{1}{2} ah = 1です。
また、
S = \triangle \mathrm{ABC} + \triangle \mathrm{BCX} + \triangle \mathrm{CAX}とおきます。このとき、式(1)から
S = 1 +2 \triangle \mathrm{BCX} = 1+axが導出できます。
ところが 2 \leqq S \leqq 3 なので、
2 \leqq 1+ax \leqq 3
です。したがって
1 \leqq ax \leqq 2
です。さらに、 \frac{1}{2} ah = 1 であったので a = \frac{2}{h} です。これを上の不等式に代入して
1 \leqq \frac{2x}{h}\leqq 2です。よって
\frac{h}{2} \leqq x\leqq hを得ます。すなわち、 2 \leqq S \leqq 3 となる X の範囲は以下の図3の通りです。
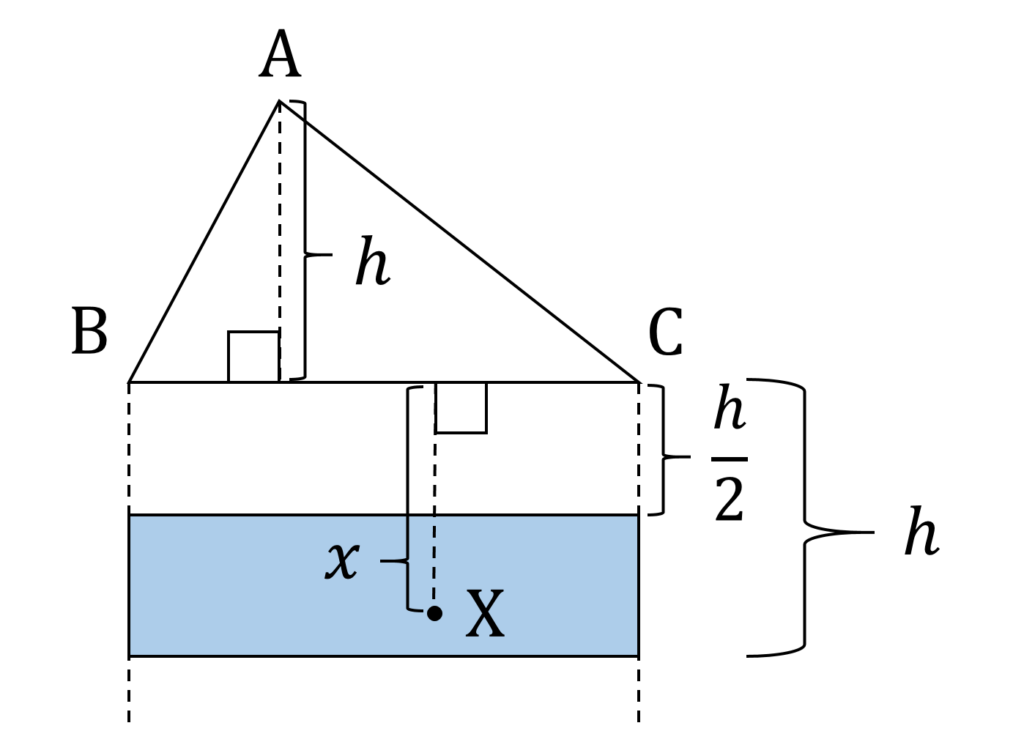
点Xの可動範囲を広げる
ところでよく考えてみると、これまでの考察は X が辺 AB の延長線および辺 AC の延長線の内側にあれば、同じように成り立ちます(図4)。
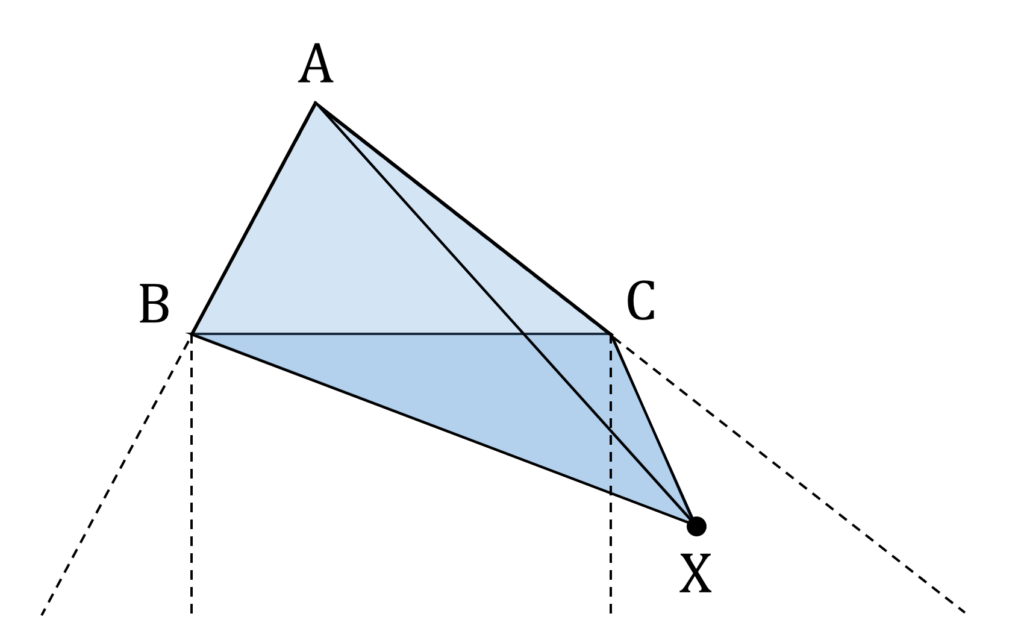
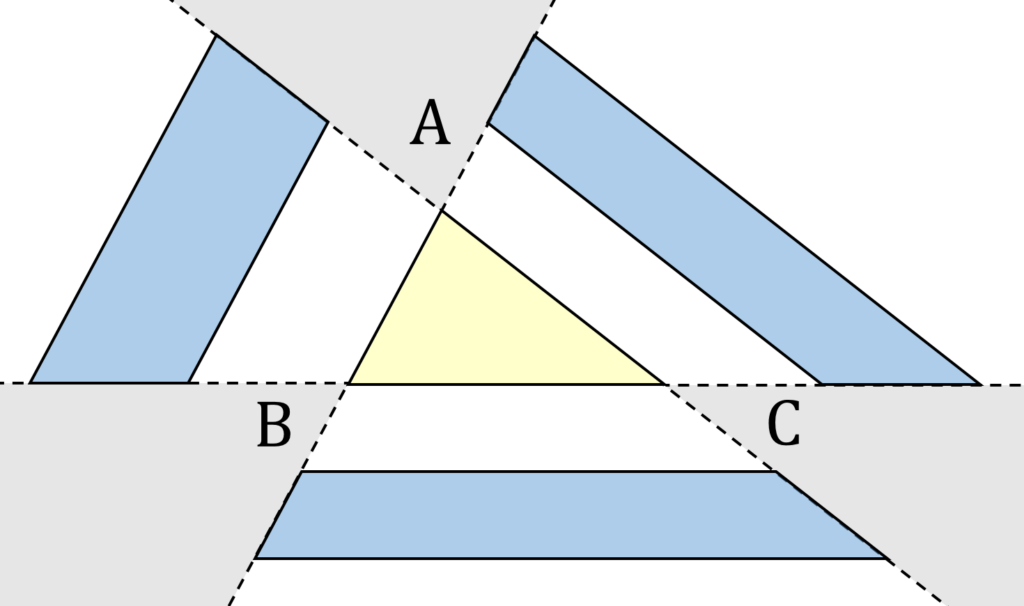
この気付きにしたがって、 2 \leqq S \leqq 3 となる X の範囲を見直すと、以下の図5のようになります。
この領域の面積は容易に計算できて、台形の上底が \frac{3}{2}a 、下底が 2a 、高さが \frac{1}{2}h なので
\begin{aligned}
& (\frac{3}{2}a + 2a) \times \frac{1}{2}h \div 2 \\
& = \frac{7}{8}ah = \frac{7}{4}
\end{aligned}となります。
同じような領域が △ABC のまわりに3つあるので、それらの面積の合計は
\frac{7}4 \times 3 =\frac{21}4となります(図6)。
辺BCから見て頂点Aと同じ側に関する考察
残りは図6のグレーの部分です。3つありますが、代表して頂点 A を中心に考察します。
辺 AB 、辺 AC を辺 BC と反対方向に延長し、それらの半直線に挟まれる領域に点 X を置きます。このとき、
△ABX + △CAX + △ABC = △BCX
が成り立つので、
△ABX + △CAX + △BCX
= 2△BCX – △ABC
= 2△BCX – 1
が成り立ちます。したがって、
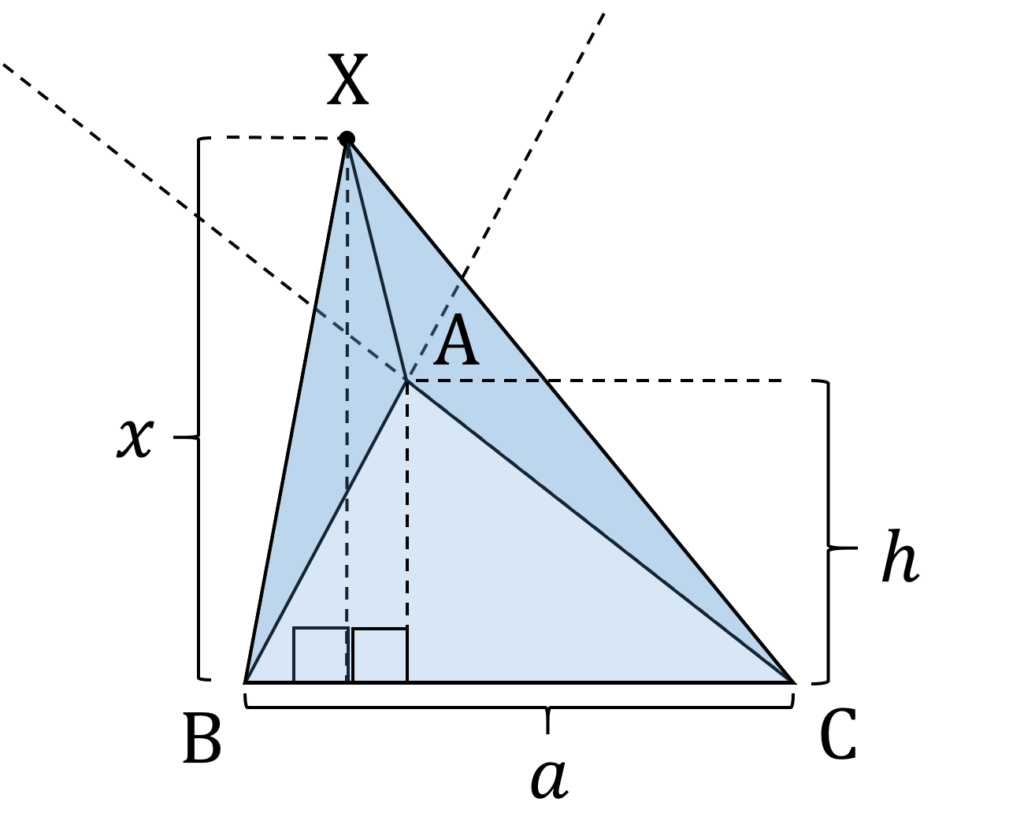
S = ax -1
を得ます(図7)。
2 \leqq S \leqq 3 なので、
2 \leqq ax -1 \leqq 3
したがって
3 \leqq ax \leqq 4
\frac{1}{2} ah = 1 なので
\frac{3}{2} h \leqq x \leqq 2hを得ます。 h がこの範囲の領域で 2 \leqq S \leqq 3 が成り立ちますが、その面積は
\frac{3}{4} です(図8)。
これまでの結果を合計して求める面積を算出する
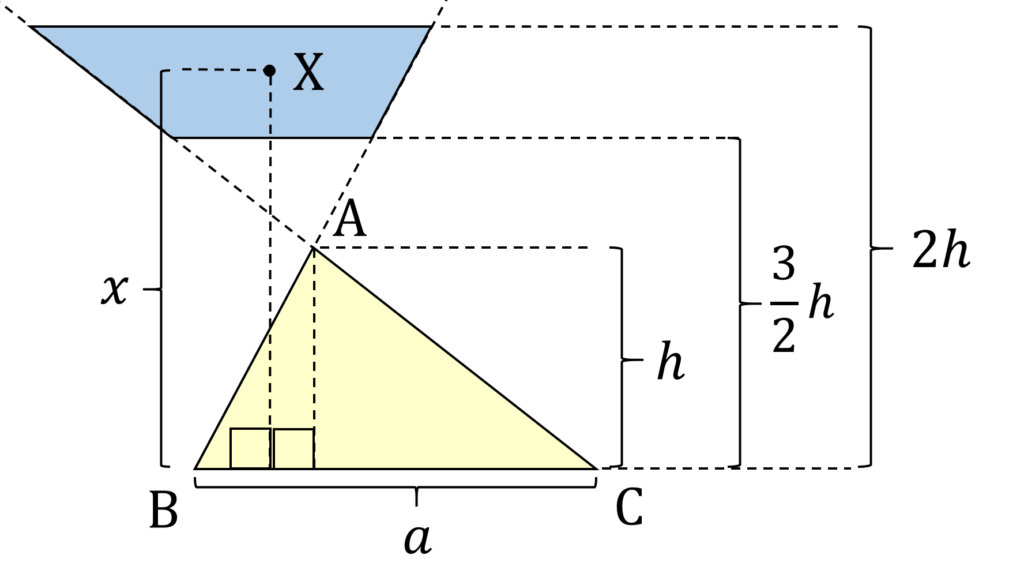
同じような領域が △ABC のまわりに3つあるので、それらの面積の合計は
\frac{3}4 \times 3 =\frac{9}4ゆえに、求める面積は
\frac{21}4 + \frac{9}4 =\frac{15}2となります(図9)。
解法のポイント
一見、非常に難解な本問ですが、使った数学は相似比と、あとは台形の面積公式くらいです。数学的センスのみを純粋に問う設問になっています。
本問は図2や図7を描いて △ABX + △CAX + △ABC をどのように計算するかをイメージできるかどうかがポイントです。点 X から各辺に垂線を垂らしてその長さからどうたらこうたら、みたいな議論に落ち込むと、正解にたどり着けません。
最初から汎用的なロジックを構成しようとするのではなく、本稿で示したように特殊かつ限定的な範囲で考察して、問題をより単純化すると正解に近づけるでしょう。
