1998年東大 数学 第2問 は格子点の個数に関する問題です。問題文は以下の通りです。
n を正の整数とする。連立不等式
\left \{
\begin{aligned}
x + y + z & \leqq n \\
-x + y - z & \leqq n \\
x - y - z & \leqq n \\
-x - y + z & \leqq n \\
\end{aligned}
\right .
を満たす xyz 空間の点 P (x,y,z) で、 x,y,z がすべて整数であるものの個数を f(n) とおく。極限 \lim\limits_{n \rightarrow \infty} \frac{f(n)}{n^3} を求めよ。
東大入試の1998年数学は、後期第3問は別格としても、前期の第3問、第4問のような難問が立て続けに屹立していますが、本問もそれらに負けず劣らず、最凶レベルの訳わからんちん度を誇っています。
捨て問スルーしようとしても、前門の第3問、後門の第4問と言った感じで、もうどこにも逃げ道はありません。腹を据えて取り組むしかないようです。
1998年東大 数学 第2問 の解法
図形のイメージを把握する
まず、設問が言っている領域がどんな形なのか、把握します。一見したところ、無限の領域のような気がしますが、設問の内容は有限の領域であることを示唆しています。
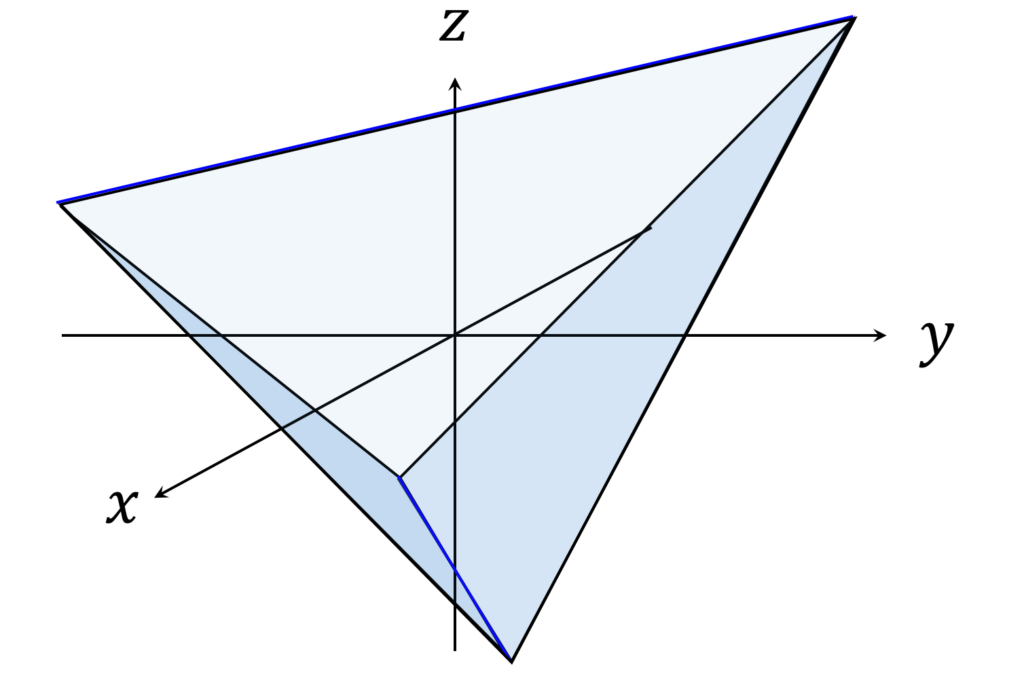
となると4平面で構成されるのだから四面体か?しかも変数の対称性から見てどの面も同じ形と大きさの正四面体ではないか?と予測できます。
ある程度あたりをつけたところで、図を書いてみます。
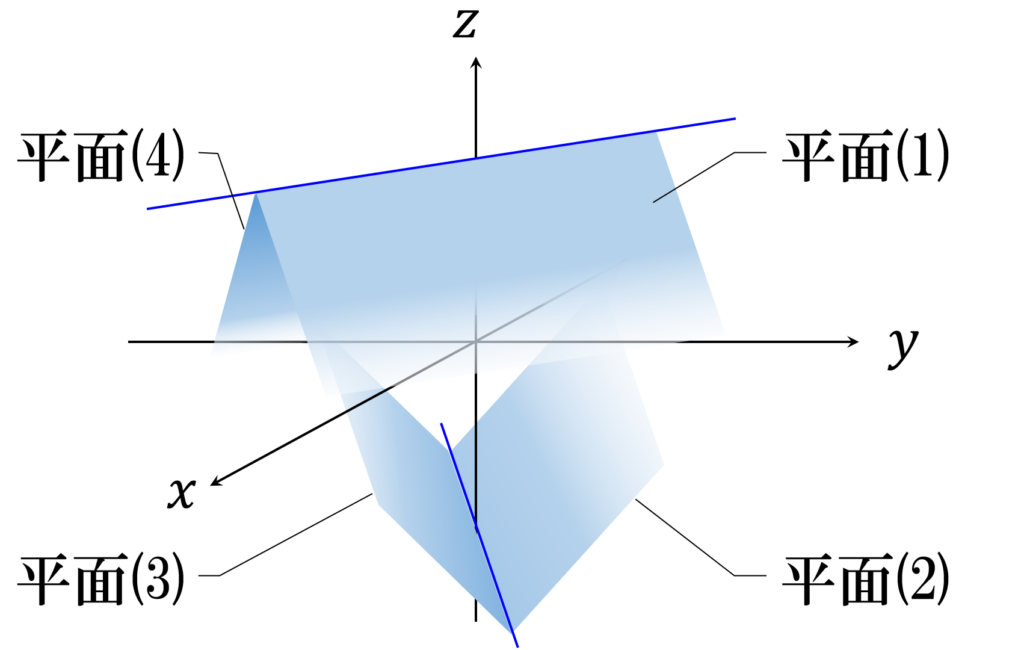
設問の連立不等式を構成する平面に、以下のように番号を振ります。
\begin{aligned}
x + y + z & = n \cdots(1) \\
-x + y - z &= n \cdots (2)\\
\text{ }x - y - z &= n \cdots (3) \\
-x - y + z &= n \cdots (4) \\
\end{aligned}すると、平面(1) と平面(4) の交線の方程式は
x+y=0, z=n
平面(2) と平面(3) の交線の方程式は
-x+y=0, z=-n
となり、それぞれの交線は xy 平面と平行で、かつ直角方向にねじれていることがわかります(図1)。
よって対象の図形のイメージは以下のようになります(図2)。
格子点の数を数え上げる
①図形の表面の格子点をカウントし、隣接項差分式の和で全数を求める
図形のイメージがつかめたところで、格子点の数をカウントする作業に入ります。
とはいうものの面倒くさそうだと気が引ける一方で、 f(n) -f(n-1) は図形の表面の格子点の数であることに着目します。
この事実は明らかだと思いますが、念のため確認しておきます。
自然数 n に対し、 F_n を設問の不等式を満たす領域であるとし、また、 S_n を、 F_n に含まれる格子点の集合とするとき、格子点 (x,y,z) \in \mathbb{Z}^3 が (x,y,z) \notin S_{n-1} である必要十分条件は
\begin{aligned}
x + y + z & > n-1 \\
-x + y - z & > n-1 \\
x - y - z & > n-1\\
-x - y + z & > n-1 \\
\end{aligned}
のいずれかが成り立つことです。したがって、 (x,y,z) \in S_n \setminus S_{n-1} である必要十分条件は
\left \{
\begin{aligned}
x + y + z & \leqq n \\
-x + y - z & \leqq n \\
x - y - z & \leqq n \\
-x - y + z & \leqq n \\
\end{aligned}
\right .かつ
\begin{aligned}
x + y + z & = n \\
-x + y - z & = n \\
x - y - z & = n\\
-x - y + z & = n \\
\end{aligned}
\text{ のいずれか}
が成り立つことですが、これは (x,y,z) が F_n の表面に存在していることを意味しています。
そこで、とりあえず表面の格子点の数を数え上げ、しかる後に隣接項差分式の和をとることで、図形に含まれる格子点の数を求めることにします。
② xy 平面上の格子点
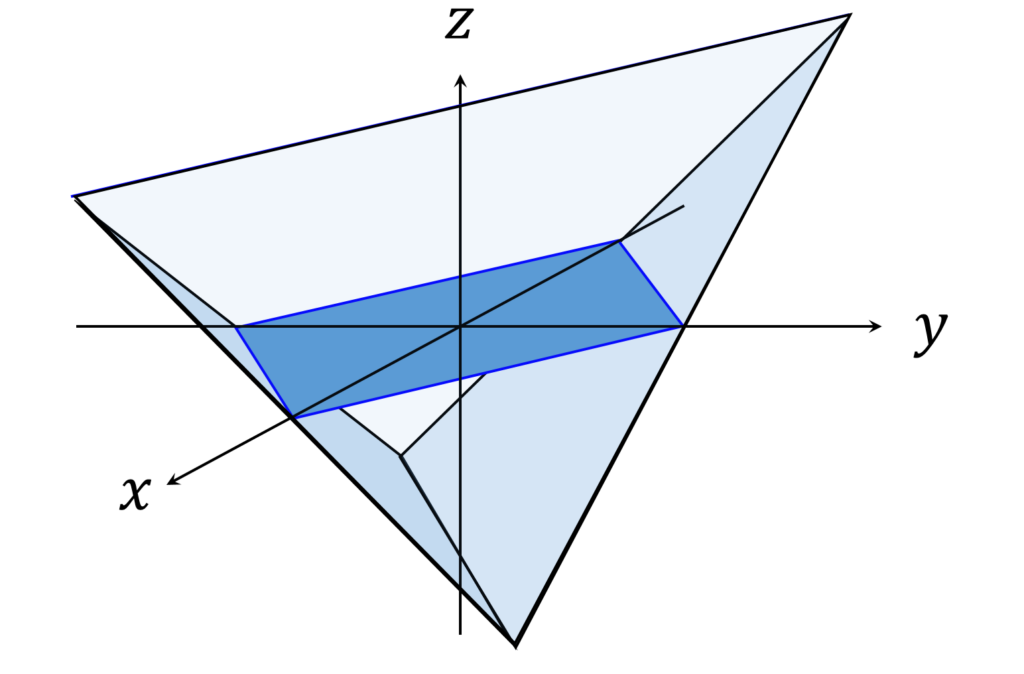
まず、 xy 平面 (z=0 ) 上の格子点を考えます(図3)。
これを +z 方向から(要は真上から)見た図が図4です。
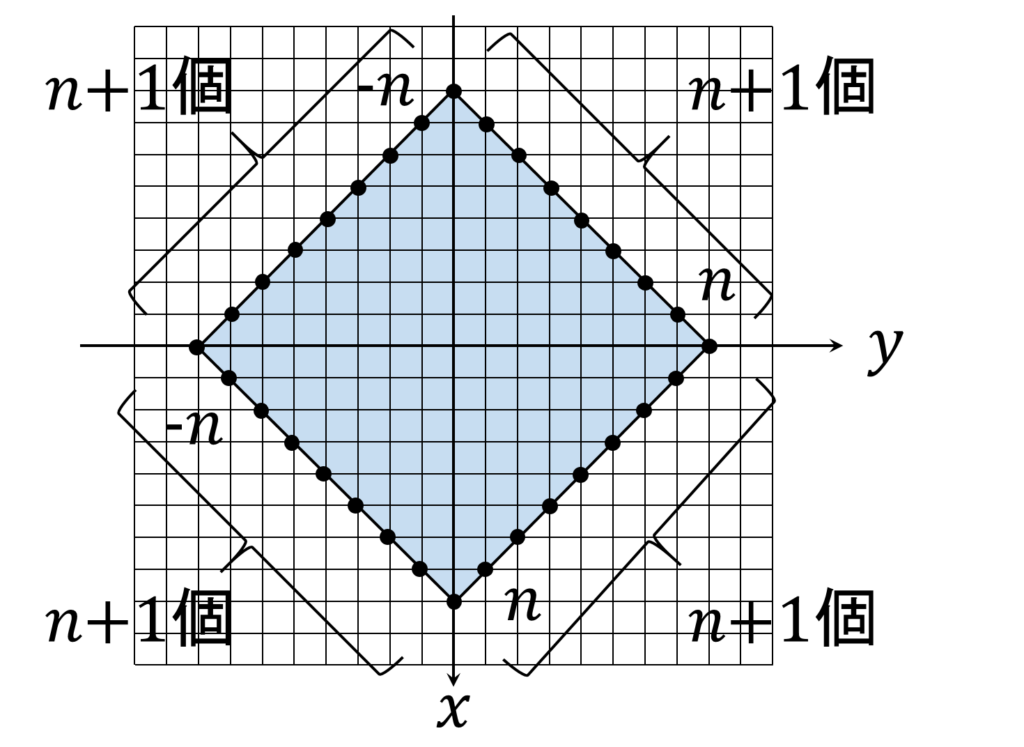
図形を平面 z=0 で切断した断面は正方形で、1辺当たりの格子点の数は n+1 個です。4辺あるのでその合計は 4(n+1) 、頂点が重複カウントされているのでこれを差し引くと、周上の格子点の合計は
4n
です。
③ xy 平面に平行な平面上の格子点
次に、 xy 平面に平行な平面 z=k(k=1,2, \cdots , n-1) 上の格子点を考えます(図5)。
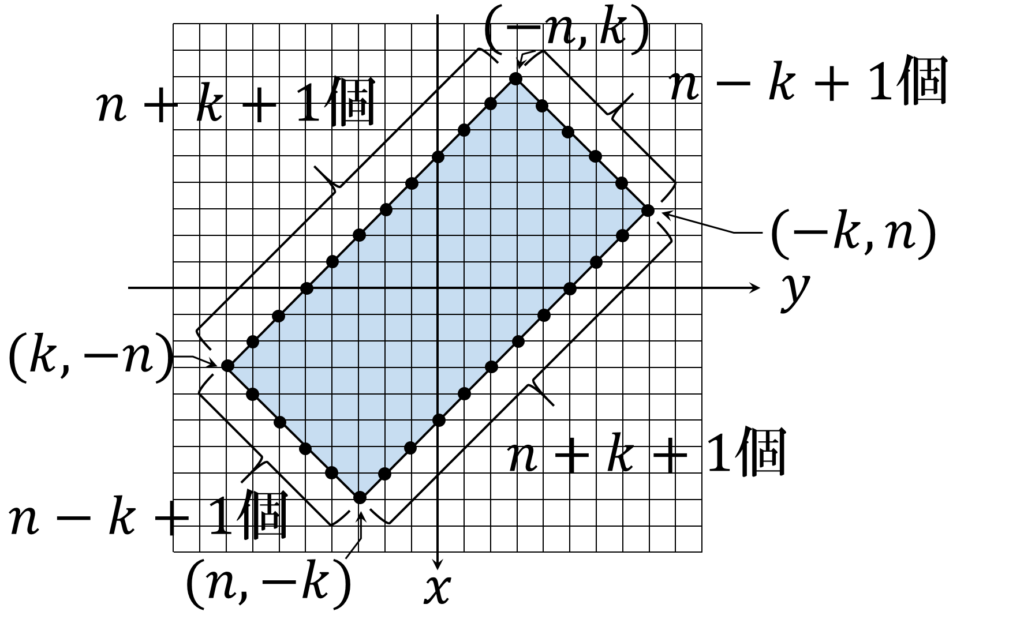
図形を平面 z=k で切断した断面の形状は矩形で、頂点の xy 座標はそれぞれ (n,-k), (-k,n), (-n,k),(k, -n) です。ここから各辺上の格子点の数を求めることが出来て、長辺上の格子点数は n+k+1 、短辺上の格子点数は n-k+1 です。
これらを合計し、頂点の重複カウントを差し引くと、頂点の数はやはり
4n
です。
更に、 xy 平面に平行な平面 z=n 上の格子点を考えます(図6)。
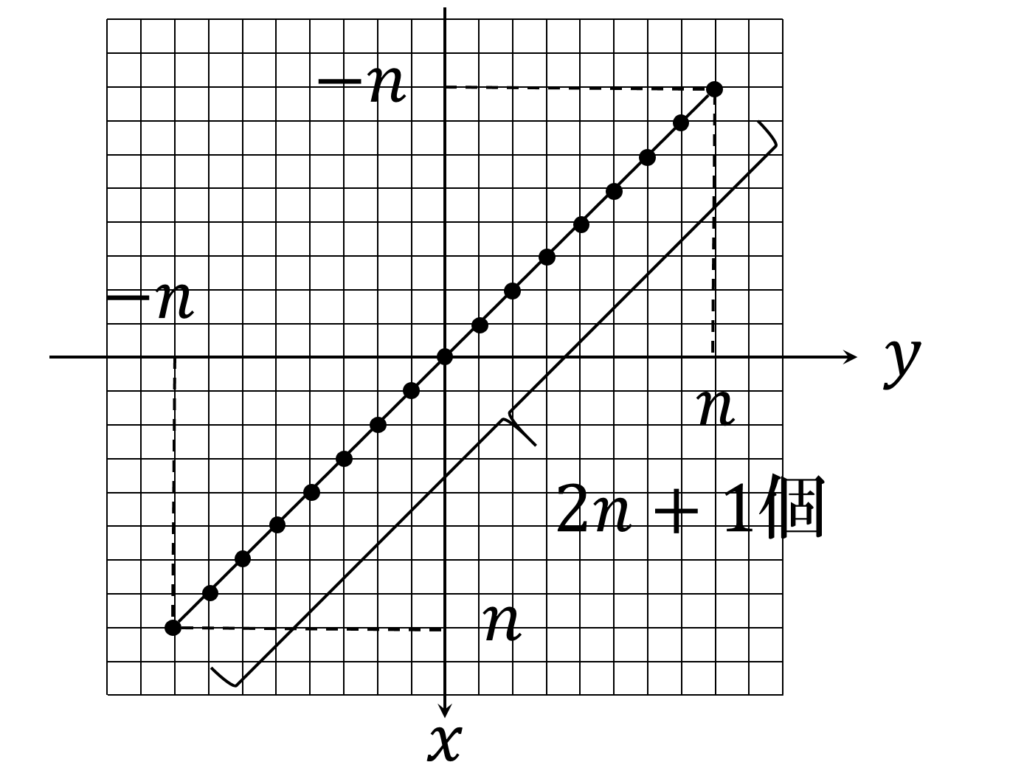
このケースでは、断面図は線分になります。格子点の数は
2n+1
です。
④集計する
xy 平面の上下で格子点の数は等しいので、四面体の表面の格子点の数は
\begin{aligned}
& 4n + 2 \times \{ 4n \times(n-1) + 2n+1 \} \\
&= 8n^2 + O(n)
\end{aligned}です。ここに O(n) は n の1次以下の項です。
こんな表記をするのは、最終的な目的が f(n) を n^3 で割って n \rightarrow \infty の極限値を求めることなので、 n の1次以下の項はどうでもいいからです。
もし1次以下の項の計算が間違っていて減点されたりしたらつまらないので、不必要な情報はあえて隠すようにしましょう。
以上の計算により、
\begin{aligned}
f(n) -f(n-1) = 8n^2 +O(n) \\
(n \geqq 2) \\
\cdots(5)
\end{aligned}を得ます。
極限 \lim\limits_{n \rightarrow \infty} \frac{f(n)}{n^3} を求める
式(5) より、
f(n) -f(1) = 8 \sum_{k=2}^n k^2 + \sum_{k=2}^n O(k)が成り立ちますが、これより
\begin{aligned}
& f(n) = 8 \sum_{k=2}^n k^2 + \sum_{k=2}^n O(k) + f(1) \\
& = 8 \sum_{k=1}^n k^2 -8+ \sum_{k=2}^n O(k) + f(1) \\
& = 8 \times \frac{n(n+1)(2n+1)}{6} \\
& \text{ } -8+ \sum_{k=2}^n O(k) + f(1) \\
& = \frac{8}{3}n^3 + O(n^2)
\end{aligned}を得ます。ここに O(n^2) は n の2次以下の項の和です。
したがって
\frac{f(n)}{n^3} = \frac{8}{3} + \frac{O(n^2)}{n^3}が成り立ちますが、明らかに
\lim_{n \rightarrow \infty} \frac{O(n^2)}{n^3} = 0なので、
\lim_{n \rightarrow \infty} \frac{f(n)}{n^3} = \frac{8}{3}を得ます。
解法のポイント
何といっても、図形のイメージをつかむことが重要です。イメージがつかめれば、格子点の数え方についての方針も立てやすくなります。
4平面を一気に描くことは難しいので、本稿で示したように2平面ずつ描いてみて、位置関係を把握するのが良いと思います。
図形が正四面体であることがわかっていれば、ずいぶん楽です。本稿で示したような簡単なやり方でも、ある程度の推測はできるので、試してみてください。
図形がイメージできれば、図形を xy 平面に平行な平面でスライスして、各面ごとに格子点をカウントしてみようという発想は、自然に浮かんでくると思います。図5の描画がちょっと難しいですが、 z=1 平面の図を描いてみれば、方向性が明らかになると思います。
格子点のカウントがまた面倒くさいので、その様な時には本稿で示したように、隣接項差分式の適用を検討してみてください。結構楽に計算できます。
