1993年東大 数学 第1問 はあの等面四面体に関する問題です。等面四面体に関する問題は京大でも出題されていましたが、本問の出題年のほうがより過去です。
問題文は以下の通りです。
すべての面が合同な四面体 ABCD がある。頂点 A,B,C はそれぞれ x,y,z 軸上の正の部分にあり、辺の長さは
\mathrm{AB} =2l-1,\mathrm{BC} =2l,\mathrm{CA} =2l+1 (l > 2)
である。
四面体 ABCD の体積を V(l) とするとき、次の極限値を求めよ。
\lim\limits_{l \rightarrow 2} \displaystyle\frac{V(l)}{\sqrt{l-2}}
本問もまた、等面四面体は直方体に内接する、というのを知っていると容易に解けますが、知らないと苦戦します。
この等面四面体の性質はもしかしたら、本問が嚆矢となって人口に膾炙するようになったのかとも思いましたが、本問の問題文には等面四面体の存在について、何の疑いも躊躇も感じられないので、当時は案外、誰でも知っている常識だったのかもしれません(知らなかったのは筆者だけなのか?)。
それでは早速、解法を見ていきます。
1993年東大 数学 第1問 解法その1(等面四面体が直方体に内接することを利用する)
四面体 ABCD が内接する直方体を、実際に構築することによって解きます。外接直方体の各辺の長さが明らかになれば、四面体 ABCD の体積は容易に求められます。その際、座標軸とか全然使いません。やり方は1999年京大第4問と同じです。
四面体 ABCD に外接する直方体が存在するならば、その各面の対角線が四面体の辺に対応します。そこで、そうなるように直方体の各辺の長さを決めます。
すなわち、以下の連立方程式を考えます。
\left \{
\begin{aligned}
x^2+y^2 &= (2l-1)^2 \\
y^2+z^2 & = 4l^2 \\
x^2+z^2 & = (2l+1)^2
\end{aligned}
\right.この連立方程式は正の実数解
\begin{aligned}
& x = \sqrt{2l^2+1} \\
& y = \sqrt{2l^2 -4l } \\
& z = \sqrt{2l^2 +4l } \
\end{aligned}をもつので、それらを順に a,b,c と置きます。
このとき、各辺の長さがそれぞれ a,b,c である直方体において、
\begin{aligned}
\mathrm{AB} &=2l-1 \\
\mathrm{BC} &=2l\\
\mathrm{CA} &=2l+1
\end{aligned}
および、
\begin{aligned}
\mathrm{DA} &=2l\\
\mathrm{DB} &=2l+1 \\
\mathrm{DC} &=2l-1 \\
\end{aligned}
が成り立ちます(図1)。
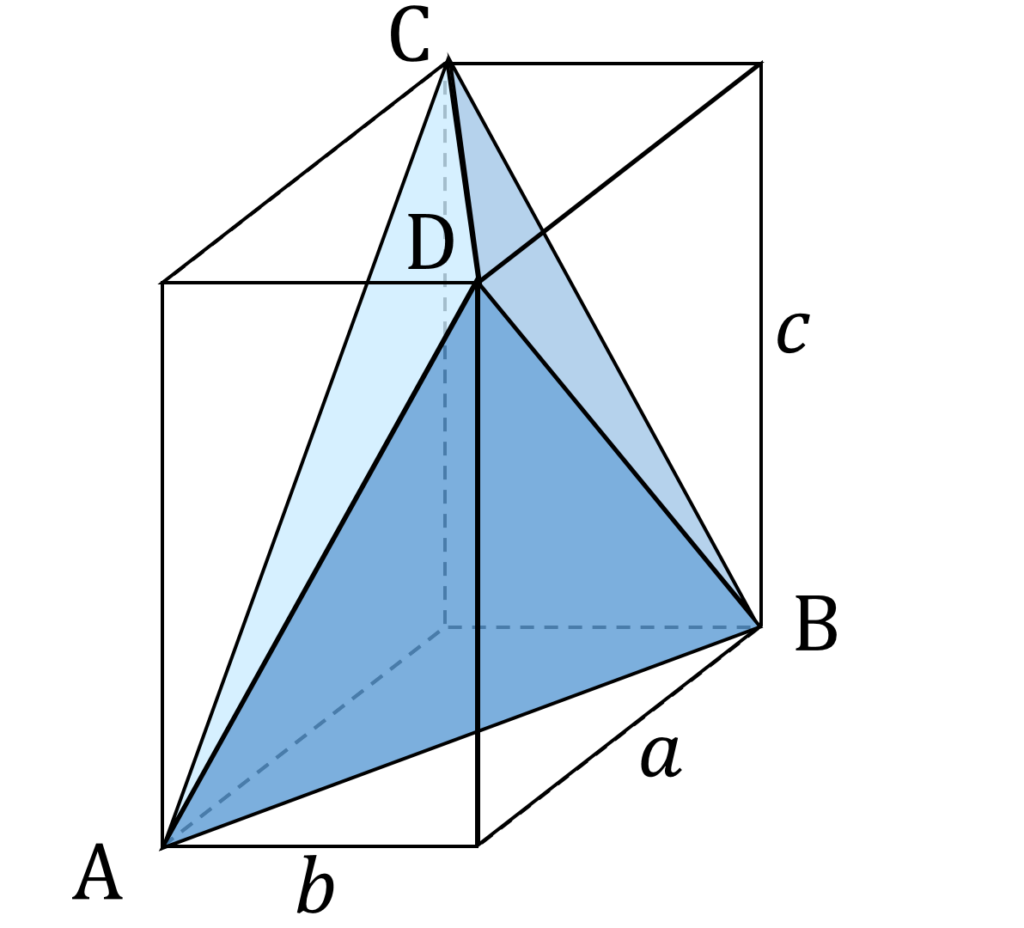
したがって、四面体 ABCD は設問の等面四面体と合同であり、それは各辺の長さがそれぞれ a,b,c の直方体に内接します。
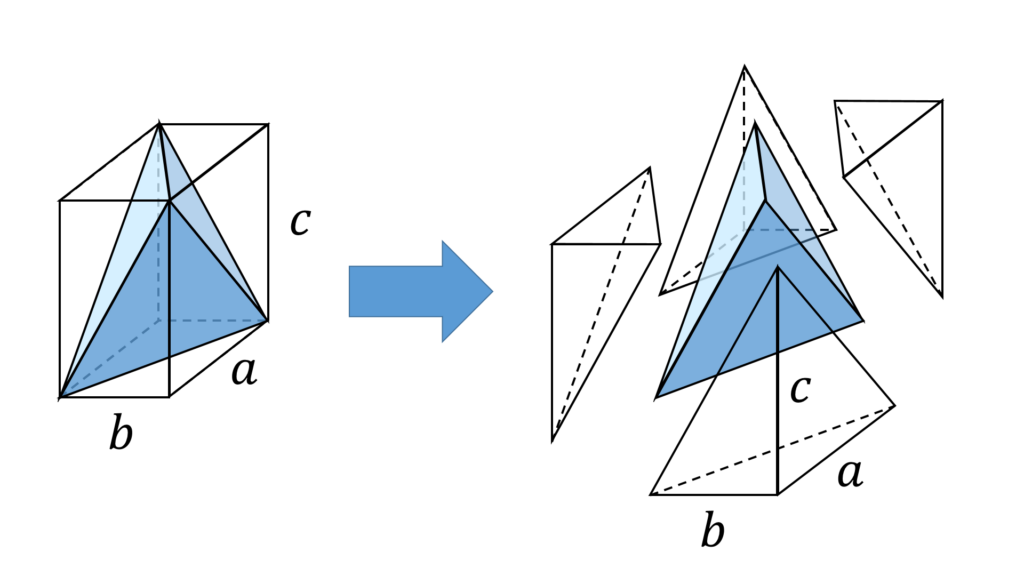
次に四面体 ABCD の体積 V(l) を求めますが、図2から明らかなように、
\begin{aligned}
&V(l) \\
= & abc - 4 \times \frac{abc}{6} \\
= & \frac{abc}{3} \\
= &\frac{2l\sqrt{(2l^2+1)(l-2)(l+2)}}{3}
\end{aligned}です。
ゆえに、
\begin{aligned}
& \lim_{l \rightarrow 2 } \frac{V(l)}{\sqrt{l-2 } } \\
=& \lim_{l \rightarrow 2 }\frac{2l\sqrt{(2l^2+1)(l-2)(l+2)}}{3\sqrt{l-2 }} \\
=& \lim_{l \rightarrow 2 }\frac{2l\sqrt{(2l^2+1)(l+2)}}{3} \\
= & 8
\end{aligned}が成り立ちます。
1993年東大 数学 第1問 解法その2(頂点Dの座標を求める)
等面四面体が直方体に内接することを知らない場合、頂点Dの座標を求めて、そこから四面体の体積 V(l) を求めます。
頂点 A,B,C がそれぞれ x,y,z 軸上の正の部分にあるので、それぞれの座標を
\begin{aligned}
\mathrm{A}(a,0,0) \\
\mathrm{B}(0,b,0) \\
\mathrm{C}(0,0,c)
\end{aligned}と置きます。ここで a,b,c > 0 です。
このとき、勘のいい人なら、「D の座標を (a,b,c) と置いたら、ひょっとしてうまくいくのでは」と思いつくかもしれませんが、ビンゴです。
\begin{aligned}
& a = \sqrt{2l^2+1} \\
& b = \sqrt{2l^2 -4l } \\
& c = \sqrt{2l^2 +4l } \
\end{aligned}なので、 D から平面 ABC への垂線の長さを求めることが出来て、 V(l) を算出できます。
しかしこのやり方は計算が大変です。そこで図1を描いて、四面体 ABCD は3辺の長さがぞれぞれ a,b,c の直方体に内接することに気が付く必要があります。
D の座標が具体的にわかっているので、図1を描くのは容易だと思います。図が描ければ、直方体に内接することはすぐにわかると思います。
四面体が直方体に内接することに気が付けば、あとは解法その1と同様の手順で V(l) および極限値を求めることが出来ます。
D の座標をニュータイプ的にひらめけなかった場合は、方程式を立てて座標を求めます。
四面体 ABCD が等面四面体になるとき、
DA = BC
DB = AC
DC = AB
です(そうでないと、等面四面体にならない)。そこで D の座標を (x,y,z) と置きます。すると x,y,z は連立方程式
\left \{
\begin{aligned}
(x-a)^2+y^2+z^2 = \mathrm{BC}^2 \\
x^2+(y-b)^2+z^2 = \mathrm{AC}^2 \\
x^2+y^2+(z-c)^2 = \mathrm{AB}^2
\end{aligned}
\right .の解です。
ところが、
\begin{aligned}
& \mathrm{BC}^2 = b^2 + c^2 \\
& \mathrm{AC}^2 = a^2 + c^2 \\
& \mathrm{AB}^2 = a^2 + b^2
\end{aligned}なので、
\left \{
\begin{aligned}
(x-a)^2+y^2+z^2 = b^2 +c^2 \cdots(1)\\
x^2+(y-b)^2+z^2 = a^2 + c^2 \cdots(2)\\
x^2+y^2+(z-c)^2 = a^2 + b^2 \cdots(3)
\end{aligned}
\right .です。
式をにらんでいるうちに、 (x,y,z) =(a,b,c) が解の1つであることに何となく気が付くことが出来れば、 D の座標を (a,b,c) と置いて何の問題もないので、あとは外接直方体の秘跡に気づいて、解法その1と同じ手順で答えを得ます。
もう少しきっちりと解きたい場合は、連立方程式を実際に解きます。
式(1)から式(2)を引いて、
-ax+by = b^2- a^2 \cdots (4)
式(1)から式(3)を引いて
-ax+cz = c^2 -a^2 \cdots(5)
式(4)、式(5)を式(1)に代入して、
\begin{aligned}
& (x-a)^2 \\
&+\left (b+\frac{ax-a^2}{b} \right )^2 \\
&+ \left( c+\frac{ax-a^2}{c} \right )^2 \\
&= b^2+c^2 \\
\end{aligned}
を得ます。これを解くと
x=a, x = a-a \frac{4b^2c^2}{a^2b^2 + a^2c^2+b^2c^2}です。よって連立方程式の答えは
x =a \\ y=b \\ z =c
または
x = a- a\frac{4b^2c^2}{a^2b^2 + a^2c^2+b^2c^2} \\
y = b- b\frac{4a^2c^2}{a^2b^2 + a^2c^2+b^2c^2} \\
z = c-c\frac{4a^2b^2}{a^2b^2 + a^2c^2+b^2c^2} \\どちらの値を使っても同じ答えが出ますが、簡単な方がいいので D の座標を (a,b,c) とおき、あとは解法その1の手順で答えを得ます。
解法のポイント

等面四面体の問題は、やはり直方体に内接することを知っていると、断然有利です。特に本問のように体積を求める場合は、計算の楽さ加減が全然違います。このことは脳裏にきっちり刻み付けておきましょう。
