存在領域の難問 – 1988年東大 数学 第3問

1988年東大 数学 第3問 は、条件を満たす点の存在領域を求める問題です。問題文は以下の通りです。
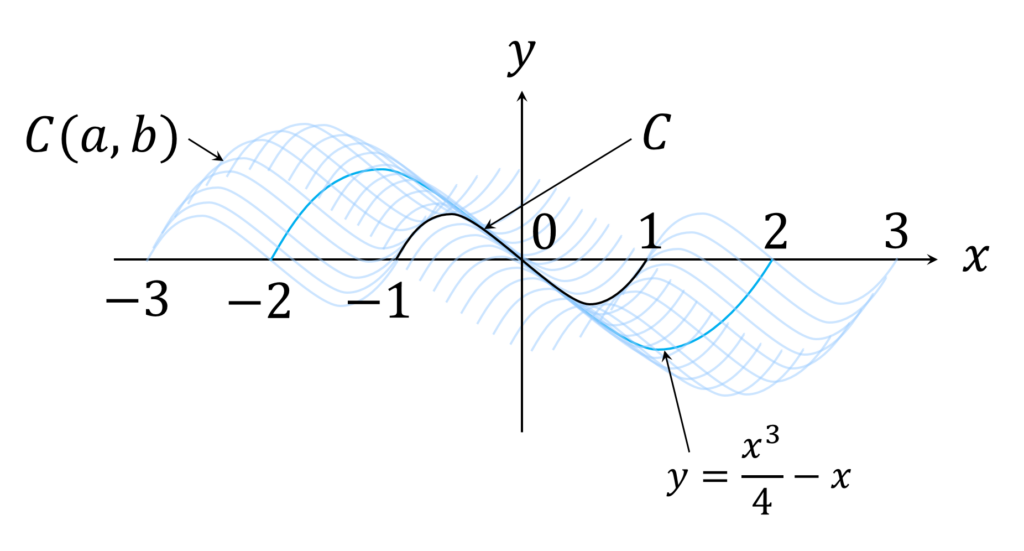
C を y=x^3−x, \text{ } −1≦x≦1 で与えられる xy 平面上の図形とする. 次の条件をみたす xy 平面上の点 P 全体の集合を図示せよ.
条件:「 C を平行移動した図形で, 点 P を通り, かつもとの図形 C との共有点がただ1点であるようなものが,ちょうど3個存在する.」
いかがでしょうか。問題文が複雑すぎて、全然頭に入ってきません。とりあえず後回しにしたい問題ですが、順を追って解きほぐしていきましょう。
1988年東大 数学 第3問の解法 – Step1: 平行移動のイメージをつかむ
本問の凶悪なところは、元の図形の平行移動と、平行移動した3図形が1点で交わると言う2段構えになっていることで、特に後のほうが訳が分かりませんが、まずは前半の、「共有点が1点のみの平行移動」がどういうことを意味しているのか、明らかにしていきます。
関数と記号の定義
x \in \mathbb{R} の関数 f(x) を、
f(x) = x^3 - x
と定義し、元の図形 C を x 軸方向に a 、 y 軸方向に b 平行移動した図形を C(a,b) と定義します。すなわち、
\begin{aligned}
C(a,b) = \{(x,y) \in \mathbb{R^2} | y = f(x-a) +b, \\
-1 +a\leqq x \leqq 1+a\}
\end{aligned}です。当然、
\begin{aligned}
C(0,0) = C =\{(x,y) \in \mathbb{R^2} | y = f(x) , \\
-1 \leqq x \leqq 1\}
\end{aligned}です。
C と C(a,b) の交点について考察するので、 x \in \mathbb{R} の関数 F(x) を
\begin{aligned}
F(x) &= f(x) -f(x-a) -b \\
& = 3ax^2 -3a^2 x +a^3 -b \\
& = 3a \left ( x- \frac{a}{2} \right ) ^2 + \frac{3}{4}a^3 -b
\end{aligned}と定義します。
a > 0 の場合の考察
a > 0 のとき、 C と C(a,b) の x の変域の共通範囲は -1+a \leqq x \leqq 1 なので、交点があるとすればその範囲内です。必然的に、 a \leqq 2 であることが必要です。
C と C(a,b) の交点が1つであるということは、方程式 F(x) = 0 が -1+a \leqq x \leqq 1 の範囲で解を1つだけ持つということです。
ところが、
F(1) = F(-1+a) = (a-1)^3 - b +1
です。放物線 y = F(x) は区間 [-1+a, 1] の両端で同じ値を取るので、その軸 x = \frac{a}{2} は区間の中点であり、かつ、そこで最小値を取ることがわかります。
したがって、方程式 F(x) = 0 がその範囲内に解を1つだけ持つための必要十分条件は、 F(\frac{a}{2}) = 0 です。
\begin{aligned}
F(\frac{a}{2}) &= f(\frac{a}{2}) -f(\frac{a}{2} -a) -b \\
& = 2f(\frac{a}{2}) -b \\
& = \frac{a^3}{4} -a -b
\end{aligned}なので、方程式 F(x) = 0 が -1+a \leqq x \leqq 1 の範囲で解を1つだけ持つための必要十分条件は、 a \leqq 2 かつ
b = \frac{a^3}{4} -aであることです。このとき、方程式 F(x) = 0 は重根を持つので、 C と C(a,b) は1点で接します。
a < 0 の場合の考察
a <0 の場合も同様です。 C と C(a,b) の交点が1つであるということは、方程式 F(x) = 0 が -1 \leqq x \leqq 1+a の範囲で解を1つだけ持つということです。必然的に、 a \geqq -2 であることが必要です。
あとは a> 0 のときと同じロジックにより、方程式 F(x) = 0 が -1 \leqq x \leqq 1+a の範囲で解を1つだけ持つための必要十分条件は、 a \geqq -2 でかつ、 b = \frac{a^3}{4} -a であることがわかります。
a = 0 の場合の考察
最後に a = 0 の場合ですが、 b = 0 ならば平行移動していないので除外、 b \ne 0 の場合は C と C(a,b) は交点を持たないのでやはり除外です。
C と C(a,b) が交点を1つだけ持つための必要十分条件
ゆえに、 C と C(a,b) が交点を1つだけ持つための必要十分条件は、
-2 \leqq a \leqq 2 \\
\text{かつ} \\
a \ne 0 \\
\text{かつ} \\
b = \frac{a^3}{4} -aです。
平行移動の範囲はある領域になると思っていましたが、意外なことに特定の曲線にそって元の図形と接するように移動させたときのみ、 C と C(a,b) の交点は1つになることがわかりました。
C(a,b) の動く範囲のイメージは、図1の通りです。