存在領域の難問 – 1988年東大数学第3問

2021年12月13日2023年2月28日

　ここで $a$ の関数 $g_{s,t}(a)$ を

g_{s,t}(a) =\frac{3}{4}a^3 -3sa^2+3s^2a +s-s^3 +t

と定義します。

　このとき、 $a = 0$ は $g_{s,t}(a) = 0$ の解ではないので、 $g_{s,t}(0) \ne 0$ 、すなわち

t \ne s^3 -s

です。

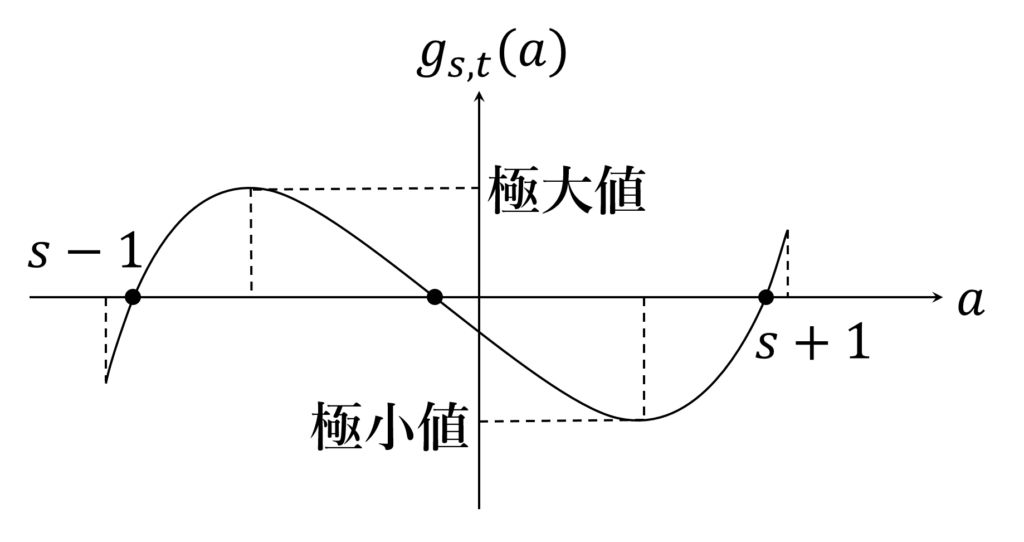
　よって、方程式 $g_{s,t}(a)=0$ が $s-1 \leqq a \leqq s+1$ の範囲に0以外の3つの異なる実数解を持つための必要十分条件は、

$t \ne s^3 -s$
かつ
$s-1 < a < s+1$ の範囲内に極大値、極小値を取る
かつ
$g_{s,t}(s-1) \leqq 0$
かつ
$g_{s,t}(s+1) \geqq 0$
かつ
極大値>0
かつ
極小値<0

　です（図2）。

　 $g_{s,t}(a)$ を $a$ で微分すると、

\begin{aligned} \frac{d}{da}g_{s,t}(a) &=\frac{9}{4}a^2 -6s+3s^2 \\ & =\frac{3}{4}(3a-2s)(a-2s) \end{aligned}

なので、関数 $g_{s,t}(a)$ は $s \ne 0$ のとき $a = \frac{2}{3}s$ および $a = 2s$ のときに極値を取ります。

　 $s = 0$ のとき、 $g_{0,t}(a)$ は単調増加関数になり、 $g_{0,t}(a) = 0$ は高々1個しか実数解を持ちません。よって、 $s = 0$ は除外します。

　 $g_{s,t}(a)$ は $s-1 < a < s+1$ の範囲内に極大値、極小値を取るので、これを具体的な不等式に表現すると、

s-1 < \frac{2}{3}s,2s < s+1

です。よって、 $s$ の範囲は、

-1 < s < 1

ですが、 $s=0$ を除外するので

-1 < s < 0, \text{または} 0< s<1

となります。

　極値の値は $g_{s,t}(\frac{2}{3}s),g_{s,t}(2s)$ ですが、ここで気をつけなければならないのは、 $s$ の正負によって、それらのどちらが極大値になり、どちらが極小値になるかが入れ替わることです。

　 $s > 0$ のとき、 $\frac{2}{3}s < 2s$ なので、 $g_{s,t}(\frac{2}{3}s)$ が極大値、 $g_{s,t}(2s)$ が極小値です。

　 $s < 0$ のとき、 $2s < \frac{2}{3}s$ なので、 $g_{s,t}(2s)$ が極大値、 $g_{s,t}(\frac{2}{3}s)$ が極小値です。

　以上をまとめると、方程式 $g_{s,t}(a)=0$ が $s-1 \leqq a \leqq s+1$ の範囲に0以外の3つの異なる実数解を持つための必要十分条件は、 $(s,t)$ が以下の連立不等式を満たすことです。

\left \{ \begin{aligned} -1 < s < 0, & \text{または} 0 < s < 1 & \cdots(1) \\ t & \ne s^3-s &\cdots(2)\\ g_{s,t}(s-1) & \leqq 0 &\cdots(3)\\ g_{s,t}(s+1) & \geqq 0 & \cdots(4)\\ g_{s,t}(\frac{2}{3}s) &> 0(s>0) &\cdots(5)\\ g_{s,t}(\frac{2}{3}s) &< 0(s<0) &\cdots(5) \\ g_{s,t}(2s) &< 0(s>0)& \cdots(6) \\ g_{s,t}(2s) &> 0(s<0) &\cdots(6) \\ \end{aligned} \right .

P = (s,t)

s,t