存在領域の難問 – 1988年東大 数学 第3問
点Pの存在領域を図示する
以上を図示すると、図3の通りです。
図3において、実線境界は対象範囲に含みます。破線境界は対象範囲に含みません。
また、 (1,0),(-1,0),(\frac{3}{5},-\frac{72}{125}),(-\frac{3}{5},\frac{72}{125}),(0,0) の各点は対象範囲に含みません。
解領域の幾何学的意味合い
y = \frac{1}{4}(x-1)(x+1)(x-3) は、図形 C を題意に沿って平行移動したときの、右端の軌跡です。また y = \frac{1}{4}(x-1)(x+1)(x+3) は、左端の軌跡です。
一方、 y =x^3-x および y = \frac{1}{9} x^3 -x は、平行移動図形 C(a,b) が共通に接する曲線です（図4）。
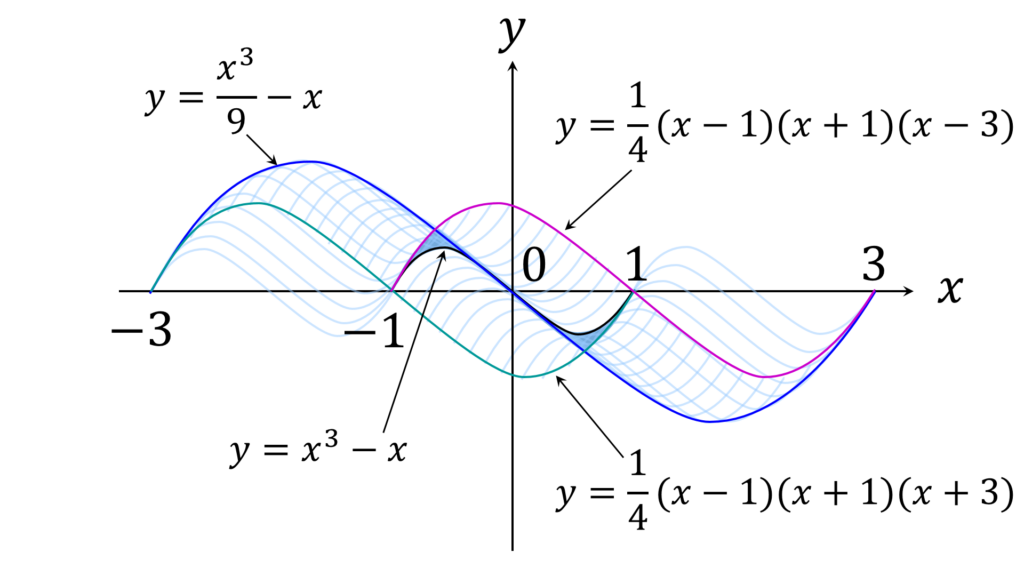
出来上った全体像はシンメトリカルで、思いのほか美しいものになっています。
解法のポイント
本問は条件を満たす点の移動領域を図示する問題で、数学的には点の座標が満たす不等式を求めることがゴールになります。
順を追って段取りを踏んでいけば、解けない問題ではありませんが、その段取りを踏むことが、至難の業です。
設問の条件を、「平行移動した図形のうち、元の図形との共有点が1つのもの」のうち「3図形が1点で交わる」点の存在領域を求める、というように、2段階に分解することが第一歩です。問題文の日本語がこなれていないので、題意を正しく把握するのが大変です。
交点の数の問題は、2次方程式または3次方程式の解の個数の問題に帰着できるので、それ自体は容易に解けることと思います。ただ、本問では変域の範囲に、特に注意が必要です。
移動する図形が関数の一部で有限の変域を持つので、移動元と移動先の図形が交点を持つには、それぞれの変域が交わっていることが必要です。
さらに、3つの図形が1点で交わるためには、3つの変域が交わるという、さらに複雑な条件を考える必要が出てきます。これらに気が付かないと、正解にたどり着けないので気をつけましょう。
極大値、極小値が条件によって入れ替わる、というのも、何気にいやらしい感じです。条件分岐がより複雑になってしまいます。
全般に気を付けるべきことが多いので、制限時間内に回答するのは難しい問題です。問題文が訳分からんちんなこともあるので、本問は捨て問確定でしょう。
ただ、本問は論理的思考力を養うには、良い教材です。問題の定式化や回答の段取りをどうやれば短い時間内に思いつくことができるか、いろいろと検討してみると実力アップにつながると思います。