2001年東大 数学 第5問 は、一見してどの分野の問題かわかりません。問題文も長く、捨て問オーラ全開です。問題文は以下の通りです。
容量 1 リットルの m 個のビーカー(ガラス容器)に水が入っている。m ≧ 4 で空のビーカーは無い。入っている水の総量は 1 リットルである。また x リットルの水が入っているビーカーがただ一つあり,その他のビーカーには x リットル未満の水しか入っていない。
このとき,水の入っているビーカーが 2 個になるまで,次の (a) から (c) までの操作を,順に繰り返し行う。
(a) 入っている水の量が最も少ないビーカーを一つ選ぶ。
(b) さらに,残りのビーカーの中から,入っている水の量が最も少ないものを一つ選ぶ。
(c) 次に,(a) で選んだビーカーの水を (b) で選んだビーカーにすべて移し,空になったビーカーを取り除く。
この操作の過程で,入っている水の量が最も少ないビーカーの選び方が一通りに決まらないときは,そのうちのいずれも選ばれる可能性があるものとする。
(1) x < \frac{1}{3} のとき,最初に x リットルの水の入っていたビーカーは,操作の途中で空になって取り除かれるか,または 最後まで残って水の量が増えていることを証明せよ。
(2) x > \frac{2}{5} のとき,最初に x リットルの水の入っていたビーカーは,最後まで x リットルの水が入ったままで残ることを証明せよ。
本問には、微積分や三角関数のような、高校で習う数学の単元がほとんど出てきません。その点では世紀の難問1998年後期第3問に似ていますが、あちらでは剰余類が出てきた(解法によっては行列や数学的帰納法を使う場合もある)のにもかかわらず、本問ではそれすら出てきません。
本問で唯一出てくるのは、背理法です。これを武器に、論理的思考力でもって一気に調伏します。パズル好きの人向けの問題と言えるでしょう。
それでは早速、見ていきます。
2001年東大 数学 第5問 題意の整理
問題文に描かれたオペレーションは、以下の通りです。
- 各ビーカーを水量の昇順に並べ、1番から順に番号を振る。同水量のビーカーが複数あった場合の並べ方は、任意
- 1番のビーカーの水を、2番のビーカーに入れる
- 空になった1番のビーカーは除ける
- 1~3の手順を、残りビーカーが2つになるまで繰り返す
水量の少ないビーカーから、じわじわと集約を掛けていくイメージです(図1)。
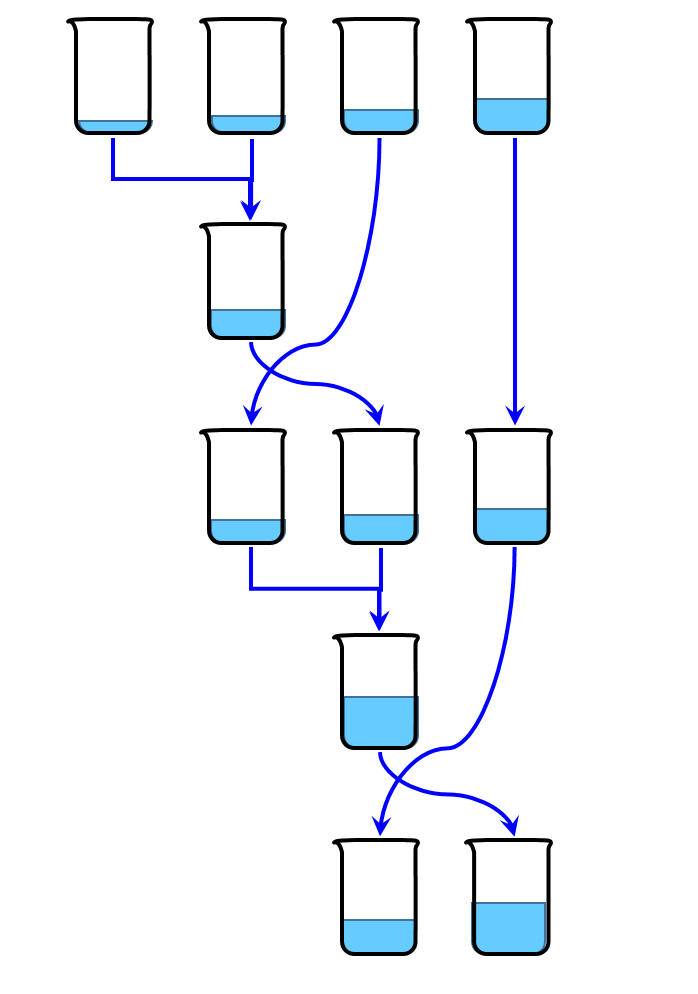
2001年東大 数学 第5問 小問1の解法
題意が把握できたところで、小問1に取り掛かります。小問1は思いのほか簡単です。背理法を使って証明します。
最初に x リットルの水が入っていたビーカーおよびその水量を、 b_0 と表記します。初期状態では b_0 = x です。
x < \frac{1}{3} のとき,最後まで b_0 = x であったと仮定します。
すると、最終状況において b_0 は最大か、2番目に多いかのどちらかですが、 b_0 = x < \frac{1}{3} なので、 b_0 が最大と言うことはあり得ません。
したがって、2番目に水が多いということになります。
ここで、最後から1つ前の、ビーカーが3つある状況を考察します。 b_0 の他のビーカーおよびその水量を b_1, b_2 と置き、 b_1 \leqq b_2 であるとします。
このとき、 b_0 は最後まで変化しないのですから、ビーカーの水量に
b_1 \leqq b_2 \leqq b_0 = x < \frac{1}{3}の関係が成り立っているはずです。ところがこれは、 b_1 + b_2 + b_0 = 1 であることに矛盾します。
ゆえに、 b_0 の水量が最後まで変化しないということはあり得ない、すなわち b_0 = 0 か、または b_0 > x のいずれかであることが証明できました。
