伝説の超難問の解法まとめ – 1998年東大数学後期第3問

2022年4月1日2024年3月11日

　史上最強の超難問として今なお君臨し続ける、1998年東大数学後期第3問。ネット上にはいろいろな解法がUPされており、本ブログでも過去に取り上げていますが、本稿ではそれらを紹介していきます。そして、各解法が本質的に２パターンに収斂することを示します。

1998年東大数学後期第3問とは

　そもそも1998年東大数学後期第3問とはどんな問題なのか、ですが、問題文が相当長いので、引用は断念します。ググると問題文の画像がヒットしますので、そちらをご覧ください。

　問題の要旨ですが、側面に竹ひごをぷすぷす刺せる、オセロの駒をイメージしてください。このオセロの駒に、竹ひごで別のオセロの駒をつなぎます。１つのオセロに、何本でも竹ひごを刺せるものとします。

　オセロの追加方法には、以下の2種類があります。

　オセロ列の一番端に、新しく白オセロを追加します。追加された側のオセロは、色を反転させます。

　オセロとオセロの間に、新しい白オセロを挿入します。もともとあった、両隣のオセロは色を反転させます。

　要は、新規追加のオセロは白、追加されたオセロに隣接するオセロは色を反転させる、というルールです。

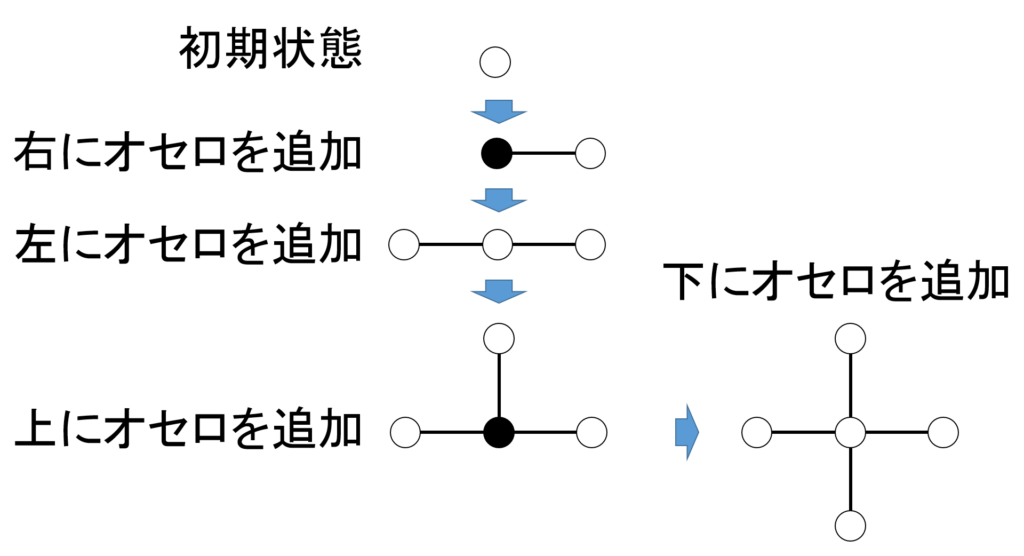
　初期状態は、白のオセロの駒が１つだけです。これに上記の要領で、竹ひごとオセロをどんどんつないでいきます（図1参照）。

　この問題には、小問が2つあります。小問1は、以下の図2（オセロの駒が全部白）が生成できることを示せ、というものです。小問2は、図3のようにオセロを1列につないで、しかもオセロが全部白の時の、オセロの数が満たす条件は何か、というものです。

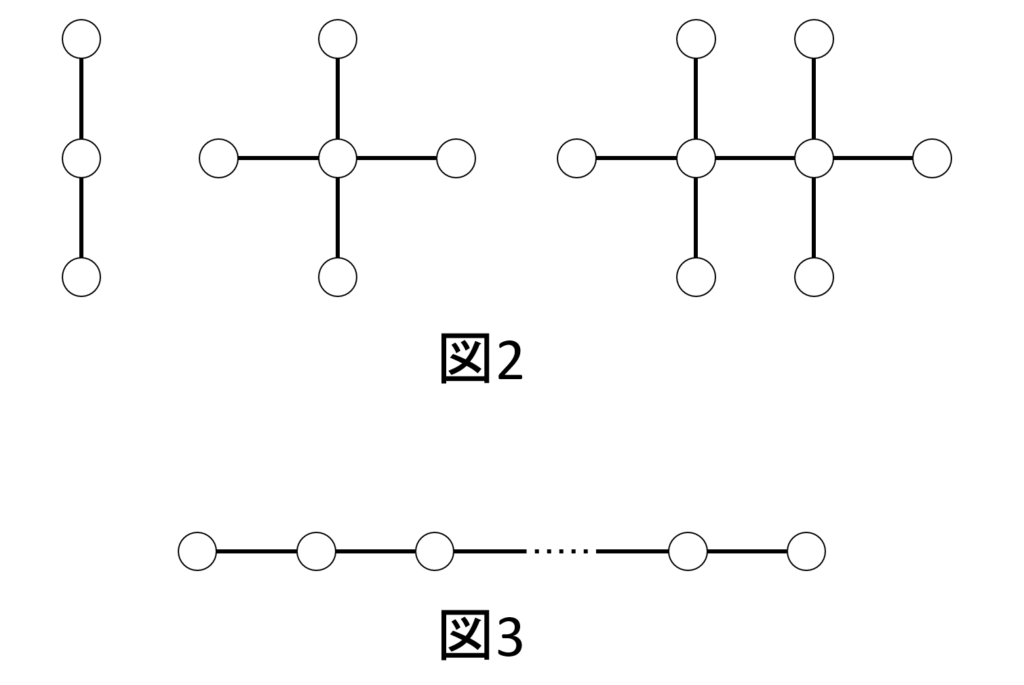
　超難問と言いながら、実は小問1は、パズル感覚でさくっと楽しく解けます。超難問なのは小問2の方です。