記号の準備
証明に当たって、以下の記号を定義しておきます。
集合の定義
\mathfrak{G} = \{ すべてのオセロ列 \}
G = \{ 1個の白オセロを起点に、操作1および操作2を施して生成されるオセロ列 \}
つまり、 \mathfrak{G} は、特に何も考えずに1列につなげたオセロ列の集合、 G は題意に沿って、1個の白オセロから生成されたオセロ列の集合です。当然、 G \subset \mathfrak{G} が成り立ちます。
剰余類の表記
また、 n \in \mathbb{Z} を3で割ったあまりを
mod_3 (n)
と表記することにします。 mod_3(3) =0, mod_3 (7) = 1, mod_3 (-1) = 2 です。
同様に、 n \in \mathbb{Z} を2で割ったあまりを
mod_2 (n)
と表記します。
拡張オセロ列
オセロ列への操作が2種類あるため、より訳が分からなくなってしまうのですが、仮にオセロ列の「端」がなくなれば、操作1が不要になって、証明が簡素化されることが期待できます。
そこで、初期状態の1個の白オセロの左右に別のオセロ石 o_L,o_R をそれぞれ付け加えて3個状態のオセロ列
o_L - \text{〇} - o_R
にし、これに操作2のみを加えてオセロ列を生成します。こうやって生成されたオセロ列を拡張オセロ列と呼び、その集合を EG と定義します。
EG = \{ o_L -〇- o_R から操作2のみを施して生成された拡張オセロ列 \}
EG も G 同様、 \mathfrak{G} の部分集合です。
o_L,o_R の色の選び方は、解法によって異なっていますが、実はどのように選んでも、同じ論法で証明することが出来ます。
EG の各要素は、両端のオセロを1個ずつ取り去ることによって、元のオセロ列集合 G と、操作も含めて1対1対応します(図5)。
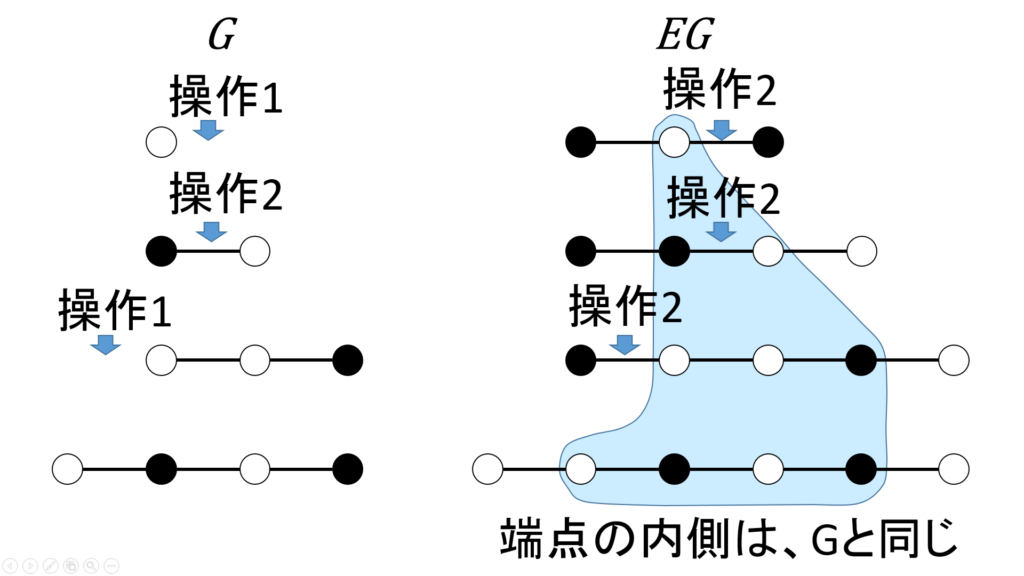
したがって、 g \in G ならば、適当なオセロ石 o_L,o_R を左右に付加したオセロ列 o_L - g - o_R は EG の要素になります。
この対偶を取ることで、以下の命題を得ます。
命題2
\bm{g \in \mathfrak{G} } の両端にオセロ石 \bm{o_L,o_R } をどのように付加しても \bm{o_L - g - o_R \notin EG } のとき、 \bm{g \notin G } である
オセロ列の構造定義
オセロ列 g \in \mathfrak{G} の構造を、図6のように定義します。
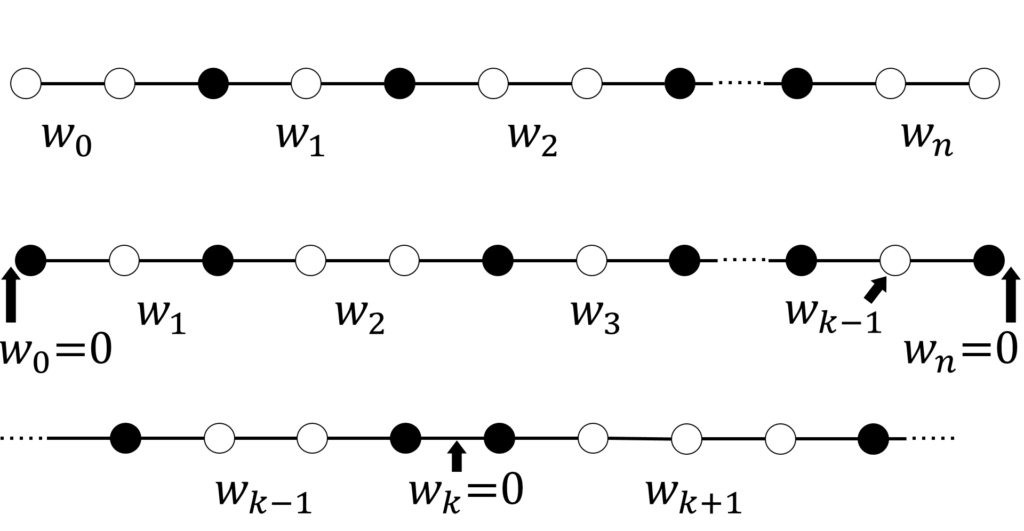
両端が白オセロであるオセロ列 g において、連続する白オセロを1つの群とし、その個数を左から順に w_k (k=0,1, \cdots ,n) と定義します。(図6上)。
g の左端が黒オセロの時は一番左に個数0の白オセロ群が存在していると解釈し、 w_0=0 とします。同様に g の右端が黒オセロの時は、一番右に個数0の白オセロ群があると解釈し、 w_n=0 とします(図6中)。
黒オセロは連続していても群にはまとめません。黒オセロと黒オセロの間に個数0の白オセロ群が存在していると解釈し、 w_k=0 とします(図6下)。
不変量関数
f を集合 \mathfrak{S} 上の関数とします。 f が \mathfrak{S} の部分集合 S の全て要素に対して特定の値を取るとき、 f をSの不変量関数と呼ぶことにします。また、その特定の値を S の不変量と呼びます。
本稿で取り上げる各解法は殆どが、G または EG の不変量関数を求め、長さ 3m +2 の白オセロ列またはその拡張が不変量を取らないことを示すことで、白オセロ列が生成されないことを証明しています。
以下、各解法を順次紹介していきます。