体積積分のブービートラップ – 2022年東大 数学 第5問
2022年東大 数学 第5問 は、図形が移動してできる軌跡の体積を求める問題です。問題分は以下のとおりです。
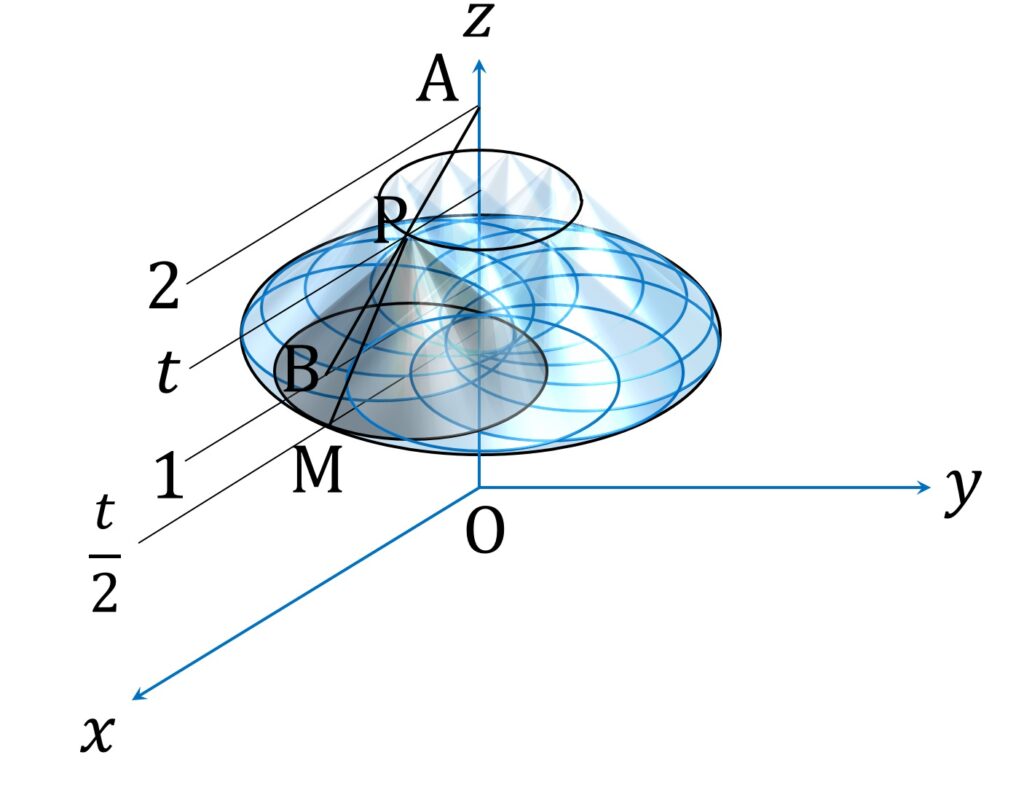
座標空間内の点 A(0,0,2) と点 B(1,0,1) を結ぶ線分 AB を z 軸のまわりに1回転させて得られる曲面を S とする。 S 上の点 P と xy 平面上の点 Q が PQ = 2 を満たしながら動くとき、線分 PQ の中点 M が通過しうる範囲を K とする。 K の体積を求めよ。
東大は時々この手の、図形の軌跡問題を出題します。過去にも2020年第2問や1988年の第3問などがありますが、いずれも一癖ある難問です。翻って本問はどうかというと、やはり設問がくどくどといやらしく、嫌な予感がします。
それでは、早速見ていきましょう。
2022年東大 数学 第5問 の解法
設問の意味を図にする
曲面 S は点 A を頂点とする円錐（の斜面）ですが、最初からこれを相手にするとわけがわからなくなるので、まずは回転させる前の線分 AB を基点に考察します。
点 P を線分 AB 上の点とし、その座標を (2-t,0,t) と置きます。ここに 1 \leqq t \leqq 2 です。このとき、点 Q は xy 平面上にあって PQ = 2 であることから、中心が ( 2-t,0,0) 、半径が \sqrt{ 4- t^2 } の、 xy 平面上の円周上に有ります（図1）。
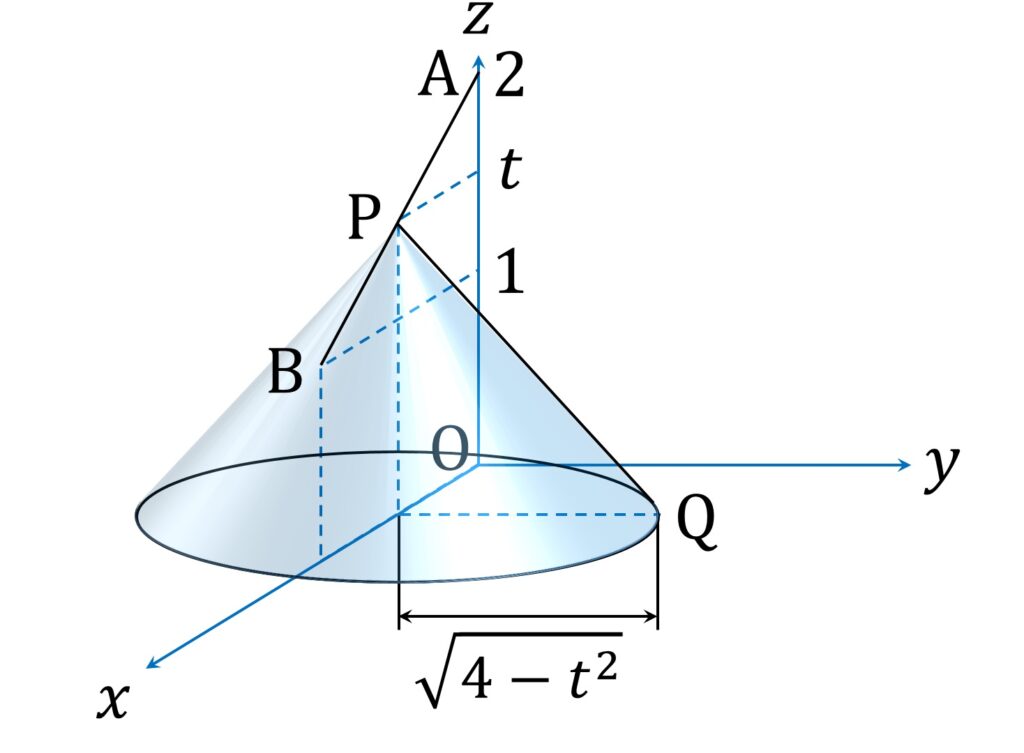
したがって、点 M は PQ の中点であることから、中心が (2-t,0, \frac{t}2) 、半径が \frac{\sqrt{ 4- t^2 }}2 の、 xy 平面に平行な平面 z = \frac{t}2 上の円周上にあります（図2）。
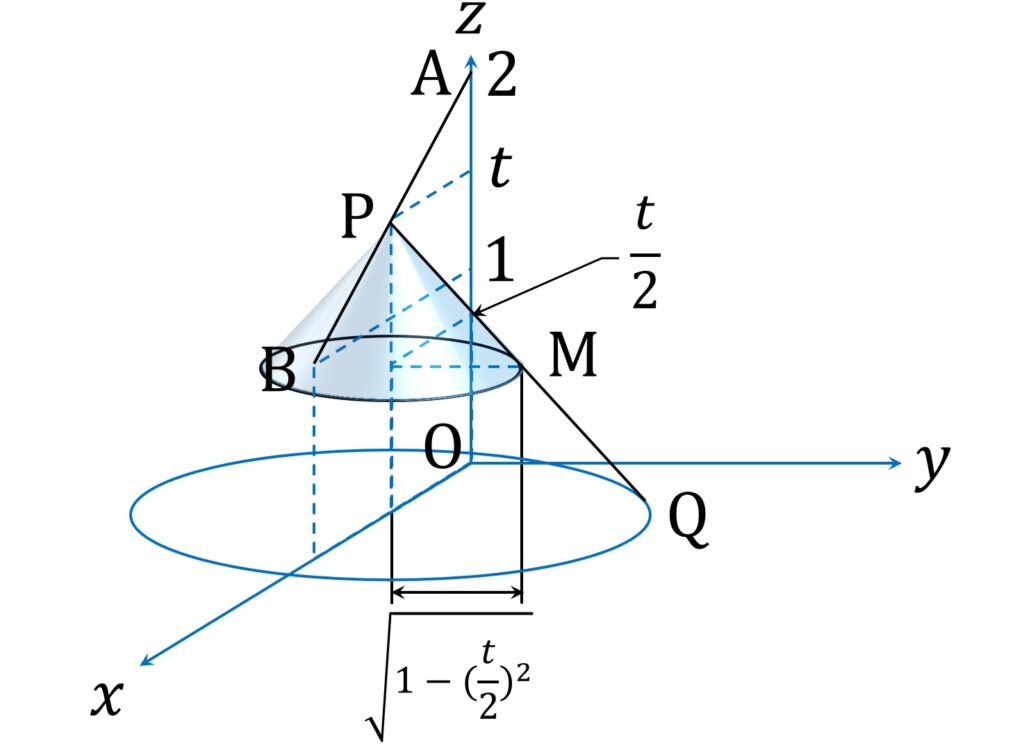
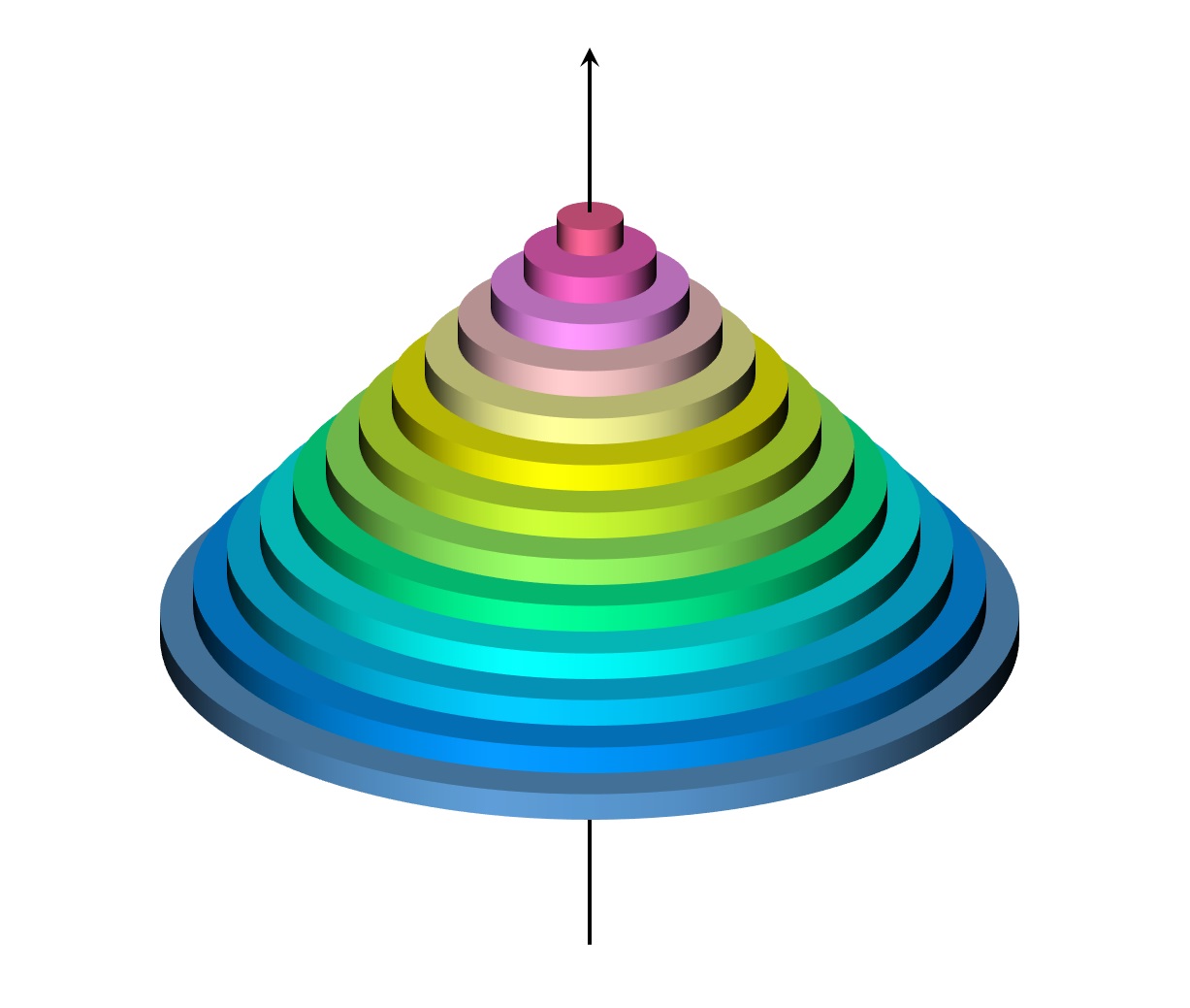
ここで図形全体を z 軸を中心に回転させると、点 M の存在領域は以下の円盤状領域になります（図3）。
