M の存在領域がドーナツ状であることの証明
東大の試験なので、図形に関する基本的な細かいことをそんなにくどくど説明しなくても大丈夫だと思いますが、 M が図6のドーナツ状領域に存在するのは必要条件であって、十分性は厳密には示されていません。念のため、以下、それを示します。
M が図7の位置に在るとします。
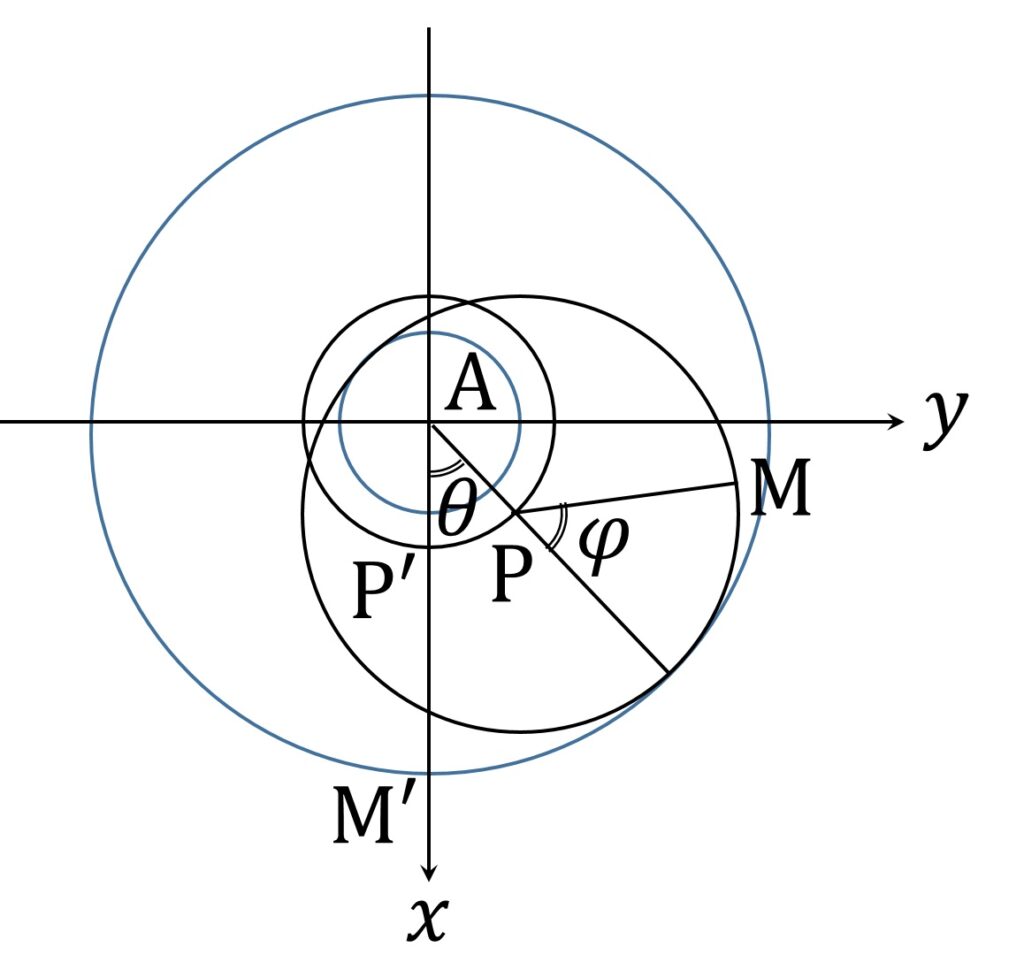
ここに 0 \leqq \theta, \phi < 2 \pi です。
M の座標を回転角で表現する
このとき、 \overrightarrow{\mathrm{AM} } は以下のように表記できます。
\begin{aligned}
\overrightarrow{\mathrm{AM} }=
\begin{pmatrix}
\cos (\theta + \phi) & -\sin (\theta + \phi) \\
\sin (\theta + \phi) & \cos (\theta + \phi)
\end{pmatrix}
\begin{pmatrix}
\frac{\sqrt{4-t^2}}{2}\\
0
\end{pmatrix} \\
+
\begin{pmatrix}
\cos \theta & - \sin \theta\\
\sin \theta &\cos \theta
\end{pmatrix}
\begin{pmatrix}
2-t \\
0
\end{pmatrix} \\
\cdots (1)
\end{aligned}
実際、 M は M’ を原点 A のまわりに角度θで回転し、次いで P のまわりに角度φで回転させたものですが、P のまわりに角度φで回転させるということは、
- - \overrightarrow{\mathrm{AP}} 方向に平行移動
- 原点A のまわりに角度φで回転
- \overrightarrow{\mathrm{AP}} 方向に平行移動
と同等です。そこで、ベクトル \overrightarrow{x} に対する原点 A を中心とした角度θの回転を R( \theta , \overrightarrow{x} ) と表記すると、
\small{
\begin{aligned}
\overrightarrow{ \mathrm{AM}} & =R(\phi, (R (\theta,\overrightarrow{ \mathrm{AM'}} ) -\overrightarrow{ \mathrm{AP}})) + \overrightarrow{ \mathrm{AP}} \\
& = R(\phi, (R (\theta,\overrightarrow{ \mathrm{AM'}} ) -R( \theta,\overrightarrow{ \mathrm{AP'}})) + R( \theta,\overrightarrow{ \mathrm{AP'}}) \\
& = R(\phi, (R (\theta,\overrightarrow{ \mathrm{AM'}}-\overrightarrow{ \mathrm{AP'}})) + R( \theta,\overrightarrow{ \mathrm{AP'}}) \\
& = R(\theta+\phi, \overrightarrow{ \mathrm{AM'}}-\overrightarrow{ \mathrm{AP'}}) + R( \theta,\overrightarrow{ \mathrm{AP'}}) \\
& = R(\theta+\phi, \overrightarrow{ \mathrm{M'P'}}) + R( \theta,\overrightarrow{ \mathrm{AP'}}) \\
\end{aligned}
}となります。
\overrightarrow{ \mathrm{M'P'}} =
\begin{pmatrix}
\frac{\sqrt{4-t^2}}{2}\\
0
\end{pmatrix},
\overrightarrow{ \mathrm{AP'}}=
\begin{pmatrix}
2-t \\
0
\end{pmatrix} なので、式(1)が示せました。
ここでドーナツ状領域の任意の点 X を
\mathrm{X} = (r \cos \alpha, r \sin \alpha) \\
\text{ここに} \\
-2+t + \frac{\sqrt{ 4- t^2 }}2 \leqq r \leqq 2-t + \frac{\sqrt{ 4- t^2 }}2\\
0 \leqq \alpha < 2 \piと表記するとき、任意の r, \alpha に対し、
\begin{aligned}
&
\begin{pmatrix}
\cos (\theta + \phi) & -\sin (\theta + \phi) \\
\sin (\theta + \phi) & \cos (\theta + \phi)
\end{pmatrix}
\begin{pmatrix}
\frac{\sqrt{4-t^2}}{2}\\
0
\end{pmatrix} \\
+ &
\begin{pmatrix}
\cos \theta & - \sin \theta\\
\sin \theta &\cos \theta
\end{pmatrix}
\begin{pmatrix}
2-t \\
0
\end{pmatrix} \\
= &
\begin{pmatrix}
r \cos \alpha \\
r \sin \alpha
\end{pmatrix}
\cdots (2)
\end{aligned}
を満たすθ、φが存在すれば、 M がドーナツ状領域に存在することの十分性が示されたことになります。