2022年東大 数学 第5問 の正しい解法
体積積分のおさらい
先の解法では、体積を求める図形 K を、xy 平面に平行な平面 z = \frac{t}2 でスライスした断面積の算出までは合っています。これを z 軸方向に積分せれば体積が算出できそうな気がしますが、ここに間違いが有ります。
そもそも、断面積の積分で体積が求められるのは、断面積が体積の導関数になっているからです。断面積および体積を t の関数と見立てて、それぞれ f(t),V(t) と表記し、 f(t) の連続性を仮定します。
ここで、 t が微小量 \Delta t 増加するとき、 ある 0 < \Delta t_0 < \Delta t が存在して、
V(t + \Delta t) - V(t) = \Delta t \cdot f(t+ \Delta t_0) \cdots(8)
が成り立ちます。
と、教科書には特に説明もなくしれっと書かれています(教科書では面積を対象にしていますが、体積でも原理は同じです)。しかし、直感的には理解できるものの、これは決して自明ではありません。
高校数学のこういうところがなんかモヤっとするというか、嘘くせーと感じるところですが、とりあえず式(8)を所与のものとして、話を進めます。
式(8)は \Delta t が負の場合でも成り立ちます。両辺を \Delta t で割って、
\frac{V(t + \Delta t) - V(t)}{\Delta t } = f(t+ \Delta t_0) \cdots(9)を得ます。 \Delta t \to 0 のとき、式(9)の右辺は、 f(t) が連続なので f(t) に収束します。よって、
\lim_{\Delta t \to0}\frac{V(t + \Delta t) - V(t)}{\Delta t } = f(t) \cdots(10)が成り立ちます。すなわち、 V(t) は微分可能であり、その導関数が f(t) に等しいことがわかりました。
正しい体積の求め方
ここで改めて、本問に戻ります。点 P の z 座標が \Delta t 増加するとき、 M は PQ の中点のため、その z 座標は \frac{\Delta t }2 増加します(図8)。
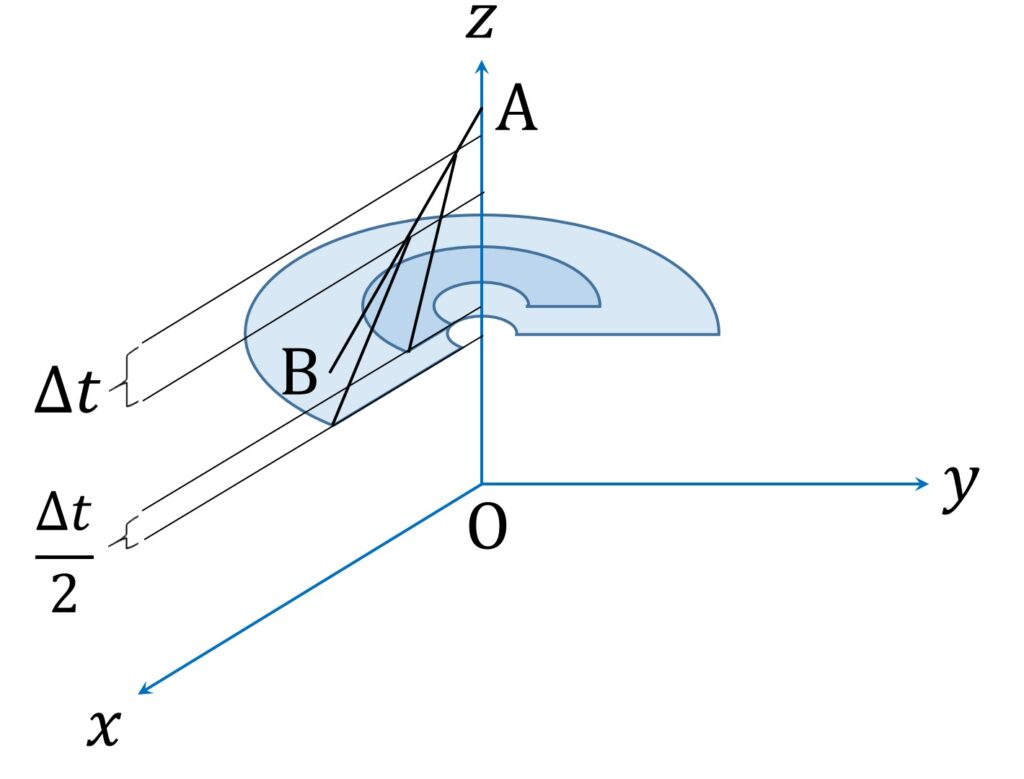
したがって式(8)は、以下のように書き換わります。
V(t + \Delta t) - V(t) = \frac{\Delta t}2 \cdot f(t+ \Delta t_0) \cdots (11)ゆえに V(t) の導関数 V'(t) は
V'(t) = \frac{1}2f(t) \cdots (12)を満たす、と言いたいところですが、式(8)の導出方法が不明なので、式(11)が正しいと言い切れません(直感的には明らかだし、実際に正しいのですが)。
そこで変数変換と合成微分の技法を適用します。
s = \displaystyle {\frac{t}2} と変数変換し、 g(s) = f(2s) と定義し、 g(s) の軌跡で生成される図形の体積を W(s) と表記します。 f(t) の軌跡と g(s) の軌跡は同じものなので、 明らかに W(s) = V(t) が成り立ちます。このとき、 g(s) には式(8)が適用出来るので、
W(s + \Delta s) - W(s) = \Delta s \cdot g(s+ \Delta s_0)
が成り立ちます。
よって、
\frac{d}{ds} W(s) = g(s)です。したがって、
\begin{aligned}
\frac{d}{dt} V(t) &= \frac{d}{ds} V(t) \cdot \frac{ds}{dt} \\
&=\frac{d}{ds} W(s) \cdot \frac{1}2 \\
&=\frac{1}2g(s) \\
&=\frac{1}2 f(2s) \\
&=\frac{1}2 f(t)
\end{aligned} となり、式(12)が示せました(やれやれ)。
今度こそ、体積が計算できます。 f(t) = 2\pi (2-t)\sqrt{ 4- t^2 } と置くとき、求める体積 V は
\begin{aligned}
V &= \int_1^2 V'(t) dt \\
& = \int_1^2 \frac{1}2f(t) dt \\
& = \int_1^2 \pi (2-t)\sqrt{ 4- t^2 } dt \\
& = 8 \pi \int_\frac{1}2^1 (1-s)\sqrt{ 1- s^2 } ds \\
& = -2 \sqrt{3} \pi+\frac{4 \pi^2}3
\end{aligned}となります。