2005年東大 数学 第2問 は複素数の問題ですが、題意が何を言っているのかわかりません。問題文は以下のとおりです。
| z | > \displaystyle\frac {5}4 となるどのような複素数zに対しても w = z ^2 - 2z とは表されない複素数w全体の集合をTとする。すなわち
T = \left \{ w \middle | w = z^2- 2z \text{ ならば } |z | \leqq \displaystyle\frac {5} 4 \right \}
とする。このとき、T に属する複素数wで絶対値 | w | が最大になるような w の値を求めよ。
いかがでしょうか。何か禅問答的と言うか、単なる音の連なりのようにも思えてきます。何度も読み返しているうちに、何かの呪文を唱えているような気分になってきます。
ただし、特にありがたいお経というわけでもないので、100遍唱えても悟りの境地に達したり、解けたりすることはありません。まずは、何を言っているのか理解するところから、始めましょう。
2005年東大 数学 第2問 の解法 Step1:集合Tの意味を理解する
まず最初に、集合Tがどんなものなのか、突き止めます。
w = z^2 -2z を満たす z は1つでないことに気付く
集合 T の定義が持って回った言い回しになっているのが本問のつまずきの石ですが、なぜ、
\left \{ w \middle | |z | \leqq \frac {5} 4 \text{である} z \text{が存在して} w = z^2 -2z\right \}といったわかりやすい表現になっていないのでしょうか。
これはもしかしたら、 w = z^2 -2z を満たす z は1つではなく、 | z | \leqq \frac{5}4 であるものと |z| > \frac{5}4 であるものの2種類がある場合がある、と言うことを意味しているのかもしれません。
そこで、 w = z^2 -2z を満たす複素数 z_1,z_2 があったとして、その関係を調べてみます。
z_1^2 -2z_1 = z_2^2 -2z_2
なので、右辺を左辺に移項して、
z_1^2 -2z_1 -z_2^2 +2z_2= 0
因数分解して
(z_1-z_2) (z_1 +z_2 -2)= 0
となります。
すなわち、 w = z^2 -2z を満たす複素数 z_1 があり、それとは別の複素数 z_2 があったとき、
z_ 2 = 2 - z_1
という関係が在ることがわかります。
複素数 z_1 が w = z^2 -2z を満たすとき、 2 -z_1 も満たすことに気付く
これから、 w = z^2 -2z なら w = (2-z)^2 -2(2-z) であることに気がつくことがポイントです。
実際、
\begin{aligned}
& (2-z)^2 -2(2-z) \\
= &4-4z+z^2 -4+2z \\
= & z^2 -2z = w
\end{aligned}です。
集合 T の”よりわかりやすい”定義を導出する
したがって、 w \in T ならば、 w = z^2 -2z を満たす z は
| z | \leqq \frac{5}4 \text{ かつ } |2-z| \leqq \frac{5}4を満たします。
よって、集合 T' を、
T' = \left \{ w \middle | \begin {aligned} & |z | \leqq \frac {5} 4 \text{ かつ } |2-z| \leqq \frac{5}4 \\
& \text{である} z \text{が存在して} w = z^2 -2z \end {aligned} \right \}と定義すると、 w \in T ならば w \in T' なのですから、
T \subseteqq T'
です。
一方、 w \in T' であるとします。このとき、 |z_1 | \leqq \frac {5} 4 \text{ かつ } |2-z_1| \leqq \frac{5}4 である z_1 が存在して、 w = z_1^2 - 2z_1 が成り立ちます。
ここでもし、 w = z_2^2 - 2z_2 を満たす z_2 が存在したとすると、 z_2 = z_1 または z_2 = 2 - z_1 なので、
| z_2 | \leqq \frac{5}4が成り立ちます。
すなわち、 w \in T' ならば、 w = z^2 - 2z を満たす z はすべて、 | z | \leqq \frac{5}4 を満たすので、 w \in T が成り立ちます。つまり、
T' \subseteqq T
です。
よって、
T' =T
であり、集合 T は
T = \left \{ w \middle | \begin {aligned} & |z | \leqq \frac {5} 4 \text{ かつ } |2-z| \leqq \frac{5}4 \\
& \text{である} z \text{が存在して} w = z^2 -2z \end {aligned} \right \}と表現できます。
2005年東大 数学 第2問 の解法 Step2:絶対値 |w| が最大になる w を求める
w \in T ならば、 | z | \leqq \frac{5}4 かつ |2-z| \leqq \frac{5}4 を満たす複素数 z が存在して、 w = z^2 -2z です。
このとき、
| w| = |z||2-z| \leqq \frac{25}{16}なので、
| z | = \frac{5}4 \text{ かつ } |2-z| = \frac{5}4を満たす z_0 が存在すれば、 w = z_0^2 -2z_0 が求める複素数です。
ところが、複素平面上の領域 \{ z \in \mathbb{C} | | z | \leqq \frac{5}4 かつ |2-z| \leqq \frac{5}4 \} を図示してみると明らかな通り、そのような z_0 は存在して、
z_0 = 1 \pm \frac{3}4 iです(図1)。
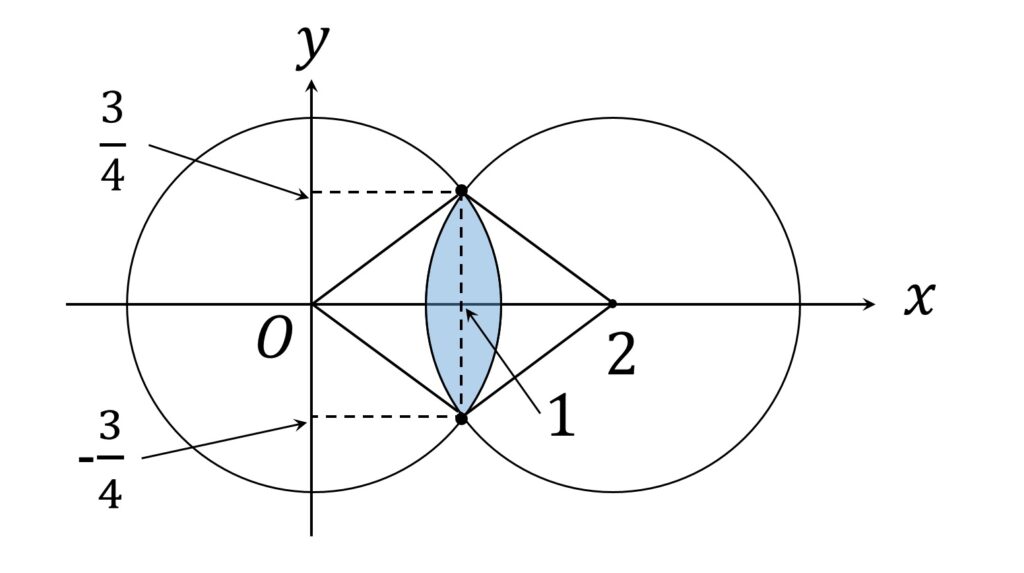
したがって求める w は
\begin{aligned}
w & = z_0^2 - 2 z_0 \\
& = z_0(z_0 -2) \\
& = (1 \pm \frac{3}4 i)(-1 \pm \frac{3}4 i) \text{ (複号同順)}\\
& = - \frac{25}{16}
\end {aligned}です。
解法のポイント

まず、集合 T が何なのか、理解することがポイントです。本稿に書いたように、妙に持って回った言い回しを手がかりにして、 w = z^2 -2z を満たす z は1つではなく、 | z | \leqq \frac{5}4 であるものと |z| > \frac{5}4 であるものの2種類があり得るということに気がつければ、集合 T の意味合いが見えてきます。
別のアプローチとして、 w = z^2 -2z を z の2次方程式に見立てるやりかたがあります。この視座に立てば、 z が複数(2つ)であることが直ちにわかります。
また、複素数の存在領域が定式化できたら、それを図示してみましょう。本稿に示したように、複素数の幾何学的側面を利用することによって、計算量と時間を節約できることがあります。
