2018年東大 数学 第6問 は、東大入試ではもはや名物と言える、変な形状の立体図形に関する問題です。問題文は以下のとおりです。
座標空間内の4点 O(0,0,0),A(1,0,0),B(1,1,0),C(1,1,1) を考える。
\displaystyle\frac{1}2 < r < 1 とする。点 P が線分 OA, AB, BC 上を動くときに点 P を中心とする半径 r の球(内部を含む)が通過する部分を、それぞれ V1,V2,V3 とする。
(1) 平面y = t が V1,V3 双方と共有点をもつような t の範囲を与えよ。さらに、この範囲の t に対し、平面 y = t と V1 の共通部分および、平面 y = t と V3 の共通部分を同一平面上に図示せよ。
(2) V1と V3 の共通部分が V2 に含まれるための r についての条件を求めよ。
(3) r は(2)の条件をみたすとする。 V1 の体積を S とし、 V1 と V2 の共通部分の体積を T とする。 V1,V2,V3 を合わせて得られる立体 V の体積を S と T を用いて表せ。
(4) ひきつづき r は(2)の条件をみたすとする。 S と T を求め、 V の体積を決定せよ。
いかがでしょうか。なんとも名状しがたい、謎問題です。まずは図形のイメージを掴みましょう。
まず V1,V2,V 3 ですが、太めのサラミソーセージ、またはボンレスハムみたいな形状です。

これが3本、直交するように配置されています(図1)。
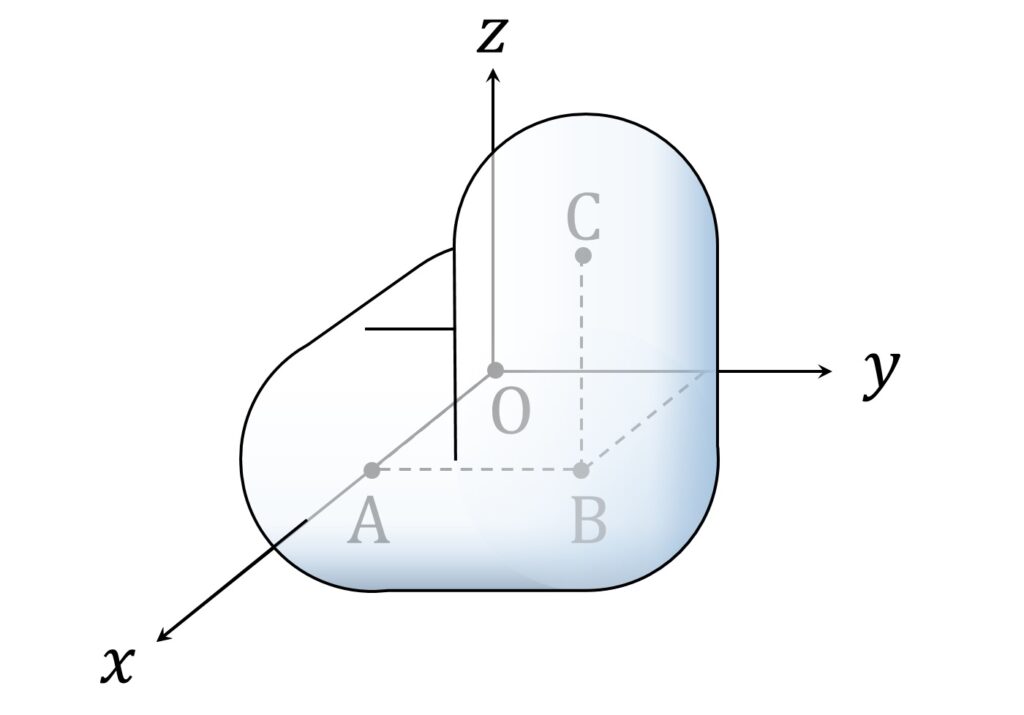
折れ曲がったフランクフルトソーセージみたいな形です。
なんとなくイメージがつかめたところで、問題に取り組みます。
2018年東大 数学 第6問 小問1の解法
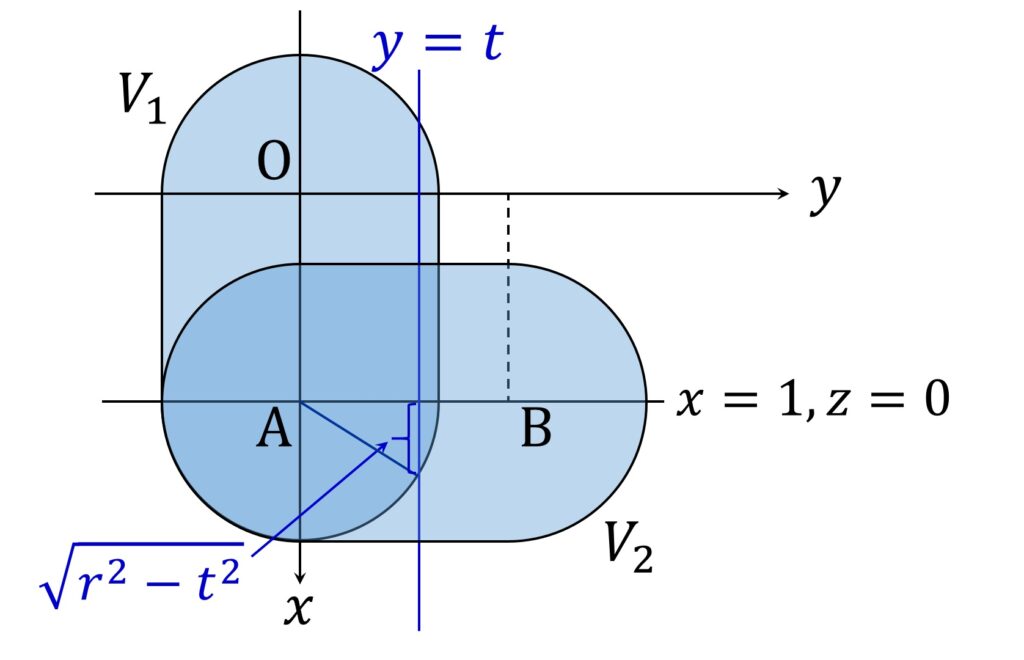
V1 と V3 を上(z軸の正方向)から見た図を描けば、求める t の範囲はすぐにわかります(図2)。
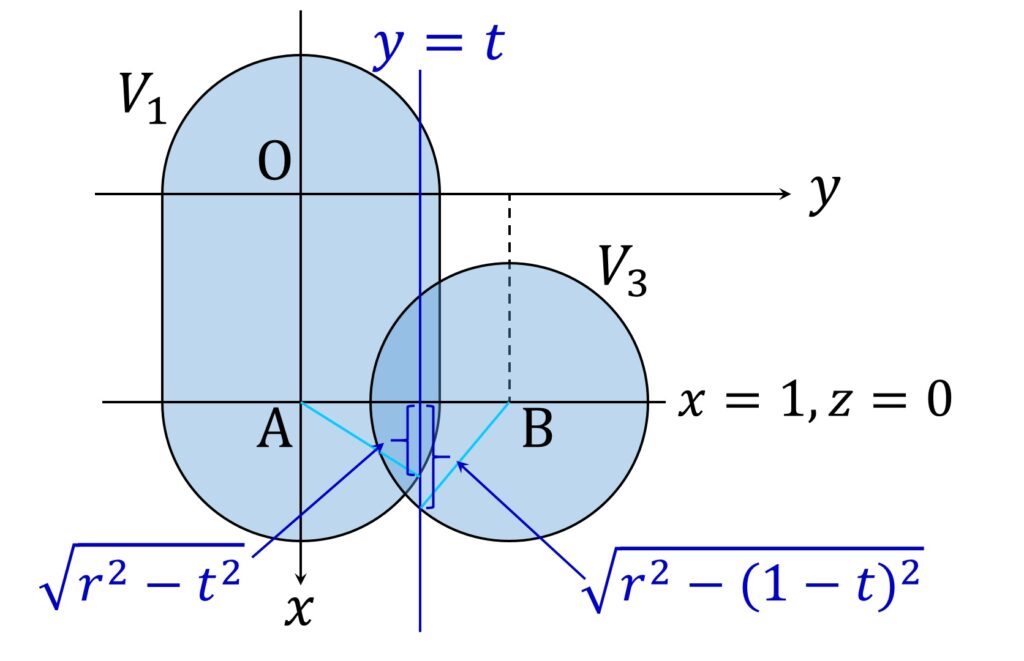
V1,V3 とも y 軸方向の幅が最大になる直線 x = 1, z = 0 上での V1 の存在範囲は -r \leqq y \leqq r 、V3 の存在範囲は 1-r \leqq y \leqq 1+r なので、 t の範囲は
1-r \leqq t \leqq r
です。
次に、断面図の描画です。
V1 V3 も、 y = t で切断した断面の形状は、円を2つに切ってその間を長方形で埋めた形です。それらが (x,z) = (1,0) で直行しています。
断面の円部分の半径は、 V1 の場合 \sqrt{ r^2 -t^2} , V3 の場合 \sqrt{ r^2 -(1 -t)^2 } です。
\displaystyle\frac{1}2 \leqq t \leqq r のとき、 \sqrt{ r^2 -t^2} \leqq \sqrt{ r^2 -(1 -t)^2 } なので、 V1 と V3 の共通部分の断面は、y 軸の正方向から見たとき、図3のようになります。
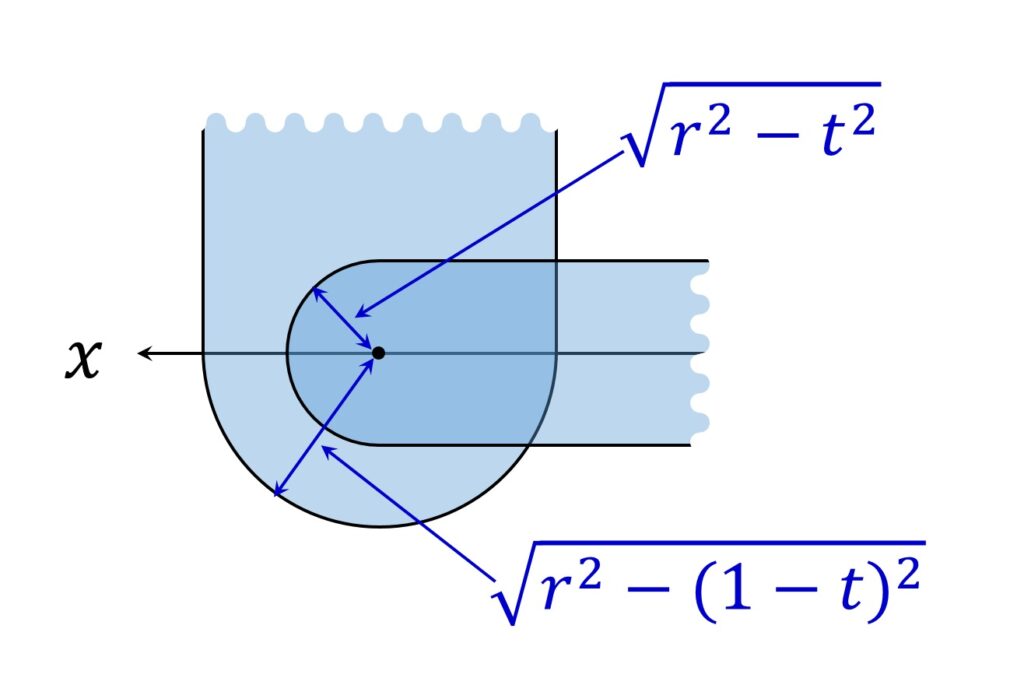
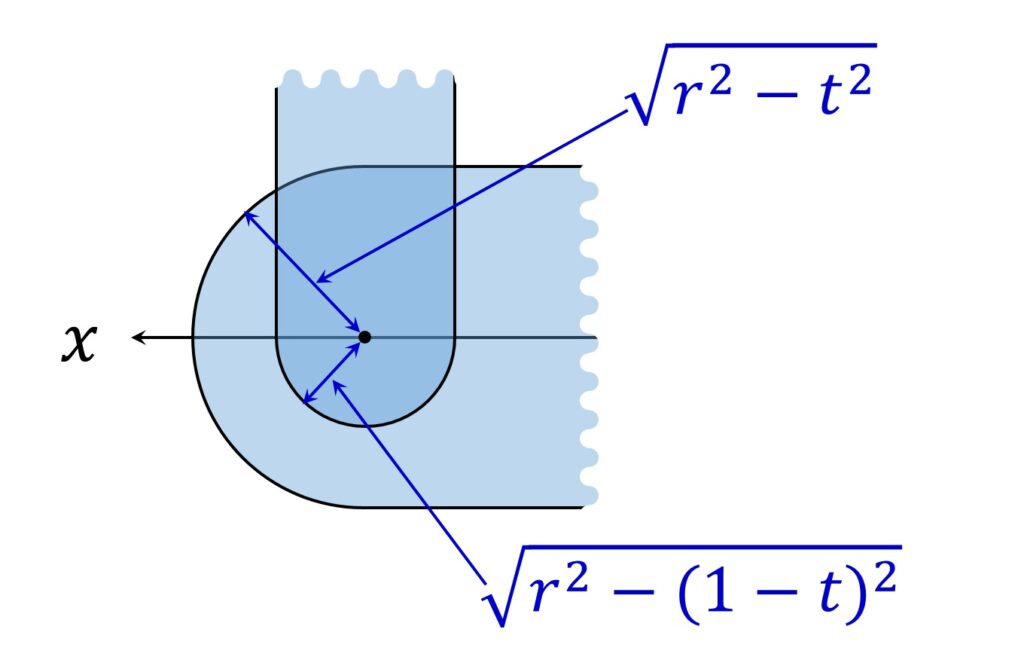
また、 1 -r \leqq t < \displaystyle\frac{1}2 のとき、 \sqrt{ r^2 -(1 -t)^2 }< \sqrt{ r^2 -t^2} なので、 V1 と V3 の共通部分の断面は、y 軸の正方向から見たとき、図4のようになります。
2018年東大 数学 第6問 小問2の解法
V1 と V3 の共通部分の y 軸方向の存在範囲は、小問1で見たように、 1-r \leqq t \leqq r です。これは V2 の円筒部分に含まれますので、V1 と V3 の共通部分が V2 に含まれる必要十分条件は、 1-r \leqq t \leqq r であるすべての t に対し、小問1で作成した共通部分の断面図が (x,z) = (1,0) を中心とする半径 r の円に含まれることです。
ところが、断面の図形の各点と (x,z) = (1,0) との距離の最大値は、
\begin{aligned}
& \sqrt{r^2-t^2+ r^2- (1-t)^2} \\
= & \sqrt{2 r^2 - \frac{1}2 - 2 \left( t-\frac{1}2 \right)^2}
\end{aligned}です(図5)。
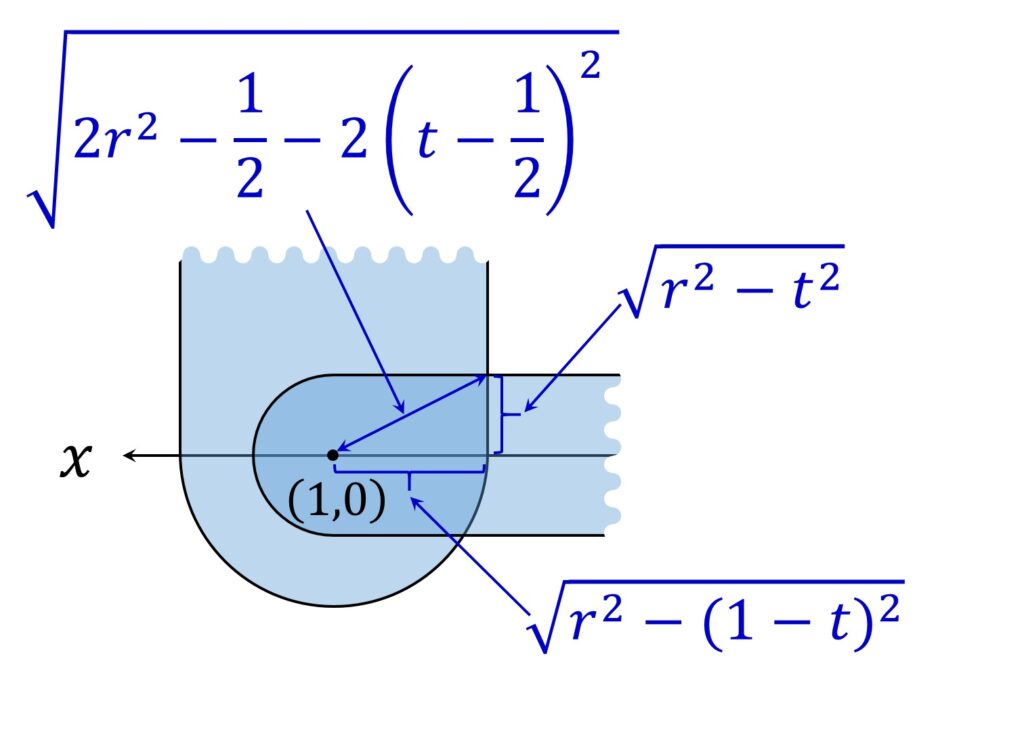
すべての 1-r \leqq t \leqq r に対して
\begin{aligned}
\sqrt{2 r^2 - \frac{1}2 - 2 \left( t-\frac{1}2 \right)^2} \leqq r
\end{aligned}が成り立てばよいわけですが、左辺は t = \displaystyle\frac{1}2 のとき、最大値 \sqrt{2 r^2 - \frac{1}2 } を取るので、V1 と V3 の共通部分が V2 に含まれる必要十分条件は
\begin{aligned}
\sqrt{2 r^2 - \frac{1}2 } \leqq r
\end{aligned}が成り立つことです。
両辺を2乗して
\begin{aligned}
2 r^2 - \frac{1}2 \leqq r^2
\end{aligned}ですが、 \displaystyle\frac{1}2 < r < 1 であったので、
\frac{1}2 < r \leqq \frac{\sqrt 2 }2であることが、V1 と V3 の共通部分が V2 に含まれる必要十分条件です。
2018年東大 数学 第6問 小問3の解法
こういう問題の時は、ベン図を書いて整理するのが吉です。
\begin{aligned}
& V_1 \cup V_2 \cup V_3 \\
= & V_1 \backslash (V_1 \cap V_2) \backslash \{ (V_1 \cap V_3) \backslash ( V_1 \cap V_2 \cap V_3)\} \\
& \cup V_3 \backslash (V_3 \cap V_2) \backslash \{ (V_1 \cap V_3) \backslash ( V_1 \cap V_2 \cap V_3) \} \\
& \cup V_2
\end{aligned}ですが、V1と V3 の共通部分が V2 に含まれる、すなわち
V_1 \cap V_3 \subset V_2
なので、
(V_1 \cap V_3 ) \backslash ( V_1 \cap V_2 \cap V_3) = \empty
です(図6)。
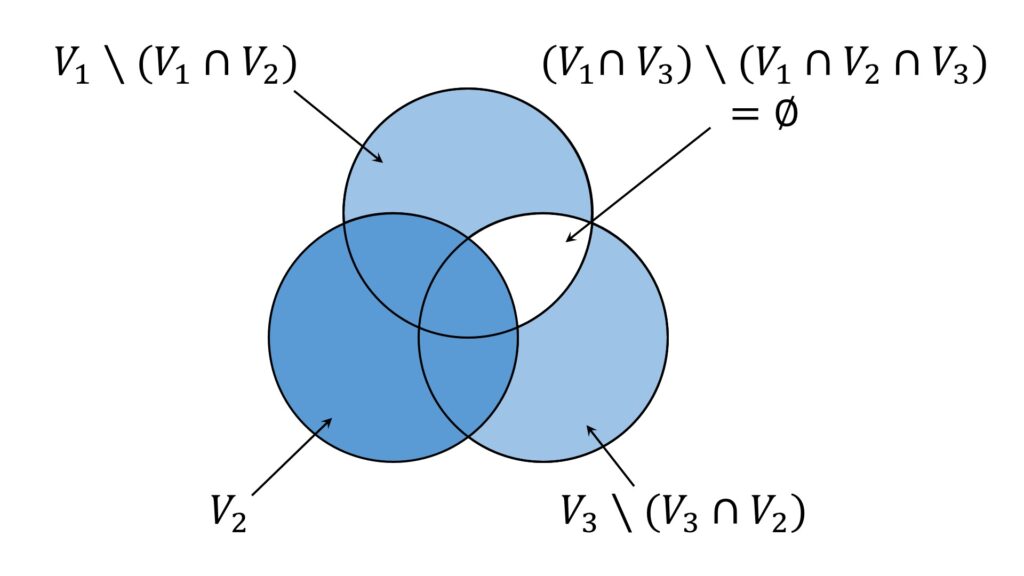
したがって、
\begin{aligned}
& V_1 \cup V_2 \cup V_3 \\
= & \{V_1 \backslash (V_1 \cap V_2) \} \cup \{V_3 \backslash (V_3 \cap V_2) \} \cup V_2
\end{aligned}が成り立ちます。
ここで立体図形 F の体積を m(F) と表記するとき、
\begin{aligned}
& m(V_1 \cup V_2 \cup V_3 ) = V \\
& m(V_1) = m(V_2) = m (V_3) = S \\
\end{aligned}ですが、図形の対称性より
\begin{aligned}
m (V_1 \cap V_2 ) = m (V_3 \cap V_2 )= T \\
\end{aligned}です。よって、
\begin{aligned}
V = & m( V_1 \cup V_2 \cup V_3) \\
= & m(V_1 \backslash (V_1 \cap V_2) \cup V_3 \backslash (V_3 \cap V_2) \cup V_2 ) \\
= & m(V_1 \backslash (V_1 \cap V_2) ) +m( V_3 \backslash (V_3 \cap V_2) ) \\
& + m( V_2) \\
= & m(V_1) - m( V_1 \cap V_2 ) \\
&+ m(V_3) - m( V_3 \cap V_2 ) \\
&+ m(V_2) \\
= & 3S -2T
\end{aligned}が成り立ちます。
2018年東大 数学 第6問 小問4の解法
まず、 S の体積は簡単に求められます。半径 r の球と底面の半径が r 、高さが 1 の円柱の和なので、
\frac{4}3 \pi r^3 + \pi r^2です。
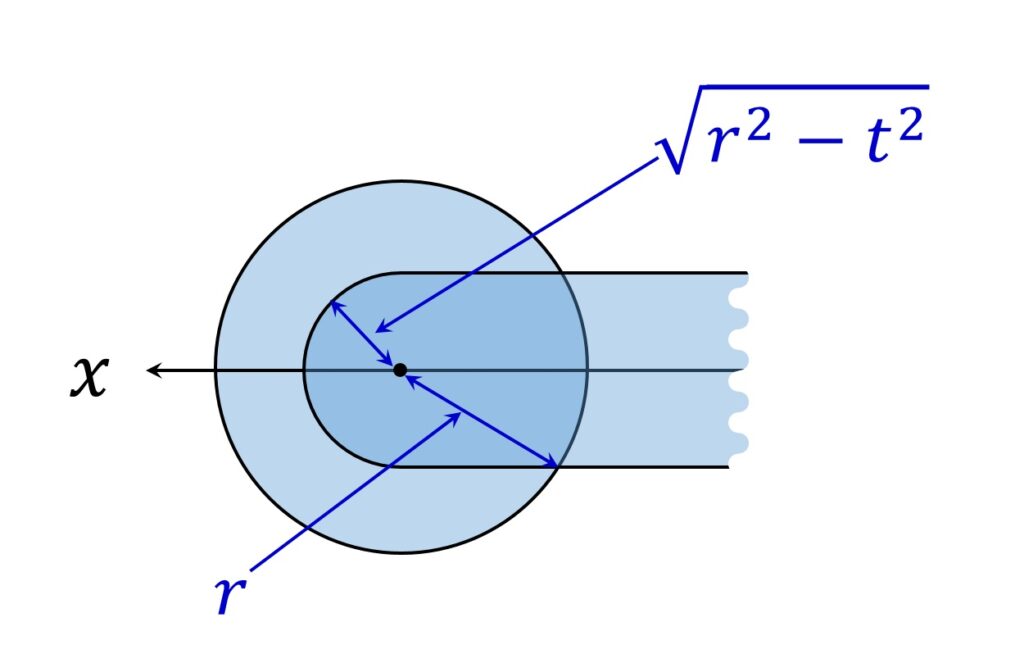
問題は T のほうです。上( z 軸の正方向)から見た図を描いてみます(図7)。
T を平面 y = t でスライスした断面の面積を、 y 軸方向に積分すれば T の体積が求められます。
ところが、 t ≦ 0 の範囲で T は半径 r の半球なので、その体積は \displaystyle\frac{2}3 \pi r^3 です。よって、 t > 0 の範囲だけを考えればよいことがわかります。
t > 0 のときのT を平面 y = t でスライスした断面を、 y 軸の正方向から見た形状は以下の通りです(図8)。
この図形を以下のように3種類に分割します(図9)。
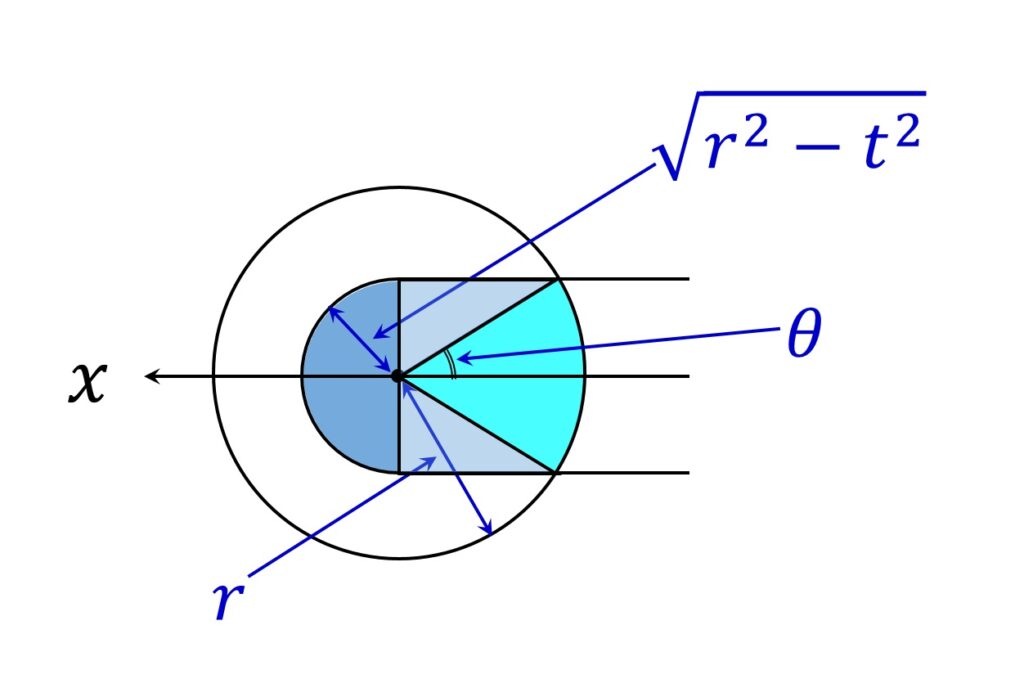
各部の面積は以下の通りです。
\begin{aligned}
\text{半円} & = \frac{ \pi}2 ( r^2 -t^2) \\
\text{三角形} & = t \sqrt{r^2 -t^2} \\
\text{扇形} & = \ \theta r^2
\end{aligned}ここに θ は図9のθで、 t の関数です。θ の値の範囲は 0 \leqq \theta < \frac{\pi}2 です。 t と θ の間には以下の関係があります。
\sin \theta = \frac{ \sqrt { r^2 - t^2}}r以下、各部の体積を積分して求めます。
半円部分の体積
実は半円部分は半径 r の球を4等分したものなので、体積は積分するまでもなく \displaystyle\frac{ \pi r^3}3 であることがわかります。
三角形部分の体積
求める体積は
\int_0^r t \sqrt{r^2-t^2} dtですが、 t = r \sin \varphi と変数変換すると、
\frac{dt}{d \varphi} = r \cos \varphiであることから、
\begin{aligned}
& \int_0^r t \sqrt{r^2-t^2} dt \\
= & \int_0^{\frac{\pi}2 } r \sin \varphi \cdot \sqrt{ r^2 - r^2 \sin ^2 \varphi } \cdot r \cos \varphi d \varphi \\
= & r^3 \int_0^{\frac{\pi}2 } \cos ^2 \varphi \sin\varphi d \varphi \\
= &- \frac{r^3 }3 [ \cos^3 \varphi ]_0^{\frac{\pi}2 } \\
= & \frac{r^3 }3
\end{aligned}です。
扇型部分の体積
こいつが少々クセモノです。求める体積は、 θ を t の関数に見立てて
r^2 \int_0^r \theta dt
を計算すれば求められます。arcなんたら関数の原始関数を覚えていれば一発ですが、そんなのを知らなくても、変数変換で突破できます。
\sin \theta = \frac{ \sqrt { r^2 - t^2}}rであったので、分母を払って両辺を2乗すると
r^2 \sin^2 \theta = r^2 -t^2
です。よって、
\begin{aligned}
t^2 & = r^2- r^2 \sin^2 \theta \\
& = r^2 \cos ^2 \theta
\end{aligned}ですが、 t > 0 なので、
t = r \cos \theta
です。したがって
\frac{dt }{d \theta}= -r \sin \thetaなので、
\begin{aligned}
& r^2 \int_0^r \theta dt \\
= & r^2 \int_{\frac{\pi}2}^0 \theta(-r \sin \theta) d \theta \\
= & r^3 \int_0^{ \frac{\pi}2} \theta \sin \theta d \theta \\
= & -r^3 [ \theta \cos \theta]_0^{ \frac{\pi}2} + r^3 \int_0^{ \frac{\pi}2} \cos \theta d \theta \\
= & r^3
\end{aligned}です。
結論
上記の計算により、
\begin{aligned}
T & = \frac{2\pi r^3} 3 + \frac{\pi r^3} 3 + \frac{r^3}3 +r^3 \\
& =\pi r^3+ \frac{4r^3}3
\end{aligned}なので、求めるV は
\begin{aligned}
V = & 3S -2T \\
= & 3 \left (\frac{4 \pi r^3}3 + \pi r^2 \right) -2 \left (\pi r^3+\frac{4 r^3}3 \right ) \\
= & 2 \pi r^3 + 3 \pi r^2 - \frac{8 r^3}3
\end{aligned}となります。
解法のポイント

本問のような謎図形の問題の場合は、セオリー通り平面図を描いて、全体的なイメージをつかむようにしましょう。本問の場合は平面図が円と長方形で構成されているため、思ったより単純な図形であることがわかります。
本問の最大の難所は小問3です。ぱっと見、どうすりゃいいのか見当もつきませんが、本稿で示したとおり、本問を集合の問題と捉えてベン図を書いてみると状況が整理できます。図6が描けて、条件より (V_1 \cap V_3 ) \backslash ( V_1 \cap V_2 \cap V_3) = \empty であることに気がつければ、一気に答えにたどり着けることでしょう。
小問4も一瞬あせりますが、変数変換すれば良いことに気がつければ、どうということはありません。そこそこの難易度でいいので、積分の問題をたくさん解いて、感覚を養うようにしましょう。
