トランプシャッフル後のカードの並び順 – 2002年東大 数学 第6問

2023年12月13日2023年12月14日

発展：カード枚数が2のべき乗でない場合

　カード枚数が2のべき乗の場合は、いい感じにカードの並びが元に戻ることを示せましたが、カード枚数が2のべき乗でない場合はどうなるのか、考えてみましょう。

　カード枚数が 2N のとき、小問2の結果より、 f(k) -2k が 2N + 1 で割り切れるので、 2N + 1 に関する場合分けで考えてみます。

2N + 1 が素数に等しいとき

　2N + 1 = p (p は3以上の素数） のとき、フェルマーの小定理というものがあって、任意の自然数 k に対し

k^{p} \equiv k ( \mod p)

が成り立ちます。

　証明は以下のとおりです。そんなに難しくないし、証明手法が結構役に立つので、考え方を覚えておきましょう。

　2項定理を利用します。

\begin{aligned}
k^p  & =   \{ (k-1)+1 \}^p \\
 & = \sum_{i=0}^p  {}_{p} \mathrm{C}_i (k-1)^{p-i} \\
 & = (k-1)^p +\sum_{i=1}^{p-1}  {}_{p} \mathrm{C}_i (k-1)^{p-i} \ +1\
\end{aligned}

が成り立ちますが、 1 ≦ i ≦ p-1 のとき

{}p \mathrm{C}_i = \frac{p!}{(p-i)!i!}

の分母はすべて素数 p と素なので、分子の p は約分されません。よって _pC_i は p の約数であり、

\begin{aligned}
k^p & \equiv (k-1)^p +1 \\
 & \equiv (k-2)^p+2 \\
 &  \text{　　} \vdots \\
 & \equiv 1^p +(k-1)  \\
 & \equiv k ( \mod p)
\end{aligned}

が成り立ちます。

　k が p と素なとき、

k^{p-1} \equiv 1 ( \mod p)

が成り立ちます。

k^p -k = k( k^{p-1} -1) \equiv 0 ( \mod p)

が成り立ちますが、 k は p と素なので k^p-1 – 1 は p の倍数でなければなりません。ゆえに

k^{p-1} - 1 \equiv 0 ( \mod p)

すなわち

k^{p-1} \equiv 1 ( \mod p)

です。

　特に、

2^{p-1} \equiv 1 ( \mod p)

です。よって1 ≦ k ≦ 2N のとき

\begin{aligned}
f_{p-1} (k) \equiv 2^{p-1}k \equiv k ( \mod p)
\end{aligned}

が成り立ちますが、1 ≦ f_p-1(k) ≦ 2N なので

\begin{aligned}
f_{p-1} (k) = k
\end{aligned}

が成り立ちます。

　 p -1 は 2N すなわちカードの枚数なので、カード枚数回シャッフルすると、元の並びに戻ることになります。たとえばカードが4枚のとき、

と、確かに4回のシャッフルで元の並びに戻ります。また、ジョーカーを除いたトランプ一式の枚数は52枚であり、 52+1=53 は素数なので52回シャカシャカとシャッフルすれば、元の並びに戻ることになります。

2N + 1 が素数の積に等しいとき

　2N + 1 =pq（p,q は3以上の素数）であるとします。任意の自然数 k に対し k^{p-1} \equiv 1 ( \mod p) 、 k^{q-1} \equiv 1 ( \mod q) なので、

k^{(p -1)(q-1) }  \equiv 1 ( \mod pq)

が成り立つことが予想できます。

　実際、フェルマーの小定理により、

k^{(p -1)(q-1) } = (k^{p-1})^{q-1}\equiv 1 ( \mod q)

なので、ある整数 a が存在して、

k^{(p -1)(q-1) }= 1 +aq

が成り立ちます。

　同様に、

k^{(p -1)(q-1) } = (k^{q-1})^{p-1}\equiv 1 ( \mod p)

なので、ある整数 b が存在して、

k^{(p -1)(q-1) }= 1 +bp

が成り立ちます。

　よって、

aq=bp

が成り立ちますが、

a= \frac{bp}q

で、かつ a が整数、かつ p,q は互いに素なので、 b は q で割り切れます。したがって、ある整数 c が存在して

 b= cq

が成り立つので

k^{(p -1)(q-1) }= 1 +cpq

すなわち

k^{(p -1)(q-1) } \equiv  1 (\mod pq)

が成り立ちます。

　特に

2^{(p -1)(q-1) } \equiv  1 (\mod pq)

　なので1 ≦ k ≦ 2N のとき、

\begin{aligned}
f_{(p-1)(q-1)}(k)  & \equiv 2^{(p-1)(q-1)}k \\
 & \equiv k (\mod pq)

\end{aligned}

ですが、1 ≦ f_(p-1)(q-1)(k) ≦ 2N なので

\begin{aligned}
f_{(p-1)(q-1)}(k) =k 

\end{aligned}

であり、 (p-1)(q-1) 回シャッフルすると、元の並びに戻ります。

2N + 1 が互いに素な2つの奇数の積に等しいとき

　2N + 1 =pq（p,q は3以上の奇数）でかつ、ある自然数 i,j が存在して、すべての自然数 k に対し

\begin{aligned}
k^i & \equiv 1 ( \mod p) \\
k^j & \equiv 1 ( \mod q)
\end{aligned}

が成り立つとします。

　このとき、 p,q が素数の場合と同様に、

k^{ij }  \equiv 1 ( \mod pq)

が成り立ちます。

　仮定より、

k^{ij } = (k^{i})^{j}\equiv 1 ( \mod q)

なので、ある整数 a が存在して、

k^{ij }= 1 +aq

が成り立ちます。

　同様に、

k^{ij } = (k^{j})^{i}\equiv 1 ( \mod p)

なので、ある整数 b が存在して、

k^{ij }= 1 +bp

が成り立ちます。

　よって、

aq=bp

が成り立ちますが、

a= \frac{bp}q

で、かつ a が整数、かつ p,q は互いに素なので、 b は q で割り切れます。したがって、ある整数 c が存在して

 b= cq

が成り立つので

k^{ij }= 1 +cpq

すなわち

k^{ij } \equiv  1 (\mod pq)

が成り立ちます。

　したがって 1 ≦ k ≦ 2N のとき、 p,q が素数の場合と同様に

\begin{aligned}
f_{ij}(k)  & \equiv 2^{ij}k \\
 & \equiv k (\mod pq)

\end{aligned}

が成り立ちますが、1 ≦ f_ij(k) ≦ 2N なので、

\begin{aligned}
f_{ij}(k) =k 

\end{aligned}

であり、 ij 回シャッフルすると、元の並びに戻ります。

　以上の内容は明らかに、 1+2N が3つ以上の互いに素な数に因数分解できる場合にも成り立ちます。よって

1+2N = p_1p_2 \cdots p_m \\
(p_1,p_2, \cdots , p_m \text{は互いに異なる素数})

のとき、 (p₁-1)(p₂-1) …(p_m-1) 回のシャッフルで元の並びに戻ることがわかります。

2N + 1 が3以上の素数のべき乗に等しいとき

　次に、2N + 1 =p^m（p は3以上の素数、 m ≧ 2）の時にどうなるかを考えます。任意の自然数 k に対し

\begin{aligned}
k^{p-1} & \equiv 1 ( \mod p) \\

\end{aligned}

なので

\begin{aligned}
k^{(p-1)^m} & \equiv 1 ( \mod p^m) \\

\end{aligned}

が成り立つと予想できますが、実際の数字で確かめましょう。

　p=3,m=2,k=2 の場合で調べます。すると

2^{2^2} = 16 \equiv 7 ( \mod 9)

なので、予想は外れました。

　そもそも小問3により、 2N = 2³=8 のとき、f₆(1)=1 です。小問2により

f_6(1) -2^6 \times1 \equiv0 ( \mod 9)

なので、

2^6  \equiv 1 ( \mod 9)

です。 6= (3-1)× 3 なので、もしかしたら

\begin{aligned}
k^{p(p-1)} & \equiv 1 ( \mod p^2) \\

\end{aligned}

が成り立つかも知れません。これを確かめてみます。

　任意の自然数 k に対し

\begin{aligned}
k^{p-1} & \equiv 1 ( \mod p) \\

\end{aligned}

なので、ある整数 a が存在して

\begin{aligned}
k^{p-1} = 1 +ap \\

\end{aligned}

が成り立ちます。

　よって

\begin{aligned}
k^{p(p-1)} & = (1 +ap)^p \\
 & =  \sum_{i=0}^p {}_p \mathrm{C}_i (ap)^i \\
 & = 1 + ap^2 + \sum_{i=2}^p {}_p \mathrm{C}_i (ap)^i

\end{aligned}

ですが（ _pC₁=p に注意）、右辺の１以外の項は明らかに p² の倍数なので、

\begin{aligned}
k^{p(p-1)} & \equiv 1 ( \mod p^2) \\

\end{aligned}

が証明できました。

　この結果を一般化すると、 m ≧ 2 のとき

\begin{aligned}
k^{(p-1)p^{m-1}} & \equiv 1 ( \mod p^m) \\

\end{aligned}

が成り立ちそうです。以下、これを m に関する数学的帰納法で証明します。

　 m=2 のときは証明済みです。 m=l ( l ≧ 2) のとき、

\begin{aligned}
k^{(p-1)p^{l-1}} & \equiv 1 ( \mod p^l) \\

\end{aligned}

　が成り立っていると仮定します。このとき、ある整数 a が存在して

\begin{aligned}
k^{(p-1)p^{l-1}} = 1 +ap^l \\

\end{aligned}

が成り立ちます。よって、

\begin{aligned}
k^{(p-1)p^l} & = (k^{(p-1)p^{l-1} })^p \\
 & =(1 +ap^l)^p \\
 & =  \sum_{i=0}^p {}_p \mathrm{C}_i (ap^l)^i \\
 & = 1 + ap^{l+1} + \sum_{i=2}^p {}_p \mathrm{C}_i (ap^l)^i

\end{aligned}

ですが、右辺の１以外の項は明らかに p^l+1 の倍数なので、

\begin{aligned}
k^{(p-1)p^l} & \equiv 1 ( \mod p^{l+1}) \\

\end{aligned}

が成り立ちます。ゆえに m ≧ 2 のとき

\begin{aligned}
k^{(p-1)p^{m-1}} & \equiv 1 ( \mod p^m) \\

\end{aligned}

が成り立つことが証明できました。

　特に

\begin{aligned}
2^{(p-1)p^{m-1}} & \equiv 1 ( \mod p^m) \\

\end{aligned}

なので、

\begin{aligned}
f_{(p-1)p^{m-1}}(k)  & \equiv 2^{(p-1)p^{m-1}}k \\
 & \equiv k (\mod p^m)

\end{aligned}

が成り立ちますが、 1 \leqq f_{(p-1)p^{m-1}}(k) \leqq 2N なので、

\begin{aligned}
f_{(p-1)p^{m-1}}(k)  = k 

\end{aligned}

であり、 (p-1)p^m-1回シャッフルすると、元の並びに戻ります。

2N + 1 が一般の奇数のとき

　以上をまとめると、 2N + 1 が以下のように素因数分解できるとき、

1+2N = p_1^{\alpha_1}p_2 ^{\alpha_2} \cdots p_m ^{\alpha_m} \\
  \left ( \begin{aligned} & p_1,p_2, \cdots ,p_m \text{は互いに異なる素数} \\
  & \alpha_1,\alpha_2, \cdots ,\alpha_m \text{は自然数} \end{aligned}  \right)

(p_1-1) p_1^{\alpha_1-1}(p_2-1) p_2^{\alpha_2-1} \cdots (p_m-1) p_m^{\alpha_m-1} 回シャッフルすると、元の並びに戻ることがわかりました。

2N + 1 が素数 p に等しく、かつ p-1 より小さい自然数 m が存在して　p +1 = 2^m のとき

　カードの枚数が何枚であっても、偶数ならば元の並びに戻るシャッフルの回数を求めることが出来ました。しかし、もっと少ない回数で元に戻らないか、考えてみることにします。

　フェルマーの小定理により、

2^{p-1} \equiv 1 ( \mod p)

が成り立ちますが、 p の値によっては、 p-1 より小さい自然数 m に対して

2^{m} \equiv 1 ( \mod p)

すなわち

p+1 = 2^m

が成り立つことが有ります。たとえば p = 7 のとき、

2^{3} = 8 \equiv 1 ( \mod 7)

です。

　このような条件を満たすとき、

\begin{aligned}
f_{m}(k)  & \equiv 2^mk \\
 & \equiv k (\mod p)

\end{aligned}

が成り立ちますが、 例によって 1 \leqq f_m(k) \leqq 2N なので、

\begin{aligned}
f_{m}(k)  = k 

\end{aligned}

すなわち、 m 回のシャッフルによって元の並びに戻ります。

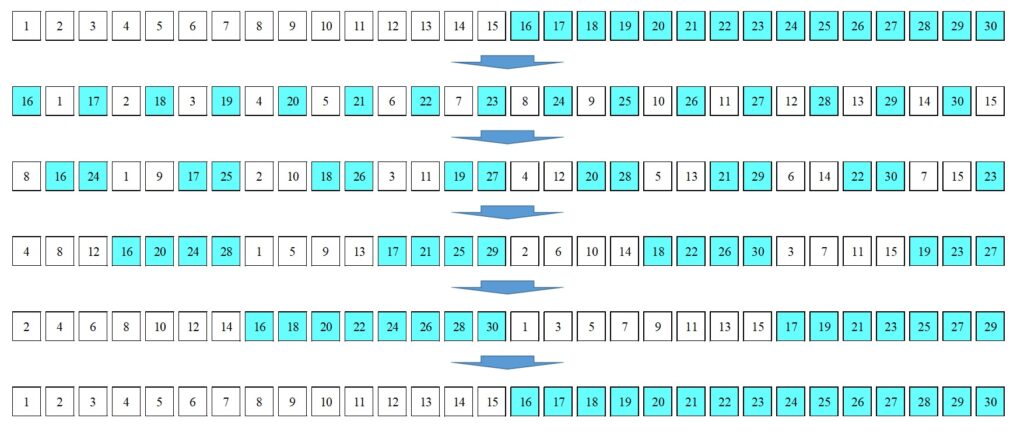
　実際に p=7 の場合で確認してみましょう。

1,2,3,4,5,6
↓
4,1,5,2,6,3
↓
2,4,6,1,3,5
↓
1,2,3,4,5,6

と、確かに３回のシャッフルで元の並びに戻りました！

　この結果により、例えばカード枚数が３０枚のとき、30 + 1 = 31 で素数であり、しかも 31 + 1 = 32 = 2⁵ なので、わずか5回のシャッフルで元の並びに戻ることがわかります。つまり、シャッフルによって作り出されるカードの並びは、5種類しか無いということです(図１)。カードのシャッフルってカードの並びをもっとランダムにできるものだと思っていましたが、全然そうではないので驚きです。奇術のタネに使われているのではないかと思いました。

解法のポイント

　本問は小問で設問になれたうえで本題に取り組むという、親切設計になっています。しかもそのために用意された小問1および小問2が簡単なので、これらは必ず得点するようにしましょう。

　小問3は素数の剰余類で無いところがいささか不安ですが、小問1をヒントに n 回のシャッフルでカードの並びが反転することに気がつければ、小問2の 2N+1 の剰余類というのがものすごく効いてきて、本稿に示したように比較的さくっと解けることと思います。

　これに気が付けなくても、剰余類の計算がちょっとだけ面倒くさくなるだけで、答えを導き出すことは出来ます。

　本問はむしろ、「発展」で示したように、カード枚数がより一般的な場合にどうなるかのほうが、骨があって入試問題向きです。フェルマーの小定理が前提になっているので出題は難しいと思いますが、回答の量は多いものの無理なく解けるので、履修範囲の問題がなければ出題されていたかも知れません。剰余類の扱い方の参考になりますので、できればさらっておいてください。