正射影の難問を定性的に何とかする – 1988年東大 数学 第2問
1988年東大 数学 第2問 は正四面体の正射影面積の最大値、最小値を求める問題です。問題文は以下のとおりで、東大第2次試験問題からの引用です。
空間内に平面 α がある。一辺の長さ1の正四面体 V の α 上への正射影の面積を S とし、 V がいろいろと位置を変えるときの S の最大値と最小値を求めよ。
ただし、空間の点 P を通って α に垂直な直線が α と交わる点を P の α 上への正射影といい、空間図形 V の各点の α 上への正射影全体のつくる α 上の図形を V の α 上への正射影という。
この手の問題はベクトルなどを使って正射影の面積を数式として求め、それを微分して最大、最小値を求めるというアプローチが一般的ですが、本問はその定式化がすごく面倒くさそうだったので、頭の中で図形をぐりぐり動かしてつかんだイメージをそのまま文字にするやり方で迫ってみたいと思います。なお、以下の内容は東京大学が発表したものではありません。
最大値の算出
正四面体の各頂点に A,B,C,D と記号を振ります(図1)。
まず最大値を求めましょう。
正四面体の正射影がどんな形をしているかですが、光源方向から見て正四面体の面が１つ、または２つ、または３つ見えてシルエットが三角形の場合と、面が2つ見えてシルエットが四角形の2パターンがあります。
最初のシルエットが三角形のパターンのうち、面が２つまたは3つ見えるケースは四面体を「裏返す」と面が１つ見えている場合と同じです。
このパターンで正射影の面積が最大になるのは明らかに、こちらに向いている面の重心の直上方向から見た場合で、その面積は1辺の長さが１の正三角形の面積 \displaystyle\frac{ \sqrt{3}}4 です。
次にシルエットが四角形のパターンです。
正四面体の各頂点 A,B,C,D の平面 α への正射影をそれぞれ、 A’,B’,C’,D’ とします(図2)。
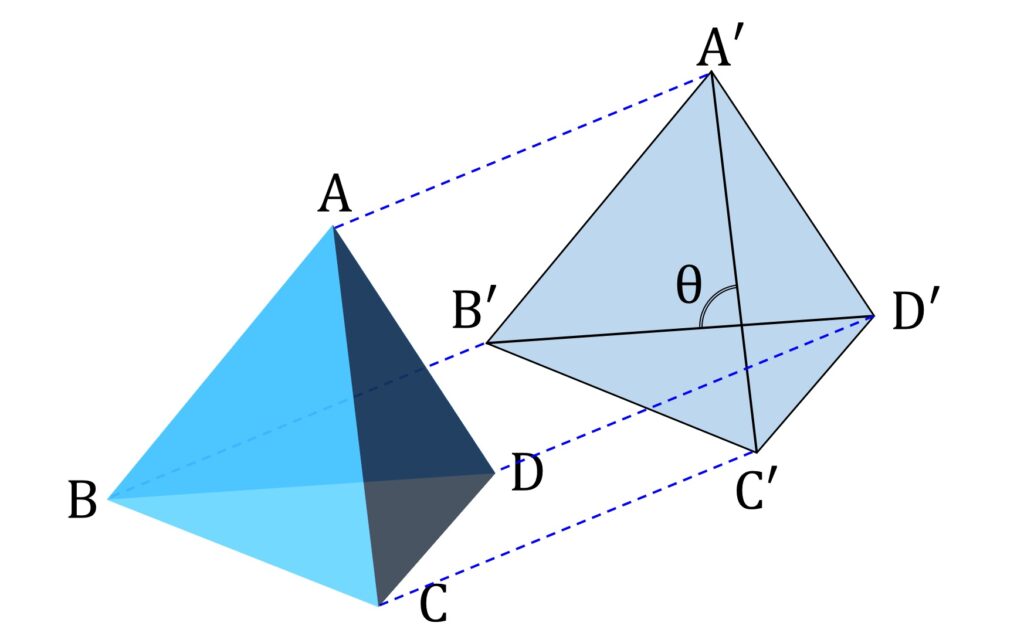
すると線分 A’C’ , B’D’ はそれぞれ AC , BD の正射影であり、 AC = BD = 1 であることから
\begin{aligned}
\mathrm{A'C'} \leqq 1 \\
\mathrm{B'D'} \leqq 1 \\
\end{aligned}です。
よって A’C’ と B’D’ の成す角を θ と置くと、四角形 A’B’C’D’ の面積 S は
S = \frac{1}2 \mathrm{A'C'} \cdot \mathrm{B'D'} \sin \theta \leqq \frac{1}2と評価できます。
ところが、 AC の中点と BD の中点を結ぶ直線 l 上から正四面体 V を見てみる、すなわち直線 l が平面 α に垂直になるように V を配置すると、 A’C’ = B’D’ = 1 かつ A’C’ ⊥ B’D’ なのでV の正射影は正方形であり、
S = \frac{1}2が成り立ちます(図3)。
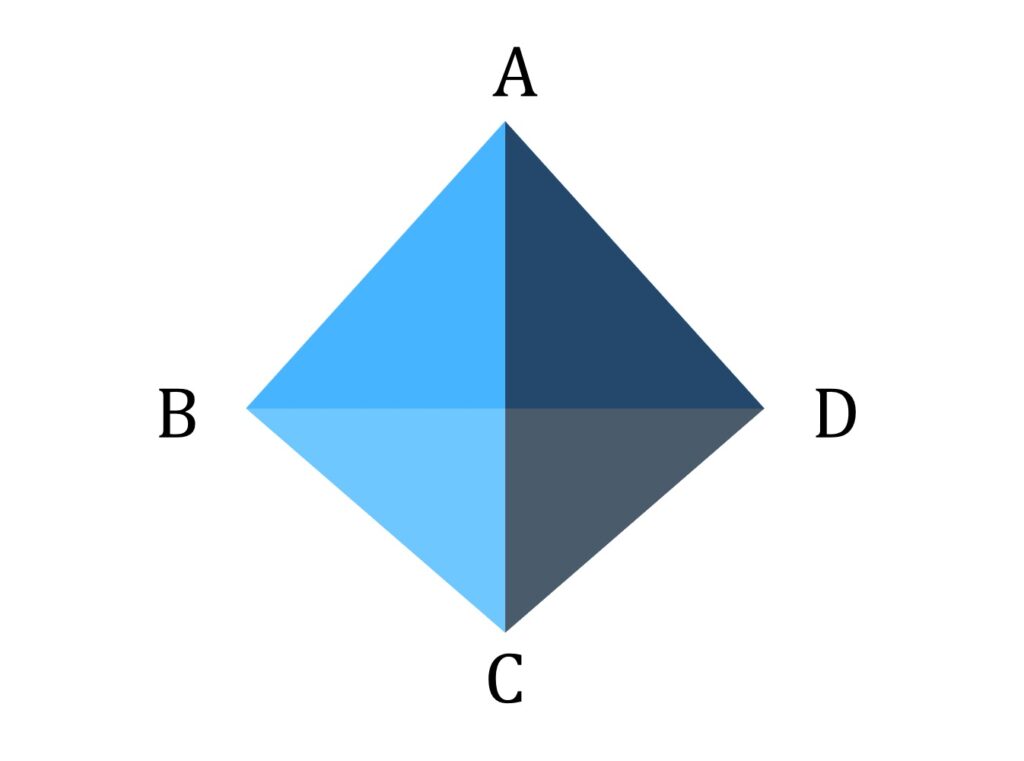
ゆえに S の最大値は \displaystyle\frac{1}2 です。
以上、最大値の方は比較的楽に求めることが出来ました。