最小値の算出
次に S の最小値を求めます。こちらはもう少し大変です。
正射影のシルエットが三角形で、見えている面が1つの場合は、見える面が2つまたは3つの場合と同等です。したがってまず、正射影のシルエットが三角形でかつ、見える面が2つの場合を考察します。
正射影のシルエットが三角形でかつ、見える面が2つの場合
この場合、正四面体 V のどれかの面が平面 α と垂直になっています。そこで面 BCD が α と垂直になっているとします。
このとき、 B’,C’,D’ は同一直線上にあります。 B’D’ を底辺としたときの △A’B’D’ の高さは、 V を面BCD が底面である三角錘 と見立てたときの高さであり、その値は \displaystyle\frac{\sqrt{6}}{3} です(図4)。
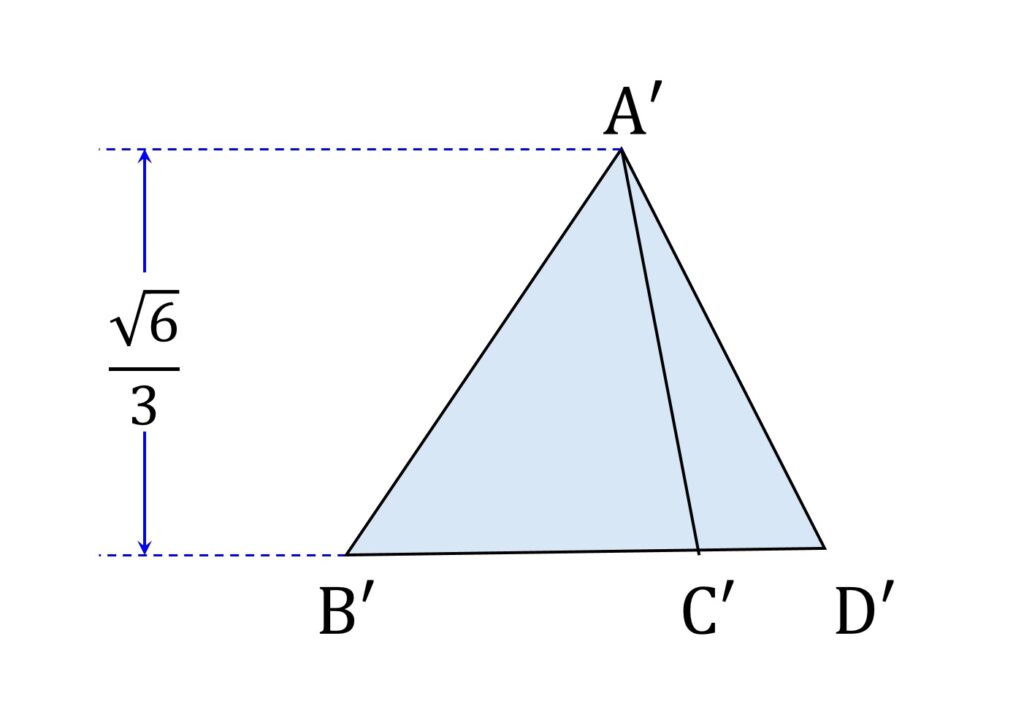
また B’D’ の最小値は明らかに、辺 CD が平面 α と直交するとき(すなわち C’ と D’ が重なるとき)に \displaystyle\frac{ \sqrt{3}}{2} を取ります。
したがって正射影のシルエットが三角形でかつ見える面が2つのとき、正射影の面積 S の最小値は
\frac{\sqrt{3}}{2} \times \frac{\sqrt{6}}{3} \div 2 = \frac{\sqrt{2}}{4}です。
辺 CD が平面 α と直交するということは、面ACD が平面 α と直交するということです。すなわち、正射影のシルエットが三角形でかつ見える面が2つのとき、 S が最小値を取る十分条件は V の面のうち2つが α と直交することです。