正射影の難問を定性的に何とかする – 1988年東大 数学 第2問

2024年9月13日2024年9月19日

正射影のシルエットが三角形でかつ、見える面が3つの場合

　次に正射影のシルエットが三角形でかつ、見える面が3つの場合です。面ABD の「手前」に頂点 C があり、△A’B’D’ の内部に C’ があるとします。

　このとき、正射影の三角形 △A’B’D’ の面積は点 C’ が辺 B’D’ から離れるほど大きくなります。したがってこの場合の正射影の面積は、 V を辺 BD を軸に回転させて C’ が B’D’ 上にあるようにした場合の正射影面積より必ず大きくなります。すなわち、 S は常に「正射影のシルエットが三角形でかつ、見える面が2つの場合」の最小値より大きくなります(図5)。

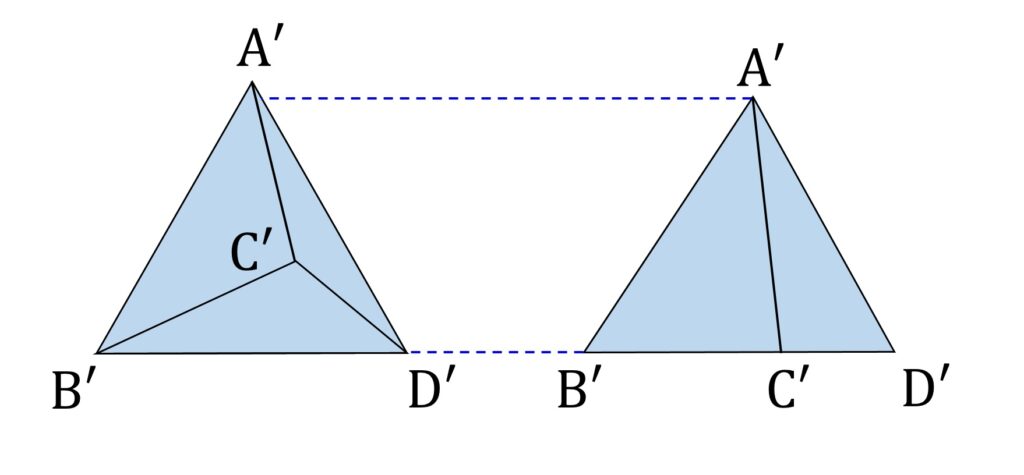
　などと、直感的には明らかなので時間がないときは苦し紛れに言い切ってしまうのも手ですが、実は C’ が B’D’ から「離れすぎる」とこれは成り立たなくなるので、もう一工夫必要です。

　 C’ と B’D’ の「距離感」を定性的に表現できる尺度は無いかと考えるうちに、△ ABD の重心 G に気が付ければ吉です。

　G の正射影を G’ と置くとき、　C’ は△A’B’G’ 、△G’B’D 、△A’ G’D’ のいずれかに必ず含まれます（境界上も可）。そこで、 C’ は△G’B’D’ に含まれるとします(図6)。

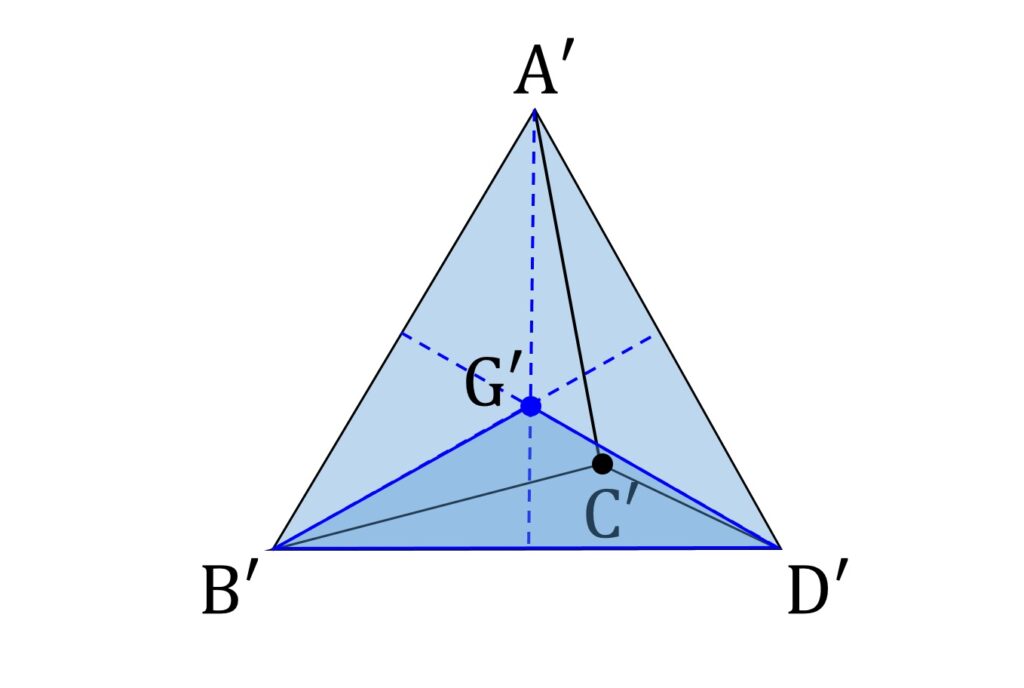
　また、辺 BD を含み、平面 α と垂直な平面を β と置きます。 β と面 BCD の成す角を θ と置きます。 M を BD の中点とします。するとA,C,G,M は同一平面 γ 上に有ります(図7)。

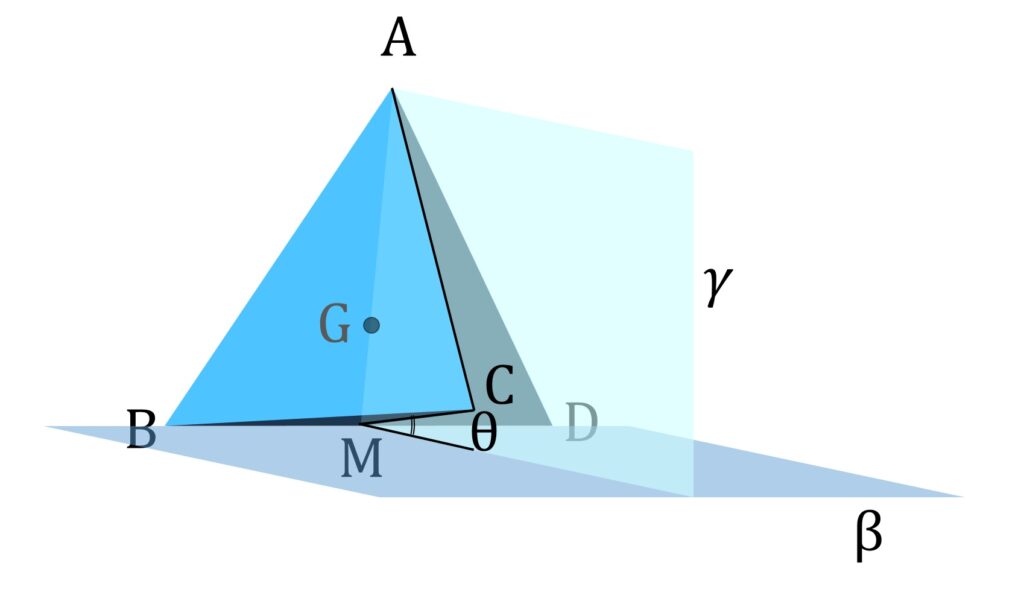
γ は BD を垂直に等分するので BD は γ の法線ベクトルに平行です。 BD は β 上の線分なので β の法線ベクトルと垂直です。よって β の法線ベクトルと γ の法線ベクトルは直交し、 β と γ は直交します。

　ここで、重心 G から平面 β に下ろした垂線の足を H 、頂点 C から平面 β に下ろした垂線の足を I 、それぞれの α への正射影を H’ 、I’ と置きます(図8)。

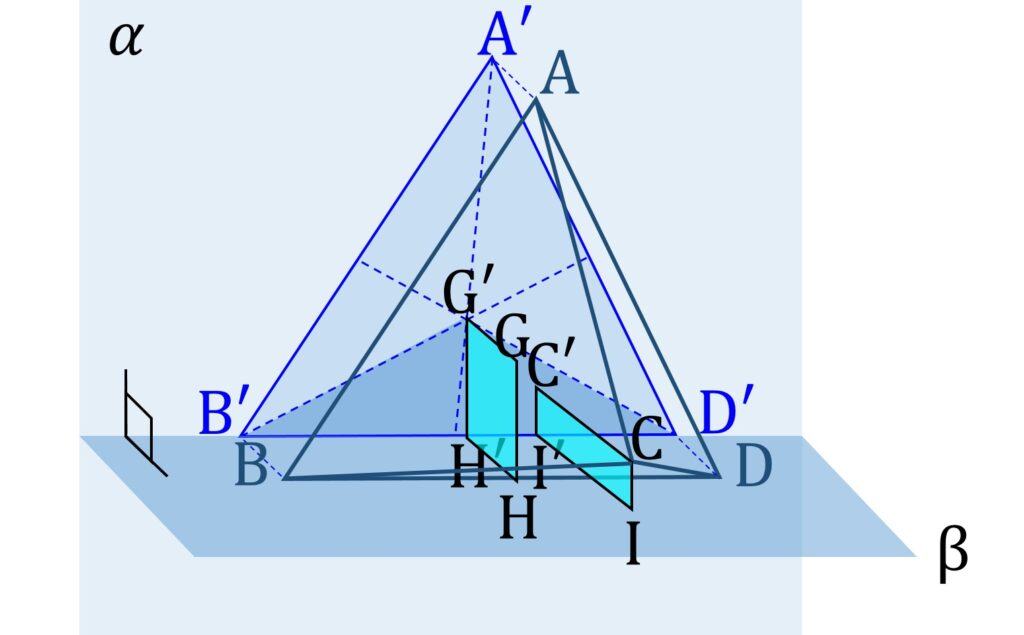
　このとき GH 、 CI は射影面 α と平行なので、明らか GH = G’H’ 、 CI = C’I’ が成り立ちますが、これを詳しく説明すると、まず G,H,G’,H’ は同一平面上にあります。また、正射影の定義から明らかに GG’ ⊥ G’H’ 、 HH’ ⊥ G’H’ です。

　 GH は β と直交するので β の法線ベクトルと平行ですが、 α と β も直交するので GH は α の法線ベクトルと直交します。 GG’ は α の法線ベクトルと平行なので GH ⊥ GG’ が成り立ちます。

　四角形 GHH’G’ の4つの角のうち3つまでが直角なので四角形 GHH’G’ は長方形であり、したがって GH = G’H’ です。同様に CI = C’I’ が成り立ちます。

　 C’ が△G’B’D’ の内部にあるので C’I’ ≦ G’H’ です。したがって CI ≦ GH が成り立ちます。

　G から β に下した垂線の足が H であることと β と γ が直交することから、 H は γ 上の点です。同様に I も γ 上の点です。 γ 上の各点を描画すると図9のようになります。

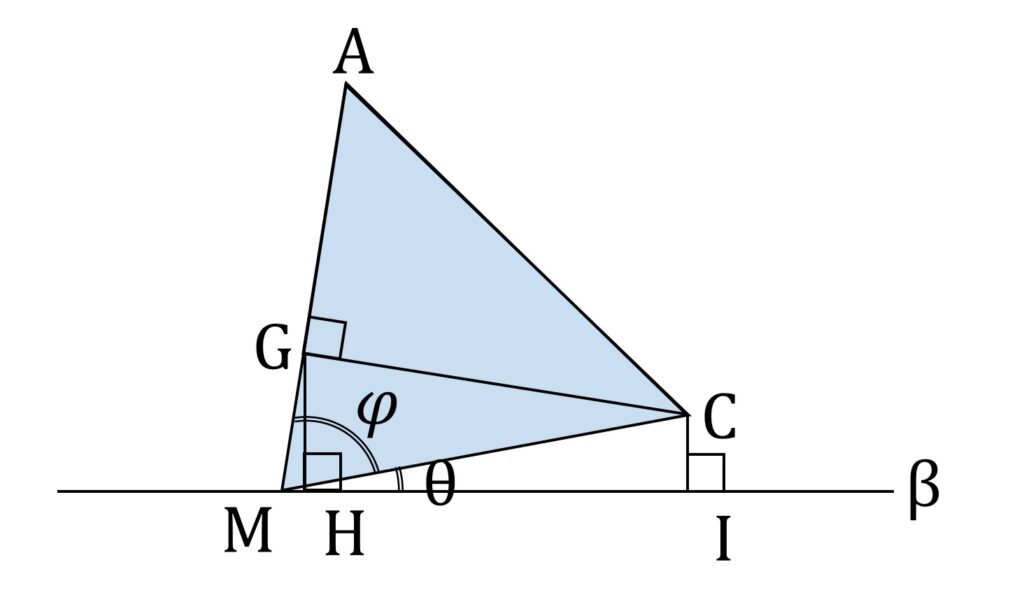
　φ = ∠AMC と置きます。 すると CI ≦ GH であったので

  \angle \mathrm{AMI} = \theta + \varphi \leqq \frac{\pi}{2}

です。 0 \leqq x \leqq \displaystyle\frac{\pi}{2} のとき sin x は単調増加なので、

\sin ( \theta + \varphi ) \geqq \sin \varphi

が成り立ちます。一方、G’ は △A’B’D’ の重心であったので、 △A’B’D’ の B’D’ を底辺としたときの高さ h は G’H’ の3倍です。

　したがって

\begin{aligned} 
 h &= 3\mathrm{G'H'}  \\
 & = 3\mathrm{GH }  \\
 &=  3\mathrm{GM}\sin ( \theta + \varphi)  \\
&=  \mathrm{AM}\sin ( \theta + \varphi)  \\ 
 & \geqq  \mathrm{AM}\sin   \varphi 
\end{aligned}

ですが、

\begin{aligned}
 \mathrm{AM}  & = \frac{\sqrt{3}}{2} \\
 \sin \varphi  &= \frac{2 \sqrt{2}}{3}
\end{aligned}

なので

\begin{aligned} 
  h \geqq  \frac{\sqrt{6}}{3}
\end{aligned}

が成り立ちます。

　したがって

　S = \frac{1}{2} \mathrm{B'D'}  \cdot h \geqq  \frac{\sqrt{6}}{6} \mathrm{B'D'}

　ですが、正射影のシルエットが三角形でかつ、見える面が2つの場合で確認したように、

\mathrm{B'D'} \geqq \frac{\sqrt{3}}{2}

なので、

S \geqq \frac{\sqrt{2}}{2}

が成り立ちます。