正射影の難問を定性的に何とかする – 1988年東大 数学 第2問
正射影のシルエットが四角形でかつ、見える面が2つの場合
面 ABC、面 ACD が見えているものとします。平面 ζ を、平面 β と平行でかつ、点 C を通るものとします(図10)。
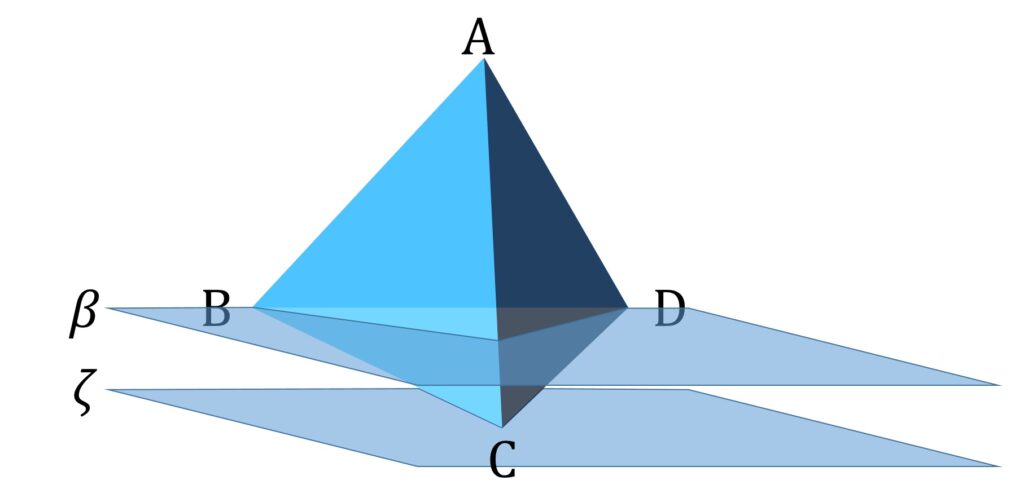
ここで V を辺BD を軸として回転させます。すると A’C’ は辺 AC が α と平行なときに最大になり、 C’ が B’D’上にあるときに最小になります。よって S も C’ が B’D’上にあるときに最小になるような気がします(図11)。
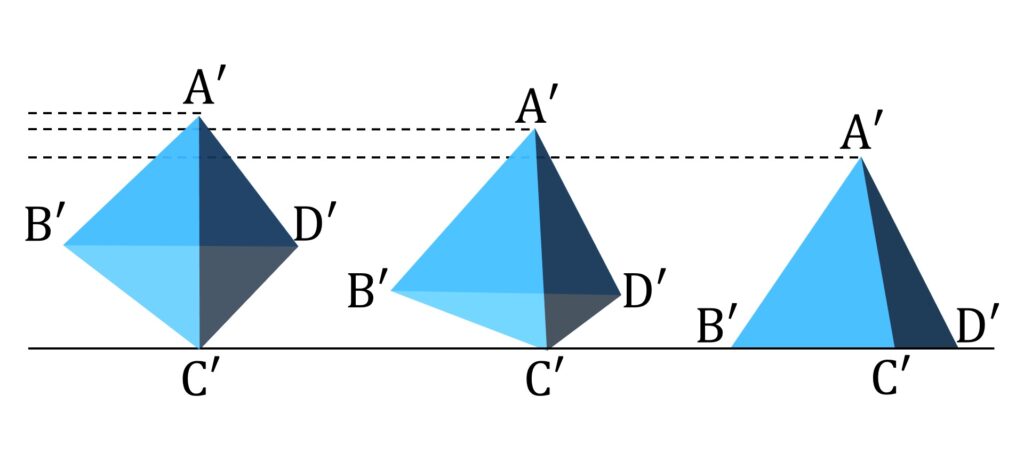
C’ が B’D’上にあるときに面積が一番小さいということは、 S は常に「正射影のシルエットが三角形でかつ、見える面が2つの場合」の最小値より大きくなります。
そこでこれを証明します。
頂点 A から平面 ζ に下ろした垂線の足を H と置き、面BCD と ζ の成す角を θ と置きます。 BD を垂直に等分する平面を γ と置くとき、BD の中点 M および A ,C,H は γ 上にあります(図12)。
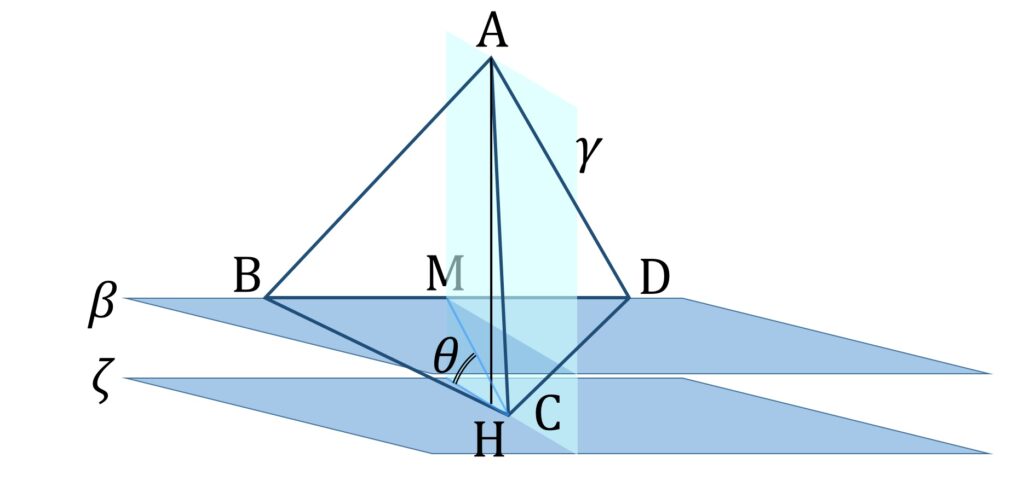
また、H の α への正射影を H’ と置きます。すると ζ と β は平行なので、「正射影のシルエットが三角形でかつ、見える面が3つの場合」と同様に AH = A’H’ および A’H’ ⊥ B’D’ が成り立ちます。よって
S = \frac{1}2 \mathrm{B'D'} \cdot \mathrm{A'H'}が成り立ちます(図13)。
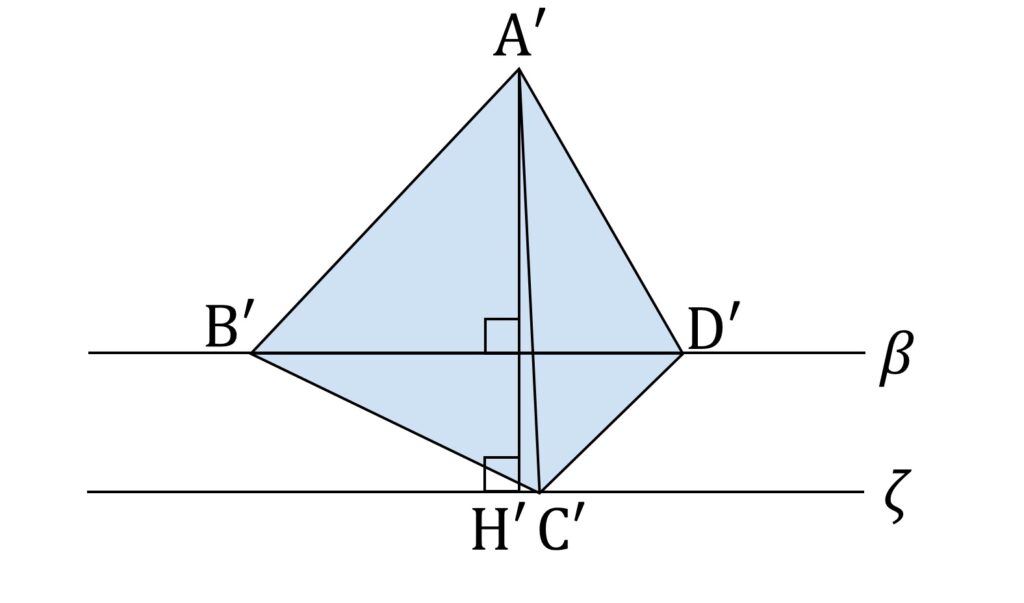
φ = ∠AMC と置き、面 BCD と ζ の成す角を θ と置きます。 γ 上の各点を描画すると図14のようになります。
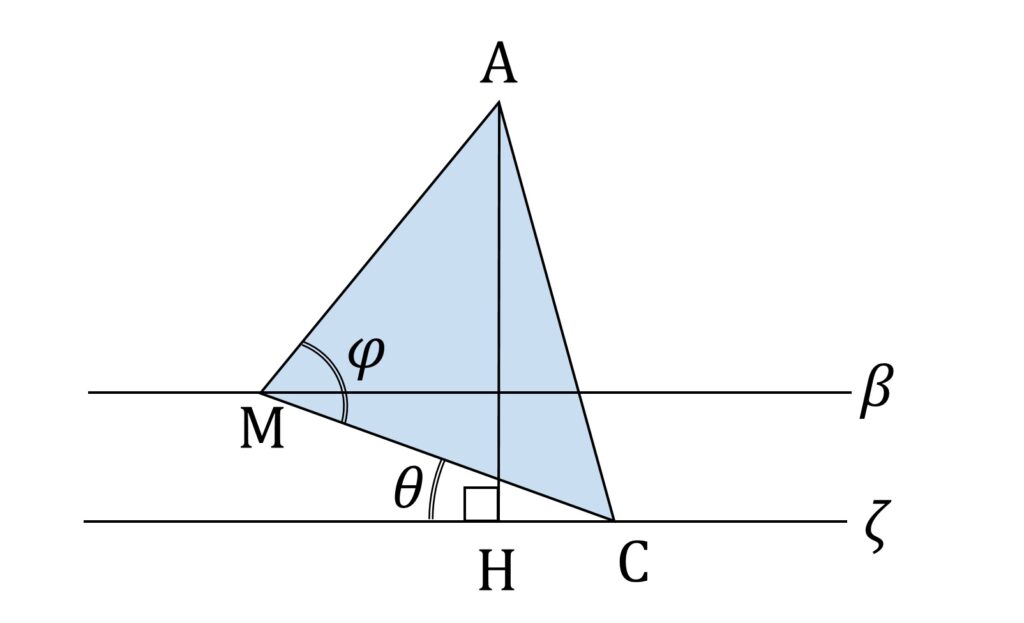
このとき、
\mathrm{AH }= \sin ( \frac{\pi - \varphi}{2} + \theta)が成り立ちます（ AM = CM および AC = 1 に注意）。ここで \theta \leqq \displaystyle\frac{\varphi}{2} であるとして一般性を失いません（もし \theta > \displaystyle\frac{\varphi}{2} なら、「上下をひっくり返して」平面 ζ が A を通るように定義すればよい）。よって
\begin{aligned}
S & = \frac{1}{2}\mathrm{B'D' } \cdot\mathrm{A'H' } \\
& = \frac{1}{2}\mathrm{B'D' } \cdot\mathrm{AH } \\
&=\frac{1}{2}\mathrm{B'D' } \sin ( \frac{\pi - \varphi}{2} + \theta) \\
& \geqq \frac{1}{2} \mathrm{B'D' } \sin ( \frac{\pi - \varphi}{2} ) \\
&= \frac{1}{2} \mathrm{B'D' } \cos \frac{\varphi}{2} \\
&= \frac{1}{2} \mathrm{B'D' } \sqrt{\frac{1 + \cos \varphi}{2}} \\
& = \frac{1}{2} \mathrm{B'D' } \sqrt{\frac{1 + \frac{1}3 }{2}} \\
&= \frac{\sqrt{6}}{6} \mathrm{B'D' } \geqq \frac{ \sqrt{2}}4
\end{aligned}が成り立ちます。
以上、 S は V の面のうち２つが α と直交するとき、最小値 \displaystyle\frac{ \sqrt{2}}{4} を取ります。
解法のポイント
立体図形の問題は図に書くとイメージしやすいので、まずは図を書いて方針を策定しましょう。証明も数式に落とすより図で説明したほうが速いことがあるので、特に時間がないときは本稿のように図と定性的な説明で押し切るのもありでしょう。
また、正四面体や正八面体は変な方向から見ると思いもよらない形に見えるので、普段から確認しておきましょう。