1994年東大 数学 第6問 小問2の解法
「d(O, P) = d(P, Q) となるような a ≧ 0 が存在する」点 P(x, y) の範囲を求めよというのがお題ですが、 P を起点に考えるのは難しそうなので、 a ≧ 0 が与えられたときにd(O, P) = d(P, Q) を満たす P の存在範囲がどうなっているのかを考えてみます。このアプローチだと、小問1のやり方が応用できます。
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = |x| +|y| \\
d( \mathrm{P} ,\mathrm{Q}) &= |x-a| +|y-a^2-1| \\
\end{aligned}なので、これらの絶対値を外すためには小問1のときと同様に、 x,y の双方とも以下のように3つの範囲に分類する必要があります。
\begin{aligned}
&x < 0 \\
&0 \leqq x < a \\
& a \leqq x \\
& y < 0 \\
& 0 \leqq y < a^2 + 1 \\
& a^2 +1 \leqq y \\
\end{aligned}よって場合分けの総数は 3 ☓ 3 = 9 通りです。今回は小問1のような対称性がないので、愚直に全9パターンをさらう必要があります(やれやれ)。
各パターンごとに、d(O, P) = d(P, Q) を満たす P がどのように分布しているかを調べます(図4)。
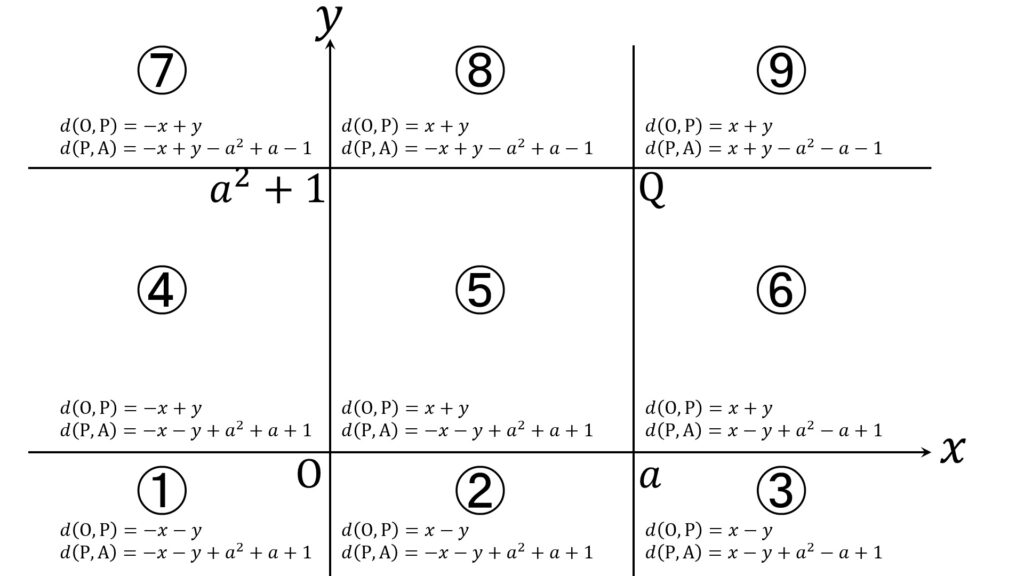
➀ x < 0 かつ y < 0 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = -x -y\\
d( \mathrm{P} ,\mathrm{Q}) &= -x- y +a^2+a+1 \\
\end{aligned}なので、d(O, P) = d(P, Q) を満たす P は存在しません。
② 0 ≦ x < a かつ y < 0 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x -y\\
d( \mathrm{P} ,\mathrm{Q}) &= -x- y +a^2+a+1 \\
\end{aligned}なので、d(O, P) = d(P, Q) を満たす P は直線 x = \displaystyle\frac{a^2 + a + 1}{2} 上に存在しますが、これはエリア外です。
③ a ≦ x かつ y < 0 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x -y\\
d( \mathrm{P} ,\mathrm{Q}) &= x- y +a^2-a+1 \\
\end{aligned}なので、d(O, P) = d(P, Q) を満たす P は存在しません。
④ x < 0 かつ 0 ≦ y < a2+1 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = -x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= -x- y +a^2+a+1 \\
\end{aligned}なので、d(O, P) = d(P, Q) を満たす P は直線 y = \displaystyle\frac{a^2 + a + 1}{2} 上に存在します。
⑤ 0 ≦ x < a かつ 0 ≦ y < a2+1 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= -x- y +a^2+a+1 \\
\end{aligned}なので、d(O, P) = d(P, Q) を満たす P は直線 x + y = \displaystyle\frac{a^2 + a + 1}{2} 上に存在します。
⑥ a ≦ x かつ 0 ≦ y < a2+1 のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= x- y +a^2-a+1 \\
\end{aligned}なので、d(O, P) = d(P, Q) を満たす P は直線 y = \displaystyle\frac{a^2 - a + 1}{2} 上に存在します。
⑦ x < 0 かつ a2+1 ≦ y のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = -x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= -x+ y -a^2+a-1 \\
\end{aligned}なので、d(O, P) = d(P, Q) を満たす P は存在しません。
⑧ 0 ≦ x < a かつ a2+1 ≦ y のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= -x+ y -a^2+a-1 \\
\end{aligned}なので、d(O, P) = d(P, Q) を満たす P は直線 x = -\displaystyle\frac{a^2 - a + 1}{2} 上に存在しますが、これはエリア外です。
⑨ a ≦ x かつ a2+1 ≦ y のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= x+ y -a^2-a-1 \\
\end{aligned}なので、d(O, P) = d(P, Q) を満たす P は存在しません。
以上をまとめると、 a ≧ 0 が与えられたときにd(O, P) = d(P, Q) を満たす P の存在範囲は図5の通りです。
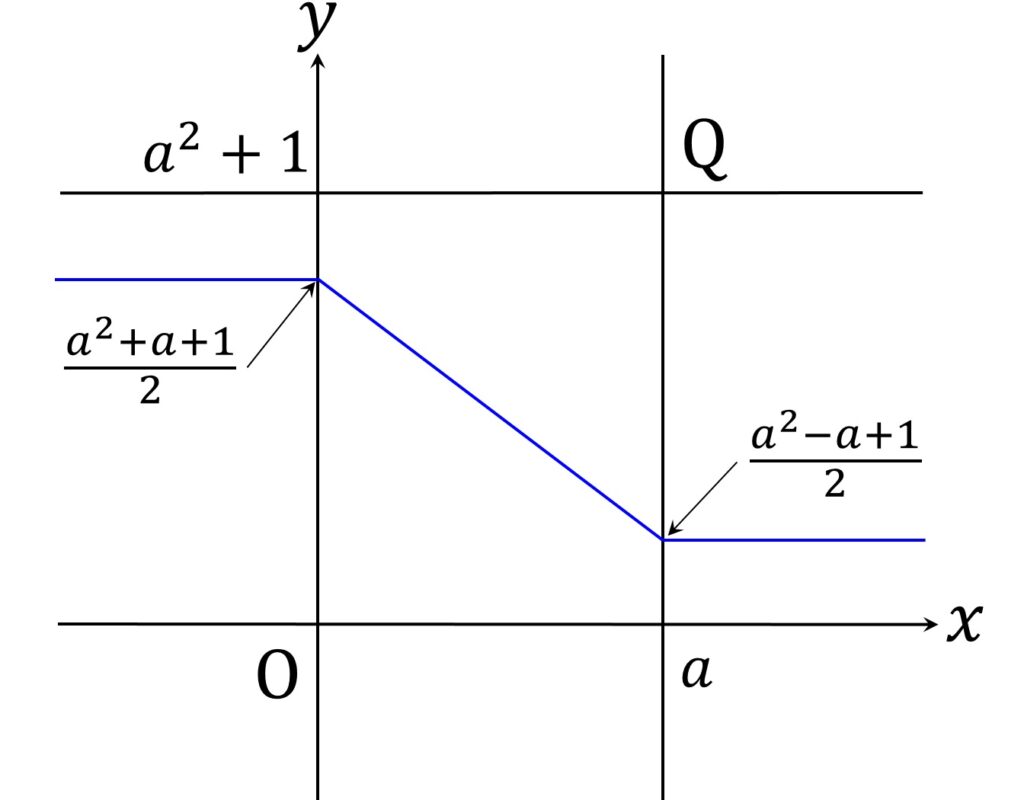
したがって a ≧ 0 が与えられたとき、点 R を \mathrm{R} ( a, \displaystyle\frac{a^2-a +1}{2} ) と定義すると、 R が a の値に応じて曲線 y = \displaystyle\frac{x^2-x +1}{2} 上を動くとき、d(O, P) = d(P, Q) を満たす P が存在する折れ線は図6のエリアを網羅します。
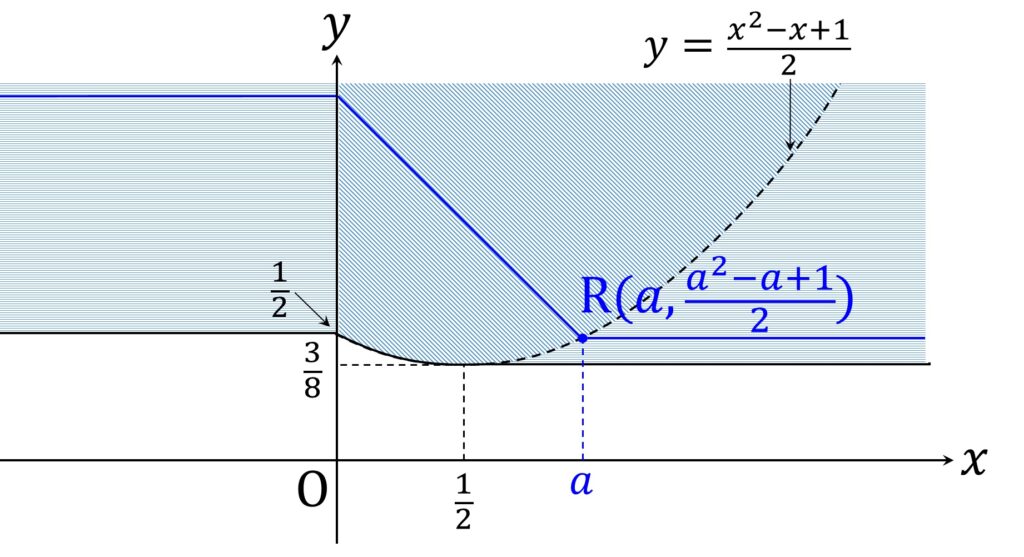
ゆえに条件(*)を満たすPの存在範囲は図6で示したエリア(境界含む)です。
などと、時間がないときはこんな感じでまとめてもよいと思いますが、少しモヤっとするので、原点 O(0, 0) に対し,d(O, P) = d(P, Q) となるような a ≧ 0 が存在するための必要十分条件が P が図6のエリアに存在することであることを、もう少しきちっと示します。