必要性の表明
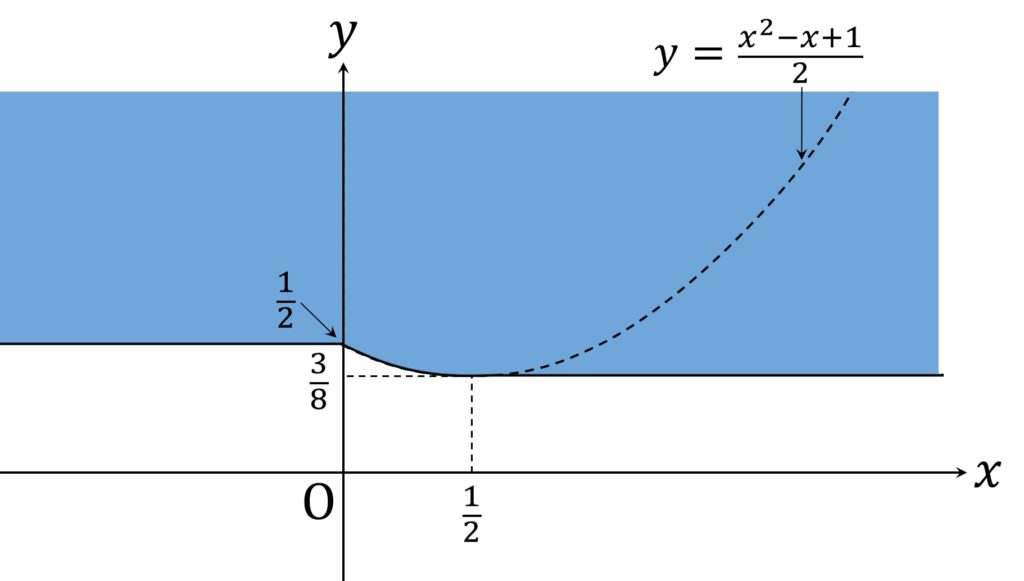
必要条件「 d(O, P) = d(P, Q) となるような a ≧ 0 が存在するならば、 P は図6のエリアに存在する」の対偶は、「P は図6のエリアに存在しないならば、 d(O, P) = d(P, Q) となるような a ≧ 0 は存在しない」なので、これを証明します。
図6のエリア以外を以下の図8のように4つに分割します。
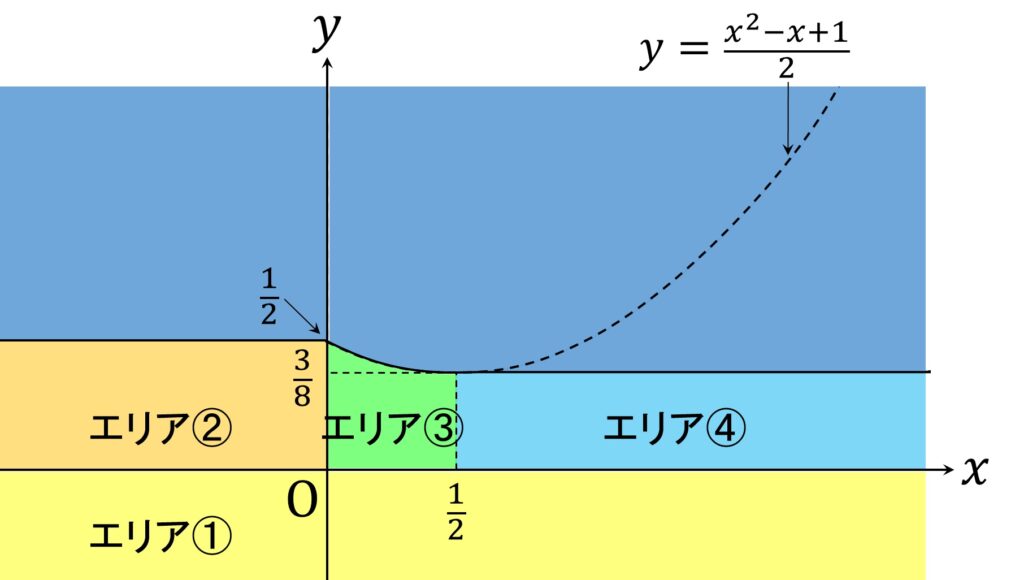
各エリアの定義は以下の通りです。
\begin{aligned}
& \text{エリア➀} : \{(x,y) \in \mathbb{R}^2 | y < 0 \} \\
& \text{エリア②} : \{(x,y) \in \mathbb{R}^2 | x < 0 \text{かつ} 0 \leqq y <\frac{1}2 \} \\
& \text{エリア③} : \\
&\{(x,y) \in \mathbb{R}^2 | 0 \leqq x < \frac{1}2 \text{かつ} \\
& \text{ }0 \leqq y < \frac{x^2-x+1}2 \} \\
& \text{エリア④} : \{(x,y) \in \mathbb{R}^2 | \frac{1}{2} \leqq x \text{かつ} 0 \leqq y < \frac{3}8 \} \\
\end{aligned}P ∈エリア①のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = |x| -y\\
d( \mathrm{P} ,\mathrm{Q}) &= |x-a|+ a^2+1 -y \\
\end{aligned}なので
\begin{aligned}
d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) & = |x-a| -|x|+ a^2+1 \\
\end{aligned}であり、 x < 0 のとき任意の a ≧ 0 に対して
\begin{aligned}
d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) & = a-x+x+ a^2+1 \\
& = a^2+a+1 > 0
\end{aligned}です。
一方 0 ≦ x のとき、 x < a である a に対して
\begin{aligned}
d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) & = a-x -x+ a^2+1 \\
& = a^2+a+1 -2x \\
& > a^2+a+1 -2a \\
& = a^2-a+1 > 0
\end{aligned}a ≦ x である a に対して
\begin{aligned}
d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) & = x- a -x+ a^2+1 \\
& = a^2-a+1 > 0
\end{aligned}であり、 d(O, P) = d(P, Q) となるような a ≧ 0 は存在しません。
P ∈エリア②のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = -x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= a-x+ a^2+1 -y \\
\end{aligned}なので任意の a ≧ 0 に対して
\begin{aligned}
d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) & = a^2+a+1 -2y \\
&> a^2+a \geqq 0
\end{aligned}であり、 d(O, P) = d(P, Q) となるような a ≧ 0 は存在しません。
P ∈エリア③のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= |x-a|+ a^2+1 -y \\
\end{aligned}なので
\begin{aligned}
& d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) \\
& = |x-a| + a^2+1 -x -2y \\
\end{aligned}であり、 x < a である a に対して
\begin{aligned}
&d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) \\
& = a-x + a^2+1 -x -2y \\
& = a^2+a+1 -2x-2y \\
& > a^2+a+1 -2x -x^2+x-1 \\
& = a^2 - x^2 +a-x \\
& = (a-x)(a+x+1) >0
\end{aligned}です。
また、 x ≧ a である a に対して
\begin{aligned}
& d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) \\
& = x-a + a^2+1 -x -2y \\
& = a^2-a+1 -2y \\
& > a^2-a+1 -x^2+x-1 \\
& = a^2 - x^2 -a+x \\
& = (a-x)(a+x-1)
\end{aligned}ですが、 a \leqq x < \displaystyle\frac{1}2 なので a+x-1 < 0 であり、したがって
\begin{aligned}
d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) > 0
\end{aligned}です。
P ∈エリア④のとき
\begin{aligned}
d( \mathrm{O}, \mathrm{P} ) & = x +y\\
d( \mathrm{P} ,\mathrm{Q}) &= |x-a|+ a^2+1 -y \\
\end{aligned}なので
\begin{aligned}
d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) & = |x-a| + a^2+1 -x -2y \\
& > |x-a| + a^2+\frac{1}4 -x
\end{aligned}であり、 x < a である a に対して
\begin{aligned}
d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) & > a-x + a^2+\frac{1}4 -x \\
& = a^2 +a+\frac{1}4 -2x \\
& > a^2 +a+\frac{1}4 -2a \\
& = (a- \frac{1}2)^2 \geqq0
\end{aligned}です。
また、 x ≧ a である a に対して
\begin{aligned}
d( \mathrm{P} ,\mathrm{Q}) -d( \mathrm{O}, \mathrm{P} ) & > x -a + a^2+\frac{1}4 -x \\
& = a^2 -a+\frac{1}4 \\
& = (a- \frac{1}2)^2 \geqq0
\end{aligned}です。
ゆえにP は図6のエリアに存在しないならば、 d(O, P) = d(P, Q) となるような a ≧ 0 は存在しないことが証明できました。
以上、問題文の条件 (*) が成り立つ必要十分条件は点 P が図6の領域に存在することであり、それを改めて描画すると図9のとおりです(境界含む)。