魔の絶対値地獄難問 – 1994年東大数学第6問

符号反転パターンの組み合わせが大変（wal_172619によるPixabayからの画像）

2024年10月4日2024年10月17日

うんちく- L1ノルムについて

　ノルムとはざっくり言うと、ベクトルの長さです。ベクトル $\overrightarrow{x} = (x,y )$ に対し、L1ノルムというのは本問に登場してきたように

|| \overrightarrow{x}||_1 = |x| + |y|

で定義されます。これに対し、ベクトルの「普通の」長さをL2ノルムと呼びます。

|| \overrightarrow{x}||_2= \sqrt{|x|^2 + |y|^2}

です。これらは3次元でも同様に定義されます。

　L1ノルムは別名「マンハッタン距離」などと呼ばれることがあります。碁盤目状の市街地を移動するイメージからこのように呼ばれているようですが、日本ならさしずめ「平安京距離」とか「条里制距離」といったところでしょうか。ここまで書いたところで、昔「平安京エイリアン」というゲームがあったのを思い出しました（何もかもみな懐かしい）。

　L1ノルムとL2ノルムのそれぞれが1になるベクトルの先端の集合を図示すると、図10のようになります。

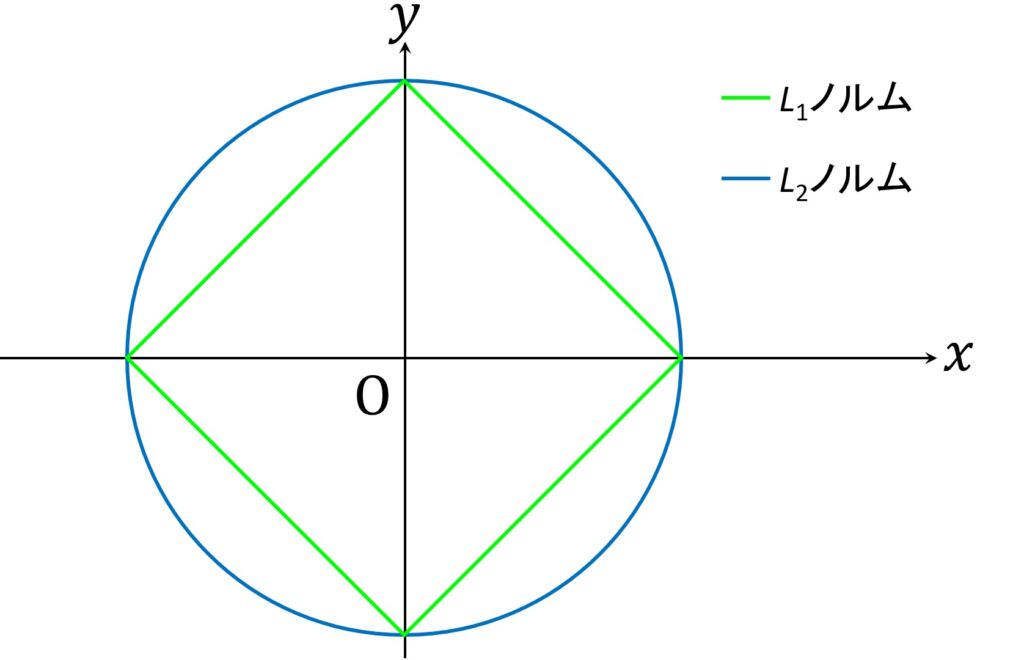
　L2のほうは当然円になりますが、L1のほうはダイヤ型になります。まあ、一次式で定義されているので当然ですが。また一般に

|| \overrightarrow{x}||_2 \leqq || \overrightarrow{x}||_1

が成り立ちます。まあこれも、L1のほうが「遠回り」なので当然といえば当然ですが。

　L1ノルムは本問のように受験生をハメるためだけにあるわけではなく、昨今では機械学習の評価関数にも使われています。機械学習というのはざっくり言うと、評価関数（出力結果と正解との誤差みたいなものだとイメージしてください）が0に近づくようにパラメータを調整するのですが、L2ノルムより「でかい」ため、より早く学習が進む場合があります。