2018年東大 数学 第5問 小問2の解法
多分小問1の絶対値評価から軌跡の方程式が得られるのでしょう。条件が絶対値ということから、軌跡はきっと円とか楕円とかの二次曲線であることが予想できます。
そうなると、 w を複素数のまま引っ張っていくのはつらそうなので、やや原始的ながら
w = x +yi(x,y \text{は実数} )と置いて、 x,y の式に帰着させることにします。
ところが
x = \frac{z + \overline{z}}2なので、
\begin{aligned}
\frac{ | w + \overline{w} -1| }{|w| } & = \left |\frac{ 2x -1 }{ \sqrt{x^2 +y^2} } \right|=2
\end{aligned}であり、両辺を2乗して分母を払うと
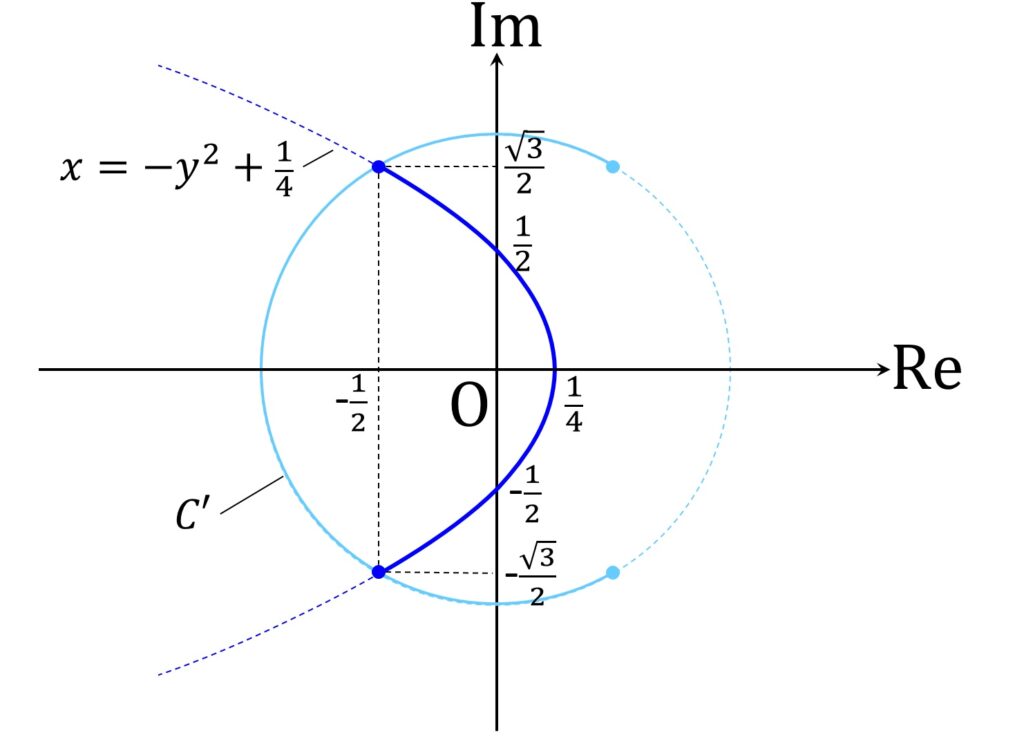
x = -y^2 + \frac{1}4を得ます。予想通り軌跡は二次曲線(放物線)でした!
あとは軌跡の範囲を求めるだけです。
こういう複素数二次曲線系の存在範囲の問題は、複素数の偏角を利用するとスッキリ解けることが多いので、まずはその方向で考えます。
z の偏角を θ 、 w の偏角を φ と置きます。すると問題文の条件より
\frac{\pi}{3} \leqq \theta \leqq \frac{5\pi}{3}ですが、 φ と θ の関係性を見つけられれば答えに手が届きます。
ところが
w = \frac{1}{1-u} = - \frac{1}{tz} = - \frac{\overline{z}}{t}であることと、共役複素数は複素数平面上の実軸に関して元の複素数の対称位置にあるので、その偏角は元の複素数の偏角の符号を反転させたものなので、
\arg( \overline{z}) = -\arg(z) =-\thetaです。
また、 -複素数は複素数平面上の原点に関してもとの複素数と対称の位置にあるので、その偏角はもとの複素数の偏角に π を足したものに等しく、
\arg(- \overline{z}) = \arg( \overline{z}) + \piです。
さらに、 \displaystyle\frac{\pi}{3} \leqq \theta \leqq \displaystyle\frac{5\pi}{3} なので
t = 2-z-\overline{z} = 2 -2\cos \theta > 0であり、複素数に正の実数をかけても偏角は変わらないので
\arg (-\frac{\overline{z} }{t}) = \arg( -\overline{z} )です。
したがって
\begin{aligned}
\varphi & = \arg (w) \\
&= \arg(- \frac{\overline{z}}{t}) \\
& = \arg(- \overline{z}) \\
&=\arg( \overline{z}) + \pi \\
&= -\theta + \pi
\end{aligned}であり、 \displaystyle\frac{\pi}{3} \leqq \theta \leqq \displaystyle\frac{5\pi}{3} であったので
- \frac{2 \pi}3 \leqq \varphi \leqq \frac{2 \pi}3です。よって軌跡の範囲は以下の図1のとおりです(端点含む)。