発展 – 二次曲線の極座標表示
複素数の極形式表示は二次元ベクトルの極座標表示と本質的に同じなので、これを押さえておくと本問のような、複素数平面で二次曲線を書いてみよう的な問題で重宝します。
二次曲線の極座標表示は一般に以下のとおりです。
r = \frac{l}{1 + \epsilon \cos \theta}ここに l > 0 および ε ≧ 0 は定数で、 ε を離心率と呼びます。
ε=0 のとき、曲線は円になります。 0 < ε < 1 のときは楕円、 ε = 1 のときは放物線、1 < ε のときは双曲線になります。
本問の場合、 l = \frac{1}2, \epsilon = 1, になっていて、
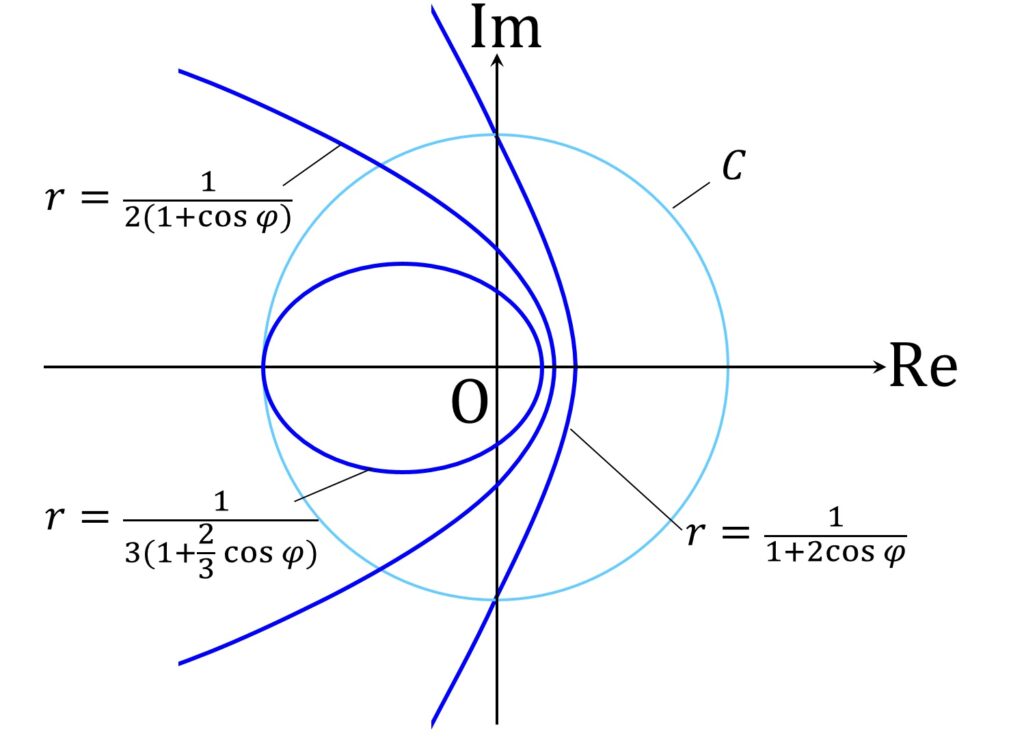
r =|w|= \frac{1}{2(1 + \cos \varphi )}です。
u=2z–z2 でしたが、もしこれが u=3z–z2 であったとすると、
\begin{aligned}
\frac{ | w + \overline{w} -1| }{|w| } & = \left |\frac{ w + \overline{w} -1 }{w } \right| \\
& = \left | 1 + \frac{\overline{w}}{w} -\frac{1}w \right | \\
& = |1 +z^2 -1 +u | \\
& = |z^2 +3z -z^2| \\
& =|3z| =3
\end{aligned}すなわち
|2r \cos \varphi-1| = 3r
であり、
r = \frac{1}{3(1 + \frac{2}3\cos \varphi )}なので、曲線は楕円であることがソッコーわかります。
また u=z–z2 であったとすると、
\begin{aligned}
\frac{ | w + \overline{w} -1| }{|w| } & = \left |\frac{ w + \overline{w} -1 }{w } \right| \\
& = \left | 1 + \frac{\overline{w}}{w} -\frac{1}w \right | \\
& = |1 +z^2 -1 +u | \\
& = |z^2 +z -z^2| \\
& =|z| =1
\end{aligned}すなわち
|2r \cos \varphi-1| = r
であり、
r = \frac{1}{1 + 2\cos \varphi }なので、曲線は双曲線であることがやはりソッコーわかります(図2)。
解法のポイント

本問のように、複素数をベクトルに見立ててその幾何学的な性質を問う問題の場合は、複素数の演算とベクトル演算の関係を理解しておくことが必須です。特に平行とか直交が複素数の演算としてどう表現されるのか、押さえておくようにしましょう。
また、複素数の極形式はべき乗演算や本問のような二次曲線軌跡問題で強みを発揮しますが、この機会に二次曲線の極座標表示を覚えておくと、何かと役に立つでしょう。