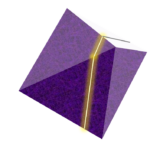
今回取り上げる問題は、 1990年東大 数学 第3問 です。内容は、以下の通りです。

を1辺が1の正八面体、すなわち 空間において、

を満たす点 の集合と合同な立体とする。

(1) の一つの ...

　今回取り上げる、 1995年京大 後期 文系 数学 第4問 は、自分で得点を指定できるという、キャッチーな問題です。とはいってもふざけているわけではなく、実態は剰余類に関する問題です。

　問題文は以下の通りです。 ...

　今回は、3元連立方程式の問題を取り上げます。只の連立方程式ではありません。2次方程式で、しかも変数が循環しています。これは、 1997年京大 後期 数学 第4問 (理系)です。

1997年京大 後期 数学 第4問 とは

　 ...

　数学の大学入試問題で、史上最強と言われているのが、 1998年東大 数学 後期 第3問 です。難しすぎて試験当日に、予備校が解答速報を出すことが出来なかった、という逸話が残るほどの超難問です。今日に至るまで、その隔絶した難しさに迫る ...