今回取り上げる問題は、 1990年東大 数学 第3問 です。内容は、以下の通りです。
V を1辺が1の正八面体、すなわち xyz 空間において、
|x|+|y|+|z| \leqq 1 / \sqrt{ 2 }
を満たす点 (x,y,z) の集合と合同な立体とする。
(1) V の一つの面と平行な平面で V を切ったときの切り口の長さは一定であることを示せ。
(2) 1辺の長さが1の正方形の穴が開いた平面がある。 V をこの平面に触れることなく穴を通過させることが出来るか。結論と理由を述べよ。
東大は正八面体の問題が割と好きなようで、時々出題されます。何等かのこだわりがあるのか、ちょっと不思議な気がします。
8面体は普段あまりなじみのある図形ではありません。思いつくものは、ダイヤモンドの原石くらいです(あと、ヤシマ作戦のアレとか。でも1990年は、初回放映より前です)。
そういった、イメージしにくい図形を扱う本問。一見したところ、空間座標と方程式を使う系統の問題に見えます。
しかし、図形を空間座標で扱うのは、計算が膨大になりがちです。なんか嫌げな感じなので、今回はよりアナログなアプローチでいきます。
小問1の解法
そもそも、 V が正八面体だというところが、あまり自明ではないと思いますが、そこは問題文を信用します。
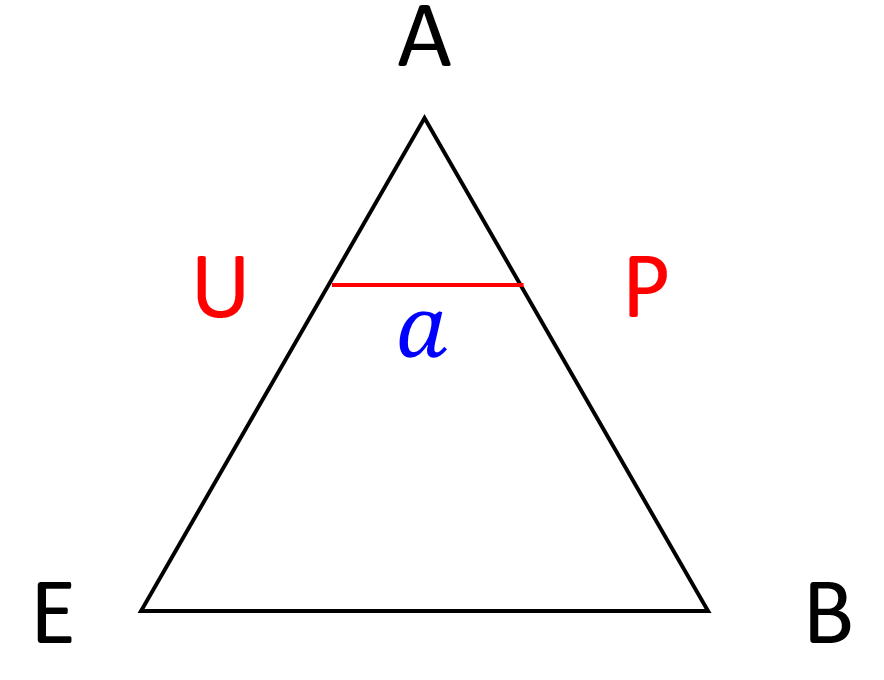
数式はちょっと脇に置いて、問題文の図形的な意味を把握します。正8面体 V に、図1のように頂点記号を付与し、 \triangle{ \mathrm{ACD} } に平行な面で切断したとします。
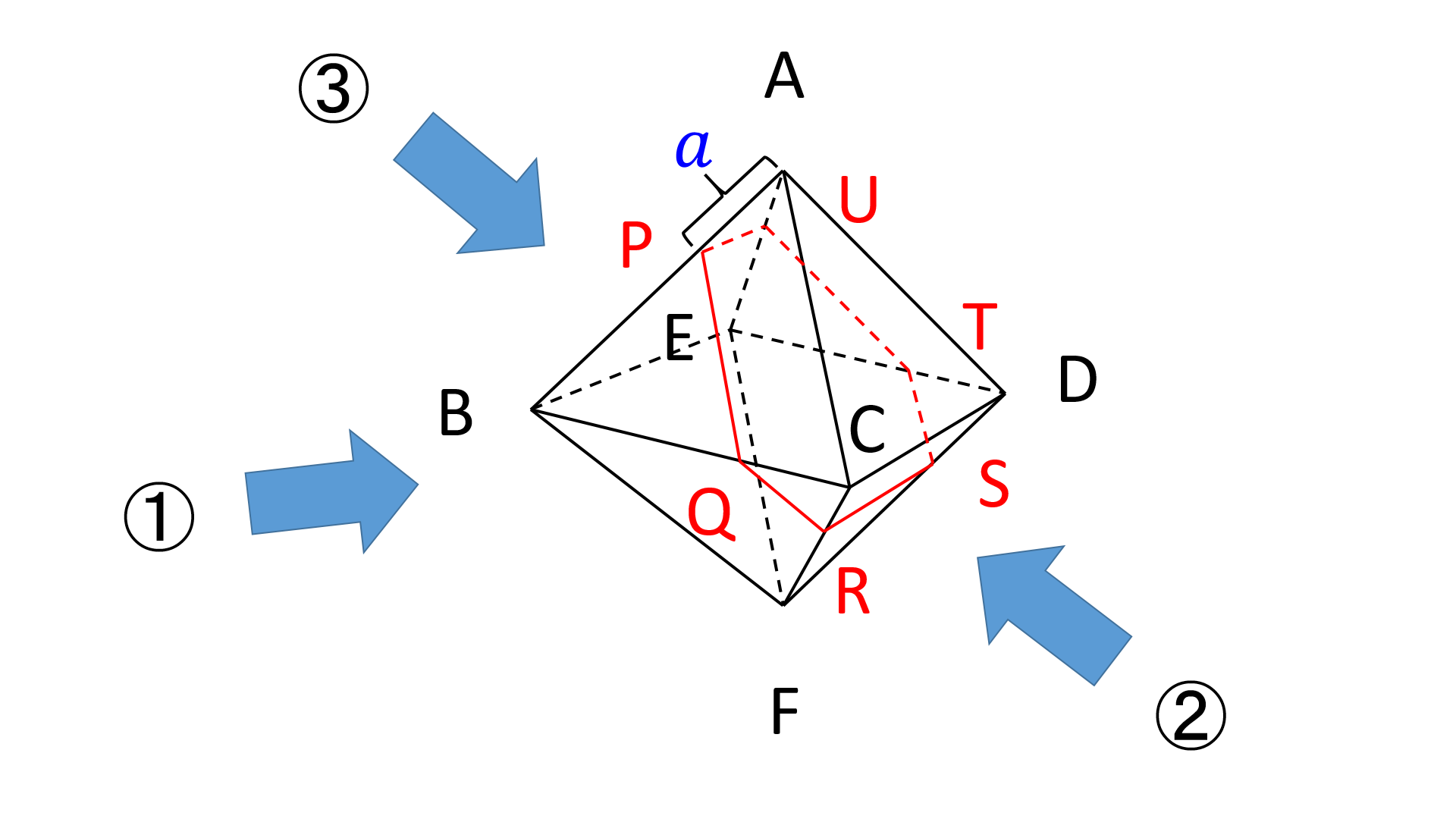
切断面の頂点にそれぞれ、 \mathrm{P} 、 \mathrm{ Q} 、 \mathrm{ R} 、 \mathrm{ S } 、 \mathrm{ T} 、 \mathrm{ U} と記号を付与したとき、図1の横方向(①)から V を見た図が図2、 \triangle{ \mathrm{CDF} } 方向(②)から見た図が図3、 \triangle{ \mathrm{ABE} } 方向(③)から見た図が図4です。 \mathrm{AP} の長さが a \text{ } (0 \leqq a \leqq 1) であるとします。
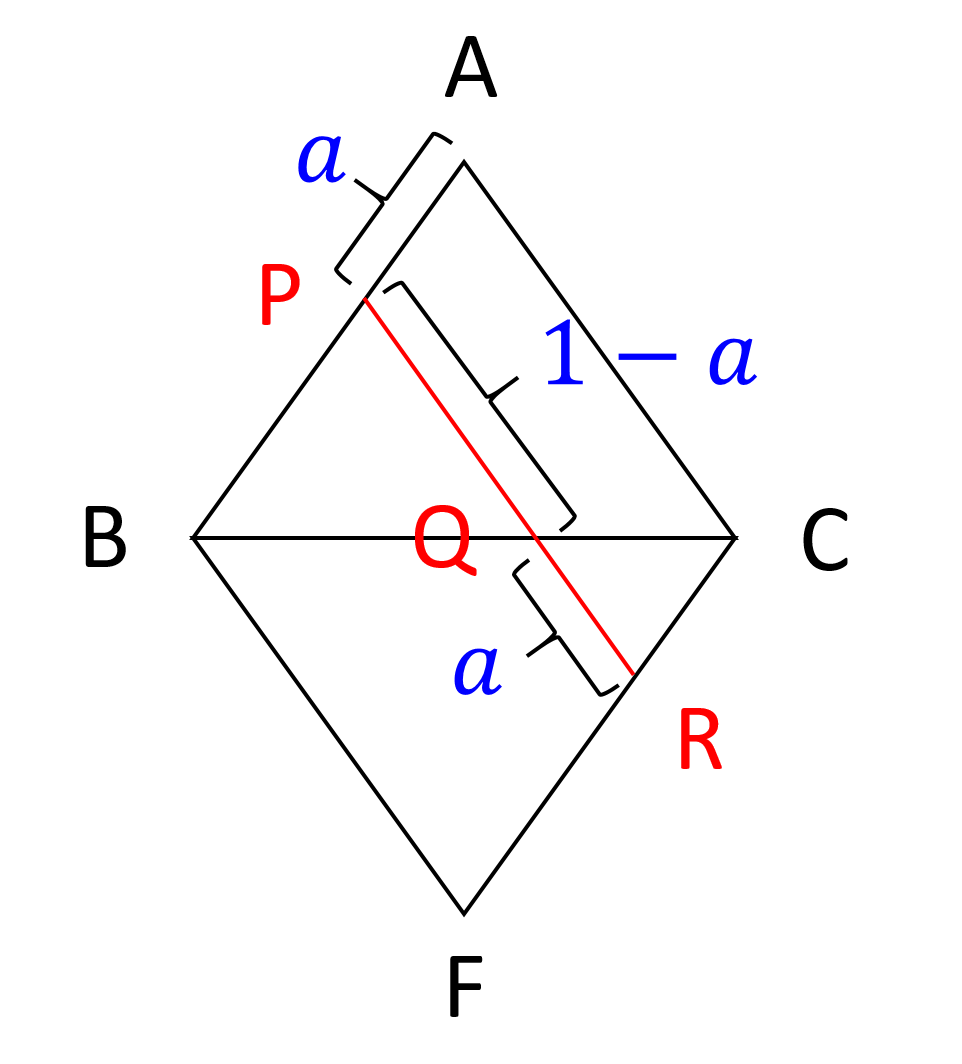
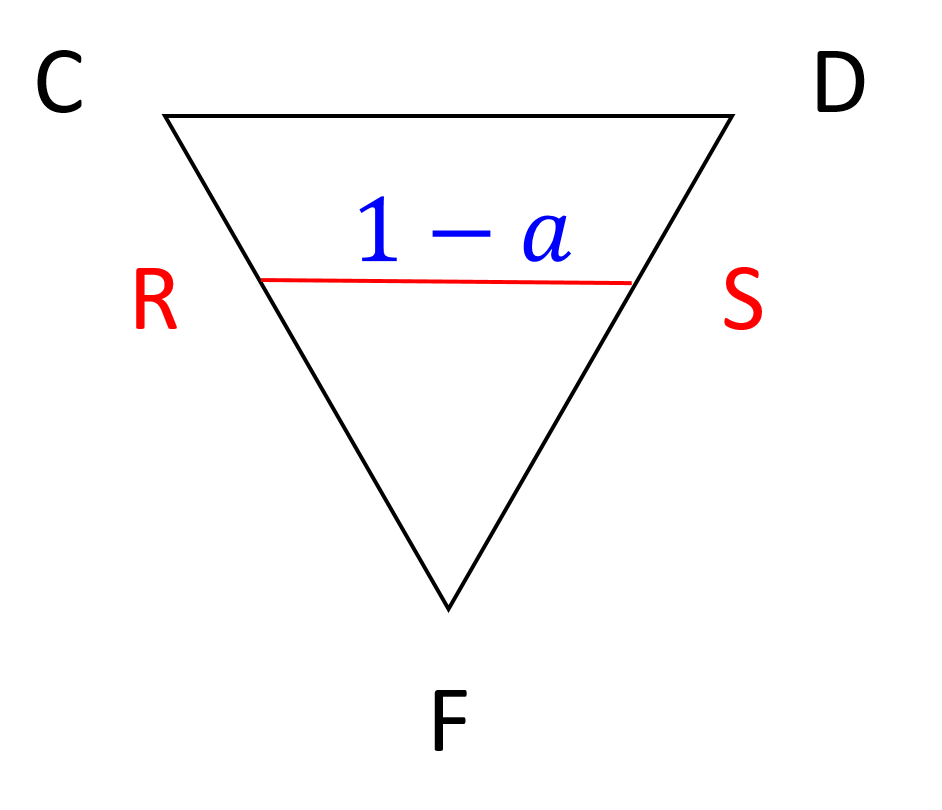
このとき、切断面の形は図5のようになります。周の合計は常に3になるので、題意が証明できたことになります。
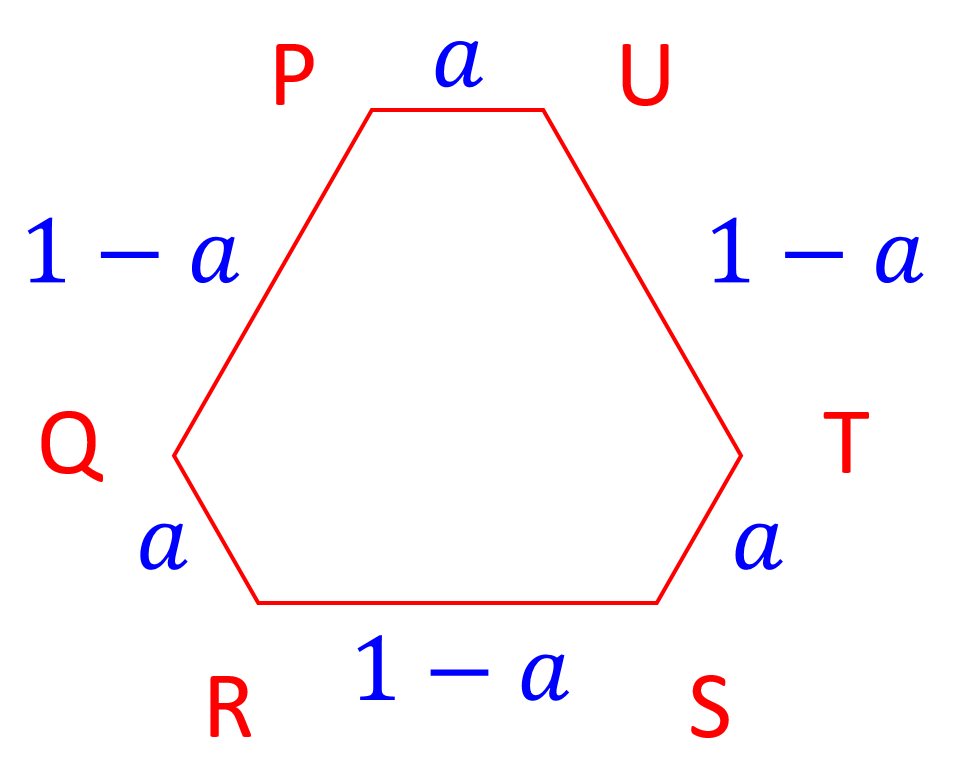
切断面の形が図5になるということは、わざわざ証明しなくても大丈夫だと思います。切断面の各辺の長さが、 \triangle{ACD} に平行だという条件から、 a か 1-a のどちらかであることを示せば、十分でしょう。
図1 が先にあれば、どうと言うことありません。本問は、図1 がイメージできるかどうかがすべてです。
正8面体の切断面なんて、普通は全然イメージできないと思います。そこで、題意に沿って図2から図4までを自分で描いてみます。
切断面が正8面体の各面のどこを通っているのかを描いたうえで、それを正8面体の立体図にプロットすれば、図1の出来上がりです。
とまあ、理屈はそうなのですが、これが今一つしっくりこない場合は、正8面体を上下の2つに分けるアプローチがお薦めです。
正8面体の上半分を描いたのが、図6です。四角錘だと大分、人知の扱える範囲に近づいてきました。切断面が等脚台形なのも、直感的に明らかです。
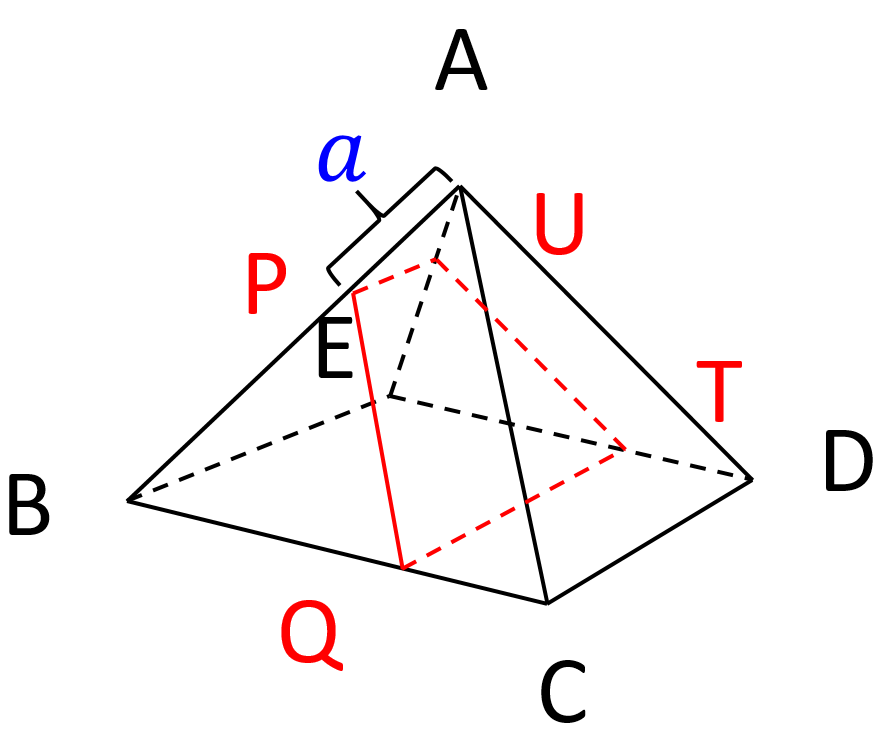
これと、下半分の断面の等脚台形を接合させれば、図5が得られます。ここから逆に図1を作成すれば、今度こそ題意のイメージを完全に把握できることでしょう。
小問2の解法
正8面体 V が、四角い穴を通り抜けられるか、と言う問題です。こういう聞かれ方をするときは、大抵答えはyesなので、まずはその方向で考えます。
小問1で、 V の断面図を苦労して作りましたが、これが1辺の長さが1の正方形の中に常に収まれば、穴を通り抜けられることになります。
そこで図5を改めて見ると、 a の値に関わらず、横幅が1、高さが \frac{ \sqrt{3} }{2} です(図7)。
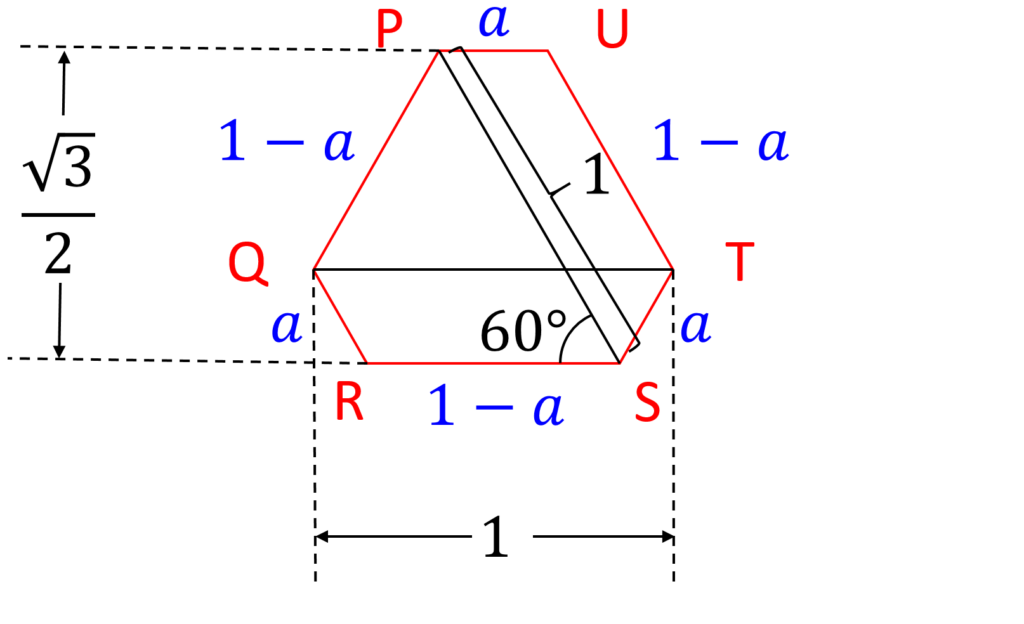
断面を少し傾ければ、余裕で四角い穴を通り抜けられそうです。形状とサイズから、明らかに通り抜けられると言い切って良い気もしますが、もう少し数学っぽい解答にするなら、
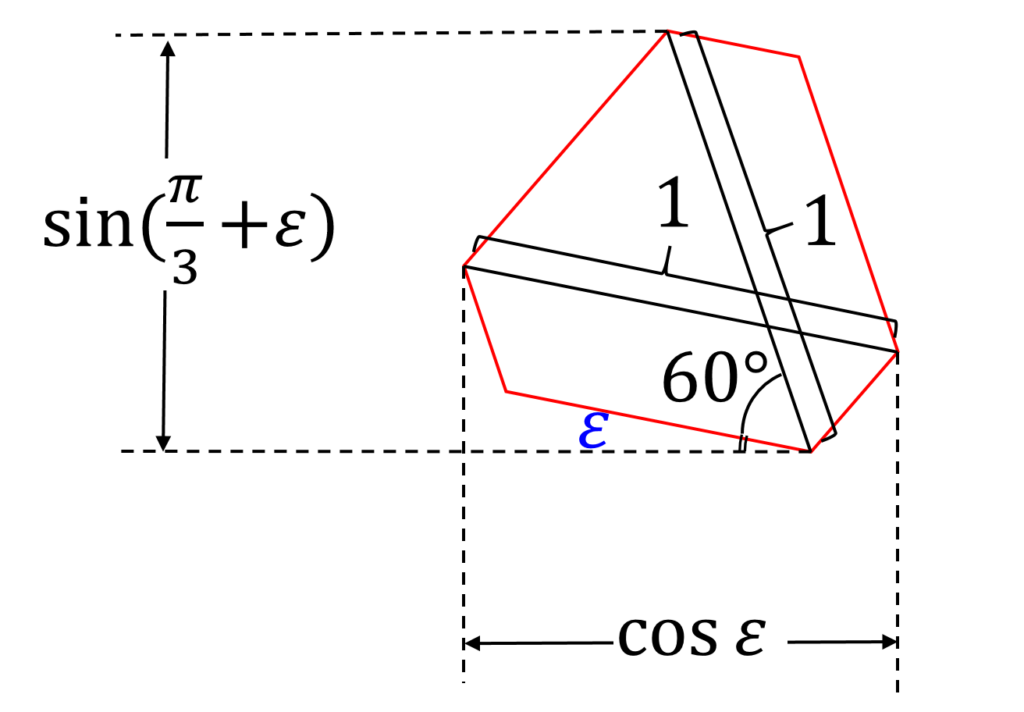
断面の図形を、頂点の一つを軸として \epsilon (0 < \epsilon < \frac{\pi}{6} ) 回転させたとき、断面は高さ h = \sin{ ( \frac{\pi}{3} + \epsilon ) } 、幅 w = \cos{ \epsilon} の矩形に含まれる。
ここで \sin{\epsilon} < 2 - \sqrt{3} となるように \epsilon を定めると、
h = \frac{\sqrt{3}}{2} \sin{ \epsilon } + \frac{1}{2} \cos{ \epsilon } < \frac{\sqrt{3}}{2} + \frac{1}{2} (2 - \sqrt{3}) < 1
w = \cos{ \epsilon} < 1
であるので、断面は常に1辺1の正方形の中に入る。したがって、 V は穴を通過できる。
などという感じにまとめるとよいでしょう(図8参照)。
ちなみに、断面の周の長さが一定であるという、小問1の結果は、使いませんでした。
まとめ
本問は題意の図形のイメージがつかめれば、簡単に解けますが、そのイメージをつかむというのが、難儀です。本問のように、空間図形が題材の問題の場合、図形の各面を個別に取り出して、題意に沿って加工してみるとか、あるいは展開図を書いてみるといった方法が、有効です。
空間図形に対する感覚を高めるのは、なかなか容易ではありませんが、空間図形に関する問題に遭遇した時に、それを解いた後に問題とは別に、図形の鳥瞰図を、いろいろな方向から書いてみる、というようなことを普段からやっておくと、良いのではないかと思います。