2023年 共通テスト 数2B 雑感
本稿は２０２３年共通テストの数II・数Bに関する雑感です。問題文および解答は、以下のリンク先をご覧ください。
ざっと見た感じでは、数１Aより易しい感じです。実際、平均値も数1Aより上です。そちらで目についた、問題文の妙な飛躍（無茶振り）もあまりありません。
応用面を意識した設問
問題文が長いのは相変わらずですが、論理思考力云々という観点よりも、実生活で数学がどのように活用できるかに、よりフィーチャーしているように見受けられます。選択問題の大問４などは、普段やっている利回り計算そのものです。数学の実学的側面を強く意識させようという出題方針なのでしょう。ただし、応用に至るまでの思考過程は問題文によって誘導されていますので、思考力の評価につながるかといえば、それは微妙だと思います。
桜の開花時期予測の問題は、少々やり過ぎか
大問２の（２）は、積分を使って桜の開花時期を予測しようと言う問題です。
気温の累積値がしきい値を超えると桜が開花するというのは、たとえば以下のリンク先に載っています。
グラフの累積値をを積分して求めるという発想は、積分の本質に関わるにもかかわらず、学校では余り取り上げないだけに非常に重要なのですが、桜の開花予測に関して言えば、上記のリンク先にもあるように、毎日の最高気温を足していくだけで事足ります。わざわざ積分を持ち出すまでもないというところが、いささか微妙というか、ちょっとアレな感じです。
本問は積分値を求めることがゴールなので、気温グラフを積分可能な一次関数で近似します。ポイントは気温グラフの積分と一次関数の積分値が一致するように一次関数を決めなければならないことで、単なる積分の計算よりもこちらのほうが遥かに重要です。
ところが本問では、それをしれっと華麗にスルーして、「天才」太郎さんがいきなり出してきた一次関数の式を、単に積分するだけになっています。
更には、２月の気温は１次関数で近似するが、３月の気温は２次関数で近似する流れになっています。これはどう見ても、２次関数の積分を計算させたいためにこじつけているとしか思えません。
結局、単なる計算問題をそれらしく飾っただけとも言えるので、実際の対応としては、問題文に従って淡々と計算していく、ということになります。志は高そうなだけに少々残念、ていうか、受験生サイドからは煩雑なだけのいささか迷惑な出題と言えるでしょう。
ちなみに、近似用の一次関数は最小二乗法によって求められる回帰直線です。元のグラフとの積分値の一致については、「残差の平均が０」という性質から担保されます。回帰直線が履修範囲かどうかは微妙ですが、エクセルを使って簡単に求められるので、問題文に「表計算ソフトを使って求めた」とか書いてあれば、応用的には嬉しい配慮であったと言えるでしょう。
統計の問題は狙い目
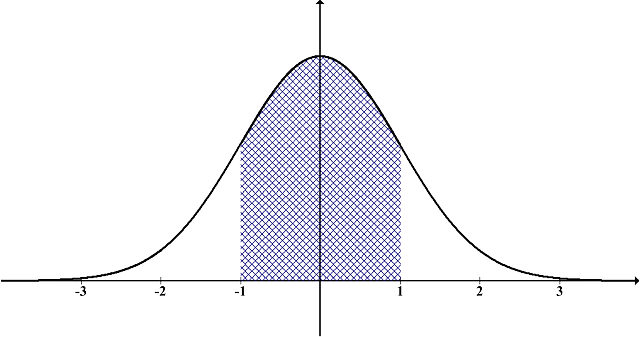
大問３は選択問題で、統計の問題です。正規分布表という禍々しい物がでんと居座っていて、何か恐ろしい暗黒の力を感じます。見なかったことにしてスルーしたいところですが、実は本問は、見た目よりも難しくありません。実際、以下の２点が押さえてあれば、全問中もっとも簡単です。
- 中心極限定理
- ２項分布の平均と分散
来年以降も同様の傾向である場合に備えて、統計の基礎はきちんとさらっておきましょう。統計の知識は社会に出た後でも、数字をいじる職場なら必ず役に立ちます。無駄にならないのでしっかり勉強しておきましょう。
試験対策
基本的な対策は数１Aの場合と同じで、とにかく量が多いので問題をたくさんこなして、速さと正確さを身につけるようにしましょう。
また、出題傾向が来年度も同じ場合に備えて、統計の勉強はきっちり行っておきましょう。