定積分を求めてみる
そもそも本当に、 \int_0^{\pi} e^x \sin^2 x dx は計算できないのでしょうか。被積分関数に積分しても微分しても変化しない e^x が含まれているので、部分積分してみろと数学の神が呼んでいるぞ。
そんなわけで、定積分の値を具体的に計算してみます。
もとめる定積分を I と置く時、
\begin{aligned}
& I = \int_0^{\pi} e^x \sin^2 x dx \\
& = \left[e^x \sin^2 x \right]_0^ \pi - 2\int_0^{\pi} e^x \sin x \cos xdx \\
& = -\int_0^{\pi} e^x \sin 2x dx \\
& = - \left[e^x \sin2 x \right]_0^ \pi + 2\int_0^{\pi} e^x \cos2 xdx \\
& = 2 \int_0^{\pi} e^x (1- 2\sin^2 x )dx \\
& = 2 \int_0^{\pi} e^x dx - 4 \int_0^{\pi} e^x \sin^2 x dx \\
& = 2(e^{\pi} -1) - 4I
\end{aligned}したがって、
I = \frac{2}{5}(e^{\pi} -1 )と、あっさり計算することが出来ました。
ここまで来れば、あとは \pi, e の近似値を右辺に代入すれば、題意がさくっと証明できると期待が高まります。
問題文で e = 2.71 \cdots と近似値が与えられているので、これを使って計算します。 \pi のほうは、小数が指数の時の計算方法がよくわからないので、3で近似します。
ところが、
\begin{aligned}
& \frac{2}{5}(e^{\pi} -1 ) \\
> & \frac{2}{5}(2.71^3 -1 ) \sim 7.56
\end{aligned}となり、評価値はまだガバガバでした。世の中そんなに甘くないようで、指数関数の近似をもっと真剣に考えなければならないようです。
e^{\pi} の近似値を求める
証明すべき I > 8 は、
e^{\pi} > 21と同値なので、これの証明を目指します。
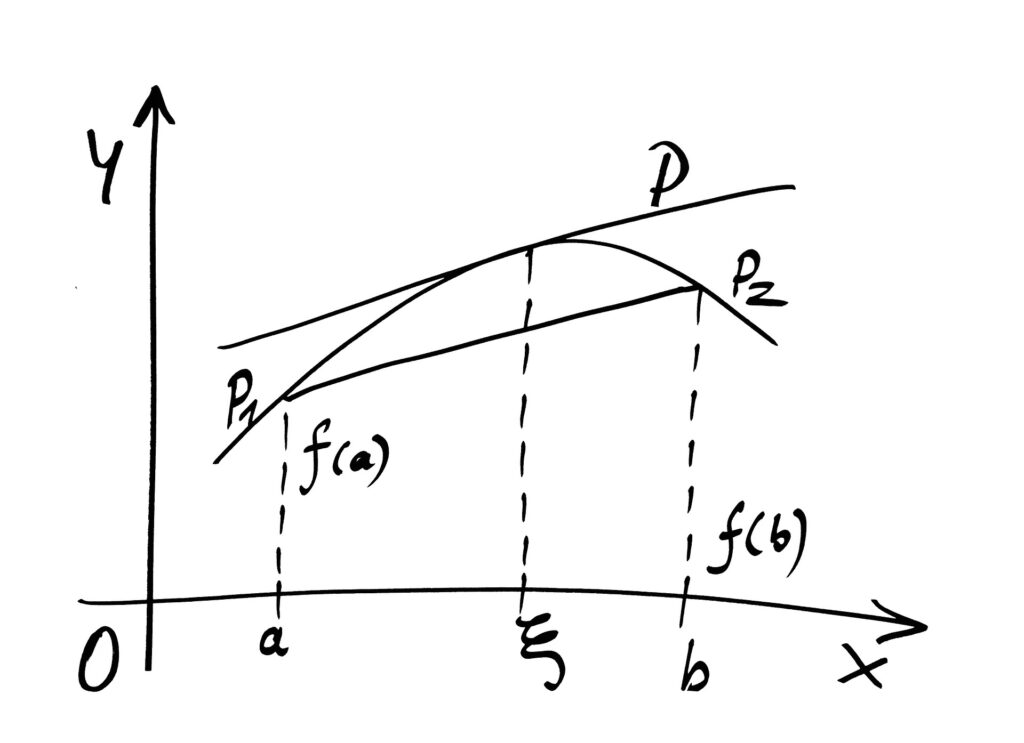
e^x に対して 3 < x < \pi の範囲に平均値の定理を適用します。ある実数 c \text{ } (3< c< \pi) が存在して
\frac{e^{\pi} -e^3}{\pi-3} = e^c > e^3なので、
\begin{aligned}
e^{\pi} & > (\pi-3)e^3 + e^3\\
& = ( \pi -2) e^3\\
&> (3.14-2)\times2.71^3 \\
& \sim 22.68> 21
\end{aligned}と、今度こそ証明できました。
解法のポイント
本問は定積分の近似値を求める体裁をとっていますが、具体的な値を解析的に求めることが出来るので、本質的には
e^{\pi} > 21の証明と言う、積分とは無関係の問題に帰着できます。最初の積分は単なる目くらましにすぎず、いささか意地の悪い設問とも思えますが、そこはやはり、アンゴルモアの大王の年だからと言うことなのでしょう(そんな訳ない)。
定積分の値を、積分挟み撃ちの技法で近似しようとする場合は、被積分関数の値が容易に計算できるかどうかに着目してください。本問のように計算が面倒な場合や、値それ自体は簡単に求められても、和を取る時に計算が面倒くさくなる場合は、他のアプローチが正しい公算が大きいと考えられます。
また、平均値の定理を近似に適用する際には、変域が十分に小さいことが必要になります。本問での変域は 3 < x < \pi で、その幅 \delta は0.14くらいですが、できるだけ \delta が小さくなるように考慮してください。