小問2の解法
空間図形 W の形状を把握する
線分 OP が1回だけ屈曲でき、屈曲点がNです。イメージとしては、 O に無数のチュッパチャプスが刺して有って、飴の部分の中心が N 、飴の表面および内部に P がある、と言った感じです(図7)。
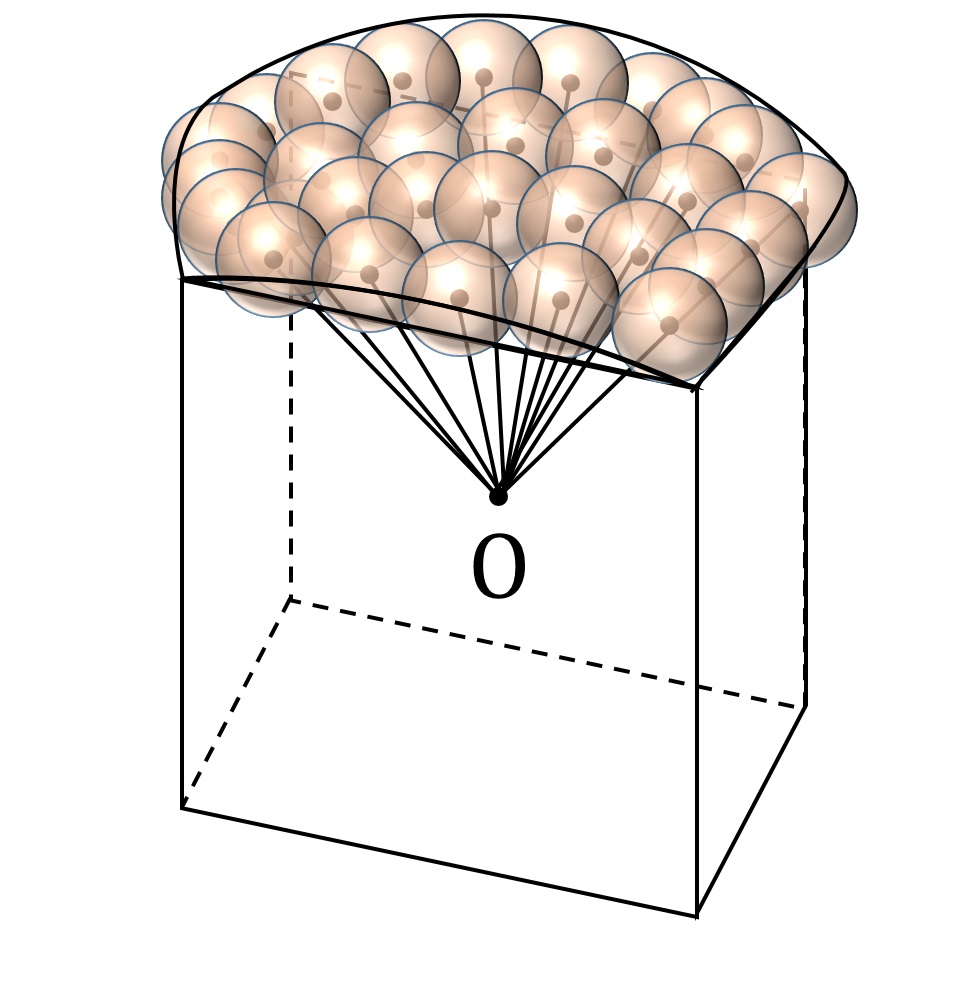
当然、V は W に含まれますので、 W は V のどこから外に張り出しているのかを明確にします。
小問2の条件でも箱 S を突破することは出来ないので、ここから外に染みてくることはありません。また、 ON + NP は球面の半径以下なので、球面の外に出ていくことも出来ません。
よって、V から外に出られるのは、4つある側面の円弧部分となります(図8)。
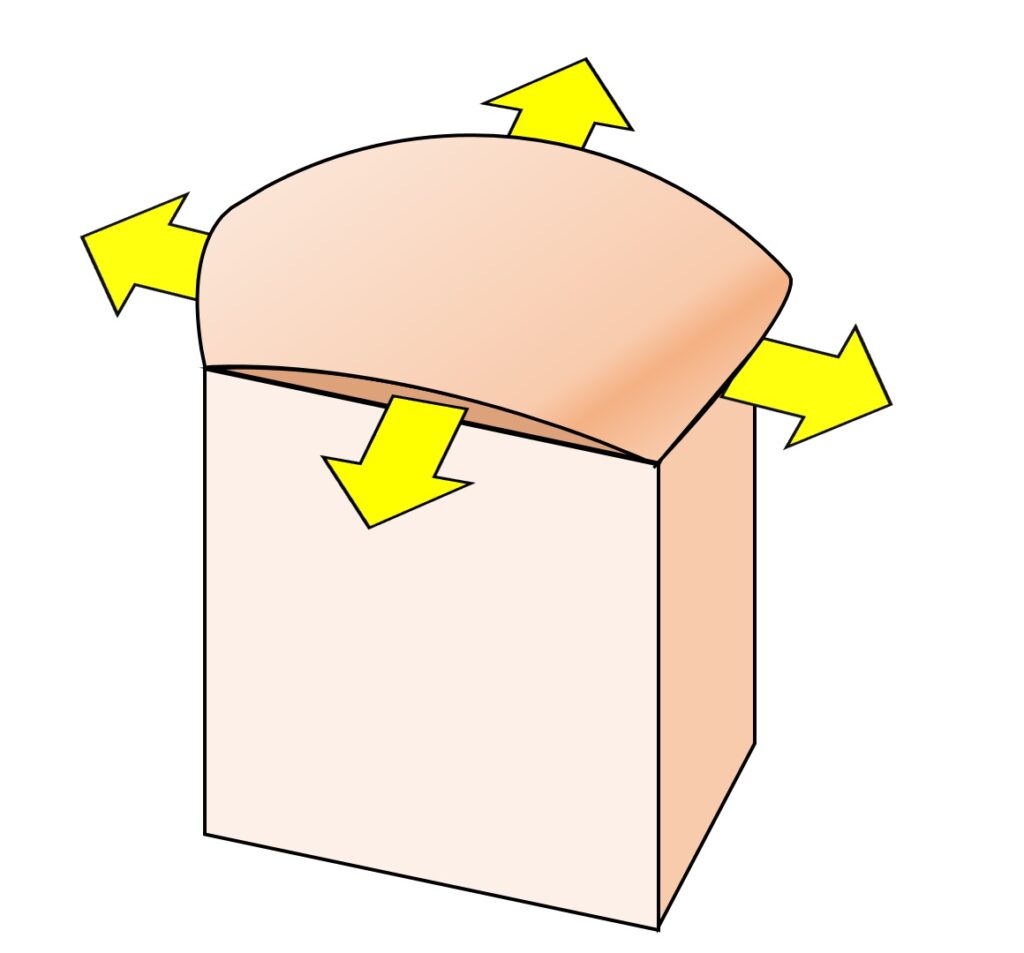
ここで、 P が最も外に到達できるのは、 N が箱 S の「縁」(正方形 |x| =|y| =1,z=1 )にあることを証明します。
P が V の外側にあるとき、 NP と側面円弧との交点を Q 、その側面円弧と S との交線(すなわち側面円弧の弦)を l とします。このとき、線分 OQ と l は明らかに同一平面上にあり、しかも交点を持ちます。その交点を M と置きます(図9)。

すると、三角不等式により
\begin{aligned}
& \rm{OM} + MP \\
\leqq & \rm OM + MQ +PQ \\
= & \rm OQ + PQ \\
\leqq & \rm ON + NQ + PQ \\
= & \rm ON + NP \\
\leqq & \sqrt 3
\end{aligned}なので、
\rm MP \leqq \sqrt 3 - OM
です。すなわち、点 P をどのように選んでも、箱 S の縁 l 上の点 M が存在して、P は M を中心とする半径 \sqrt 3 - \rm OM の球面に包含されるので、P が最も外に到達できるのは、 N が箱 S の縁にあるときであることが証明できました。
以上の考察により、 N が箱 S の縁にあるときのみを考えれば良いことがわかりました。
張り出し部分の体積を求める
屈曲点 N が辺 l 上にあるときだけを考えれば良いので、張り出し部分は縁 l を軸とした回転体と予想できます。
よって、 l に沿って断面積を積分すれば体積を求められるので、断面積の式を求めます。
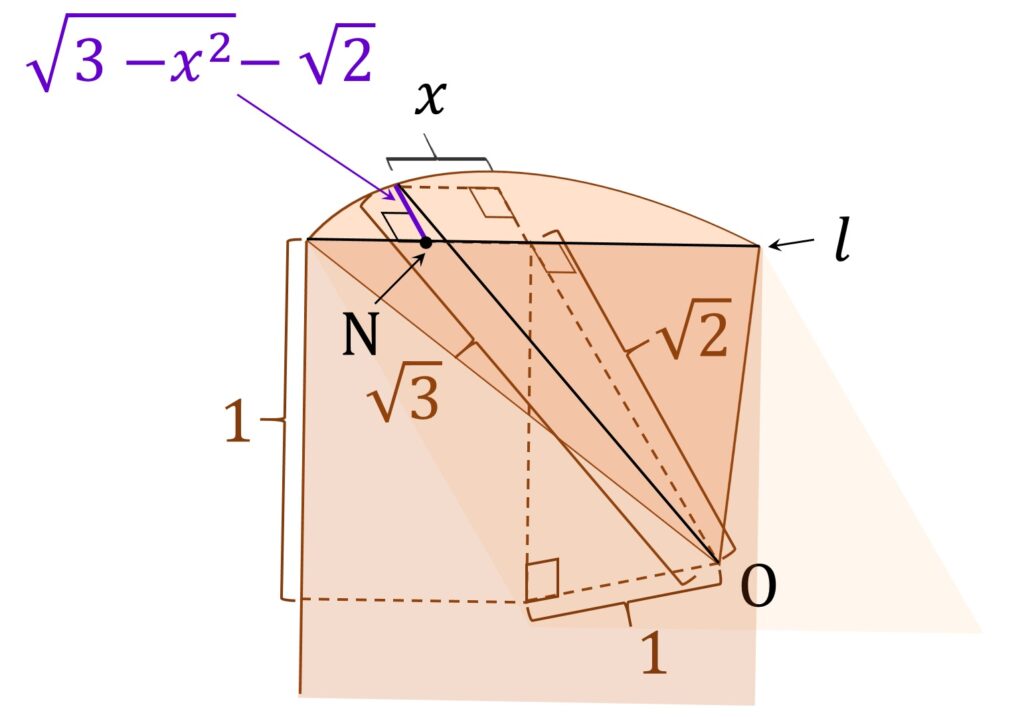
縁の正方形のうちの1辺 l = \{ (x,y,z) \in \mathbb{R} ^3 | |x| \leqq 1,y =1,z=1 \} 上で考えます。
点 N の座標を (x,1,1) と置くとき、 \rm ON = \sqrt {x^2 +2} なので、N を通り l に垂直な平面における張り出し部分の断面は、半径 \sqrt 3 - \sqrt{x^2 +2} 、中心角 \displaystyle\frac{3 \pi}4 の扇型であり、求める体積は、同じものが4つあるので
\begin {aligned}
& \frac{3 \pi}8 \int_{-1}^1 (\sqrt 3 - \sqrt{x^2 +2 })^2 dx \times 4 \\
= & 3 \pi \int_{0}^1 (\sqrt 3 - \sqrt{x^2 +2 })^2 dx
\end{aligned}です。
後はこれを計算するだけですが、計算方法がよくわからないことの他に、問題文の条件「 \sin \alpha = \displaystyle\frac 1{ \sqrt{3}} を満たす実数 \alpha \displaystyle\left( 0 < \alpha < \displaystyle\frac{\pi}2 \right ) を用いてよい」を使わないで済んでいるところが、なんか怪しいです。
そもそも、側面円弧と張り出し紡錘形がシームレスに繋がっていないというのも、嘘くさいところです。 N を通り、l に垂直な平面で側面円弧を切断したときの長さは
\sqrt {3 - x^2} -\sqrt 2です(図10)。
明らかに \sqrt 3 - \sqrt{x^2 +2} と異なり、側面円弧の面で段差が生じます。
ここまで考えたところで、張り出し部分は側面円弧を l を軸にして \displaystyle\frac{3 \pi}4 回転させた、部分回転体ではないだろうか、と予想できます(図11)。
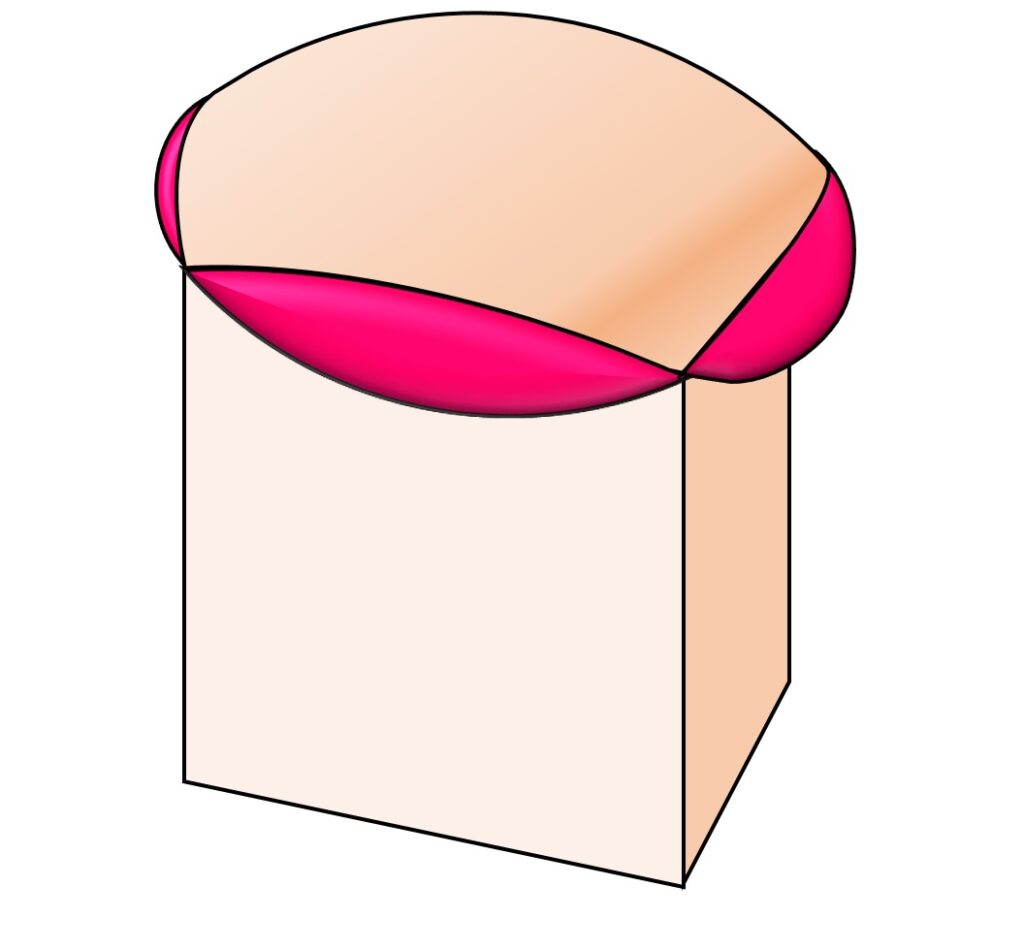
すなわち、 N を通り l に垂直な平面における張り出し部分の断面は、半径が \sqrt {3 - x^2} -\sqrt 2 で、中心角 \displaystyle\frac{3 \pi}4 の扇型 Sec(x) であると予想できます。
以下、それを証明します。
側面円弧の平面を H と置きます。このとき、O と l は H 上に有ります。また、N を通り、 l と垂直な平面を I(x) と置きます(図12)。

P を、 I(x) 上の点であるとします。
\mathrm{P} \in Sec(x) のとき、
\mathrm{NP} \leqq\sqrt {3 - x^2} -\sqrt 2ですが、 H 上の点 P’ を、
\begin{aligned}
& \rm NP' = \rm NP \text{ かつ}\\
& \mathrm {NP' } \perp l \text{ かつ} \\
& \mathrm P \text{は} l \text{をはさんで} \rm O \text{と反対側}
\end{aligned}を満たすように置き、 M を OP’ と l の交点とするとき、明らかに MP = MP’ であり、また \rm OP' \leqq \sqrt 3 なので
\begin{aligned}
& \rm OM + MP \\
= & \rm OM + MP' \\
= & \rm OP' \\
\leqq & \sqrt 3
\end{aligned}であり、したがって \mathrm{P} \in W です(図13)。

次に、 \mathrm{P} \notin Sec(x) であるとします。このとき、
\mathrm{NP} > \sqrt {3 - x^2} -\sqrt 2ですが、もし \mathrm{P} \in W であるとすると、張り出し部分は N が箱 S の縁にあるときのみを考えれば良いことを示した時の議論により、 l 上の点 M が存在して、
\rm OM + MP \leqq \sqrt 3
が成り立ちます。
ここで、 H 上の点 P’ を、
\begin{aligned}
& \rm NP' = \rm NP \text{ かつ}\\
& \mathrm {NP' } \perp l \text{ かつ} \\
& \mathrm P \text{は} l \text{をはさんで} \rm O \text{と反対側}
\end{aligned}を満たすように置くと、
\rm OP' > \sqrt 3
です(図14)。

一方でMP = MP’ なのと、三角不等式により OP’ ≦ OM + MP’ なので、
\rm OP' \leqq OM + MP' = OM +MP \leqq \sqrt 3
となり、矛盾が発生します。よって、 \mathrm{P} \notin W です。
したがって、 平面 I(x) の点 P が \mathrm{P} \in Sec(x) であることと \mathrm{P} \in W であることは同値であり、張り出し部分を I(x) で切断した断面は Sec(x) です。
Sec(x) の面積は
\begin{aligned}
& \frac{3 \pi}8 ( \sqrt {3 - x^2} -\sqrt 2)^2 \\
= & \frac{3 \pi}8 ( 5 -x^2 -2 \sqrt 2 \sqrt {3 - x^2})
\end{aligned}なので、張り出し部分の体積は、同じものが4つあることを考慮して
\begin{aligned}
& \int_{-1}^1 \frac{3 \pi}8 ( 5 -x^2 -2 \sqrt 2 \sqrt {3 - x^2}) dx \times 4 \\
= & 3 \pi \int_0^1 ( 5 -x^2 -2 \sqrt 2 \sqrt {3 - x^2}) dx \\
= & 3 \pi \left [ 5x - \frac{x^3}3 \right ]_0^1 - 6 \sqrt 2 \pi \int_0^1 \sqrt {3 - x^2}) dx \\
= & 14 \pi -18 \sqrt 2 \pi \int_0 ^ {\alpha} \sqrt{1 - \sin^2 \theta} \cos \theta d \theta \\
= & 14 \pi -18 \sqrt 2 \pi \int_0 ^ {\alpha} \cos^2 \theta d \theta \\
= & 14 \pi -18 \sqrt 2 \pi \int_0 ^ {\alpha} \frac{1 + \cos 2 \theta} 2 d \theta \\
= & 14 \pi - 18 \sqrt 2 \pi \left [ \frac{\theta}2 + \frac{ \sin 2 \theta}4\right ]_0^{\alpha} \\
= & 14 \pi - 9 \sqrt 2 \pi \alpha - \frac{9 \sqrt 2 \pi \sin 2 \alpha}2 \\
= & 14 \pi - 9 \sqrt 2 \pi \alpha - 9 \sqrt 2 \pi \sin \alpha \cos \alpha\\
=& 14 \pi - 9 \sqrt 2 \pi \alpha - 9 \sqrt 2 \pi \cdot \frac1{\sqrt{3}} \cdot \sqrt{\frac {2} 3} \\
= & 8 \pi - 9 \sqrt 2 \pi \alpha
\end{aligned}です。ここに \alpha は問題文の \alpha で、 \sin \alpha = \displaystyle\frac1{ \sqrt 3} が成り立ちます。
ゆえに W の体積は
\begin{aligned}
& \frac{2 \sqrt{3} \pi}{3} + \frac{20}3 + 8 \pi - 9 \sqrt 2 \pi \alpha \\
\end{aligned}です。
解法のポイント

本問の難しいところは、体積を求めるための方針がなかなか立てられないことにあります。数式も与えられていないので、こういうときには図形のイメージをつかむことがポイントです。
小問1は本稿で示したように、コーン部分が球体の \frac {1} 6 であることに気がつくことが重要ですが、立方体が球に内接しているところから、バレーボール的なものが連想できると正解に近づけます。
小問2の方は、点 P が最も外に張り出すのは屈曲点 N が箱 S の縁に乗っているだと気がつくのが第1歩ですが、これは感覚的には明らかだと思います。
ここから、積分に持って行くまでがまた大変ですが、屈曲点 N が箱 S の縁に乗っているというところから、張り出し部分は小問1の V の側面円弧を、箱 S の辺を軸にして回転したものだと気がつければ、ゴールは目前です。
東大の空間図形問題は難問揃いですが、過去問に出てくる図形を自分で描画するなどして、図形に関する感覚を養うようにしてみましょう。