3次関数グラフの対称性に着目する
h(x) は3次関数ですが、3次関数は1つだけある変曲点を中心とした点対称です。特に、極大となる点と極小となる点の中点が変曲点になります。
したがって、極大値が 1 、極小値が -1 であることから、変曲点の y 座標は 0 です。すなわち、変曲点の x 座標を β と置くとき、 β は方程式 h(x) = 0 の実数根であり、 h(x) は x - \beta で割り切れます。
明らかに h(x) =0 は実数根を3つ持ちます。 x = \beta 以外の2つの実数根は、グラフの対称性から β からの距離が等しいので、その距離を α ( α > 0 ) と置くと、 h(x) は
h(x) = p (x- \beta)(x-\beta + \alpha)(x-\beta- \alpha)
と因数分解できます。 p > 0 だったので、 h(x) のグラフは左下から上がってきて右上に抜けていきます(図1)。
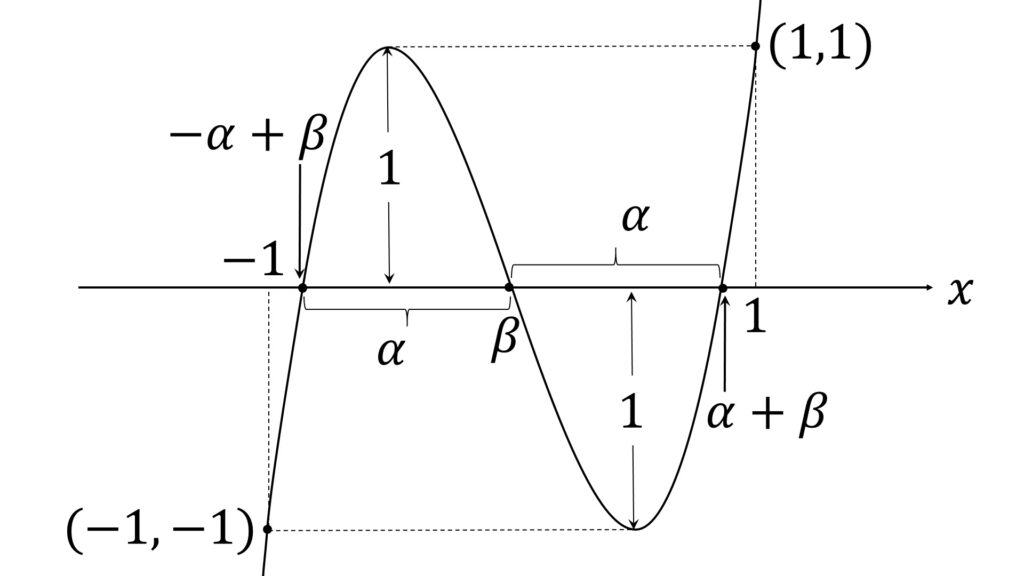
図1から明らかなように、 α < 1 です。
変曲点の x 座標 β が 0 であることを証明する
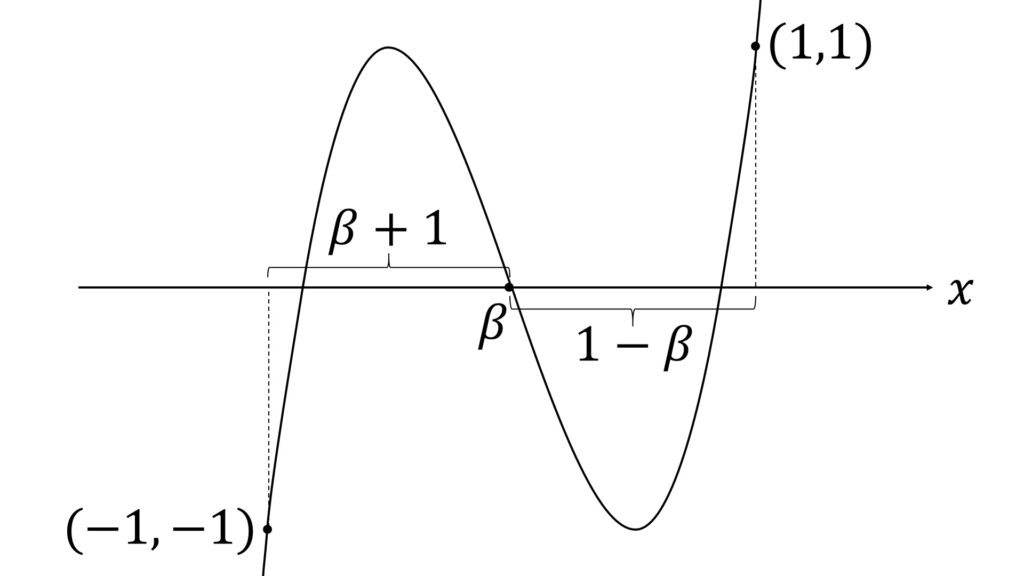
y = h(x) のグラフが (-1,-1) および (1,1) を通ることと、2点の y 座標の平均が変曲点の y 座標である 0 に等しいことから、2点は変曲点 ( β ,0 ) に対して対称の位置に有り、したがって
1 - \beta = \beta -(-1)
であり、ゆえに β = 0 です(図2)。
などと、時間がないときは(多分時間が全然足りないはずなので)、これで強行突破しても天下の東大だし、3次関数の細かい性質にくどくど言わずにそこそこの点はもらえると思います。何しろ言っていることは正しいのだし。
これをきちんと証明する場合は、以下のようになります。
h(1) +h(-1) = 0
なので、
\begin{aligned}
& p (1- \beta)(1-\beta + \alpha)(1-\beta- \alpha) \\
+ & p (-1- \beta)(-1-\beta + \alpha)(-1-\beta- \alpha) \\
= & 0
\end{aligned}です。 p > 0 なので両辺をこれで割って
\begin{aligned}
& (1- \beta)(1-\beta + \alpha)(1-\beta- \alpha) \\
+ & (-1- \beta)(-1-\beta + \alpha)(-1-\beta- \alpha) \\
= & 0
\end{aligned}です。これを展開して
\begin{aligned}
& (1- \beta)^3 -\alpha^2(1-\beta ) \\
- & (1+ \beta)^3 + \alpha^2(1+\beta ) \\
= & 0
\end{aligned}です。したがって、
-6 \beta -2 \beta^3 +2 \alpha^2 \beta = 0
であり、左辺を β でくくって2で割って、
\beta ( \beta^2 -\alpha^2 +3) = 0
が成り立ちます。
0 < α < 1 であったので、 \beta^2 - \alpha^2 +3 > 0 です。ゆえに、 β = 0 です。
β = 0 の証明自体はそんなに難しくありませんが、やり方を思いつくのはちょっと大変かもしれません。
α および p を求める
ここまでの議論により
\begin{aligned}
h(x) &=px(x- \alpha)(x+ \alpha) \\
& = px(x^2-\alpha^2)
\end{aligned}であることがわかりました。
関数 h(x) が極大値を取る時の x の値は x = - \displaystyle\frac{\alpha}{\sqrt{3}} なので、
h \left (-\frac{\alpha}{\sqrt{3} } \right) = h(1) が成り立ちます。よって
-p\frac{\alpha}{\sqrt{3}}(\frac{\alpha^2}3- \alpha^2) = p(1-\alpha^2)整理して
2 \alpha^3 +3\sqrt{3} \alpha^2 - 3 \sqrt{3} = 0を得ます。
3次方程式の解の公式なんて知らないし、これはバンザイかとも思いましたが、入試問題なんだしそんなに無茶はしないはずだから、左辺は案外因数分解できるかも知れません。
因数分解できるとしたら解は分数になって、分母は3次の項の係数2の約数、分子は定数項 3 \sqrt{3} の約数です。 α は正なので分母の候補は1か2、分子の候補は 1, \sqrt{3} ,3, 3 \sqrt{3} のいずれかとなります。
α < 1 なので、α の候補としては
\alpha = \frac{1}2,\alpha= \frac{\sqrt{3}}2の2つが考えられます。
まず \alpha = \displaystyle\frac{1}2 で試します。
2 \left ( \frac{1}2 \right) ^3 + 3 \sqrt{3} \left ( \frac{1}2 \right) ^2 - 3 \sqrt{3} = \frac{1}4 -\frac{9 \sqrt{3}}{4}でハズレでした。
次に \alpha = \displaystyle\frac{\sqrt{3}}2 で試します。
\begin{aligned}
& 2 \left ( \frac{\sqrt{3}}2 \right) ^3 + 3 \sqrt{3} \left ( \frac{\sqrt{3}}2 \right) ^2 - 3 \sqrt{3} \\
= & \frac{3\sqrt{3}}4+ \frac{9\sqrt{3}}4 -3 \sqrt{3} \\
= & 0
\end{aligned}でビンゴです。
他に候補がないかどうか、調べます。
\begin{aligned}
& 2 \alpha^3 +3\sqrt{3} \alpha^2 - 3 \sqrt{3} \\
= & (2 \alpha -\sqrt{3})(\alpha^2+ 2 \sqrt{3} \alpha +3) \\
= & (2 \alpha -\sqrt{3})( \alpha + \sqrt{3})^2
\end{aligned}と因数分解できるので、他の解は \alpha = - \sqrt{3} ですが、これは負なので対象外です。
したがって
\alpha = \displaystyle\frac{\sqrt{3}}2です。
残りは p の値です。最初の方に出てきてもうすっかり忘れてしまっていますが、 p + r = 1 でした。 r = – pα2 なので、
p - p \alpha^2 = 1
ですが、ここからただちに
p = 4
を得ます。ゆえに
h(x) = 4 x^3 - 3x
です。