簡単そうで実は激ムズな3次関数問題 – 1990年東大 数学 第2問

2023年9月23日2023年12月21日

1990年東大 数学 第2問 小問2の解法

f(x) の係数が満たすべき条件からアプローチしてみる

　 -1< x < 1 の範囲で -1 < f(x) < 1 という条件から、 f(x) の係数 a,b,c,d が満たすべき条件を導き出し、これから問題文の不等式が成り立つことを証明する、というのがまず思いつく方針です。

　長くなるので割愛しますが、この方法だと、 f(x) の極値が |x| < 1 の範囲にある場合とない場合に分けるなど、場合分けが大変で計算がドロドロになります。小問２についても、もっと楽な方法がないかどうか、考えてみます。

f(x) の係数の具体的な条件を求めない解き方を考える

　 x > 1 のとき h(x) > 0 であり、 x < -1 のとき h(x) < 0 であるので、 |x| >1 の範囲で |f(x) | < |h(x)| であるということは、

\begin{aligned} 
 & x > 1 \text{のとき　} & -h(x) <  & f(x) < h(x) \\
  &\text{　　　　かつ}  \\
 & x  < -1 \text{のとき　}  &h(x) <   &f(x) < -h(x) \\
\end{aligned}

であることと同値です。

　つまり、 |x| > 1 の範囲で |f(x) | < |h(x)| であるならば、その範囲で h(x) と f(x) の大小が変らないので、 h(x) と f(x) は交点を持ちません。

　すなわち、 |x| > 1 の範囲で h(x) と f(x) が交点を持たないことは、 |x| > 1 の範囲で |f(x) | < |h(x)| であるための必要条件です。

　 -1 < x < 1 で -1 < f(x) < 1 を仮定するとき、まずはこの必要条件が成り立つことを証明したいところですが、それはちょっとハードルが高そうです。普通は微分して増減表を書く、と言ったアプローチになりますが、係数が未定の状態では泥沼は必定でしょう。

　いろいろ考えているうちに、そう言えば |x| \leqq 1 の範囲で h(x) と f(x) の交点の数はどうなっているのだろうか。こちらのほうが簡単に評価できそうだし、何か言えればそれがヒントになるかも知れない、と思いつきました。

　まあ、交点は１つくらいはありそうだなと思いますが、ここで h(x) が 1 と -1 の間を正確に３回行き来することに着目します。連続関数 f(x) が |x| < 1 の範囲で |f(x) | < 1 なのだから、 |x| \leqq 1 の範囲で |f(x) | \leqq 1 になることが何となく言えそうです（後で証明します）。よって、 |x| \leqq 1 の範囲で最低でも３個交点があるはずだ、と気がつければもう解けたも同然です(図３)。

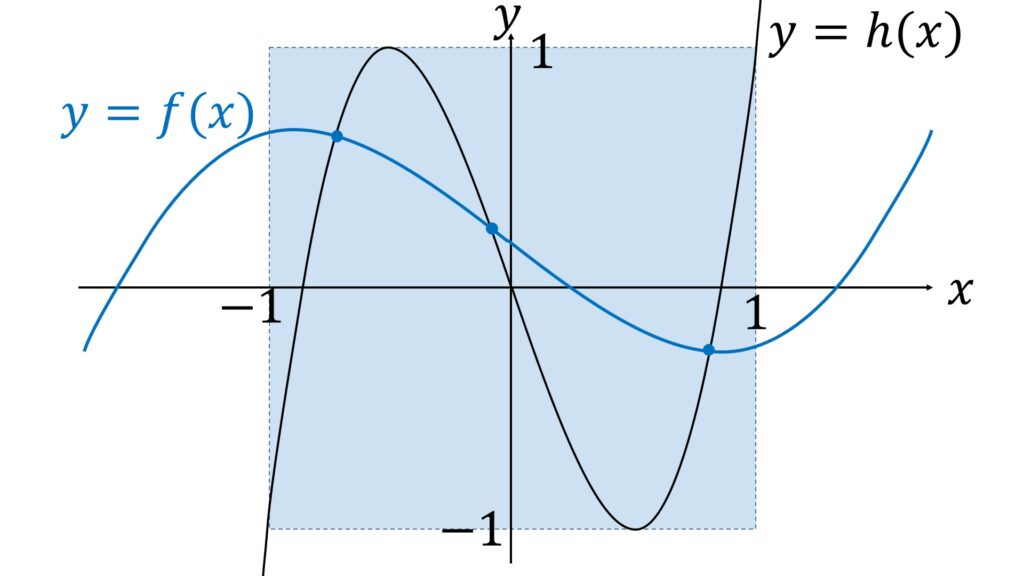
　 f(x) も h(x) も３次関数なのだから、交点の数はたかだか３個です。 |x| \leqq 1 の範囲で交点が３個あるのだから、当然その外側では交点は０個です。

　ここで |f( \pm 1) | < 1 を仮定すると、 |f(\pm1) | < |h(\pm 1) | = 1 です。 |x| > 1 のとき、 h(x) と f(x) の交点は０個なのですから、 |x| \geqq 1 の範囲でも交点は０個です。よってこの範囲で、２関数の大小関係は入れ替わりません。したがって、 |f(x) | < |h(x) | です。

　 f(\pm1) の値の評価については積み残しがありますが、だいたい証明できそうなめどが立ちましたので、以下、中間値の定理を利用して証明を組み立てます。

中間値の定理を利用して証明する

\begin{aligned} 
 & x > 1 \text{のとき　} & -h(x) <  & f(x) < h(x) \\
    & & \text{かつ　　}  \\
 & x  < -1 \text{のとき　}  &h(x) <   &f(x) < -h(x) \\
\end{aligned}

を言い換えると、

\begin{aligned} 
 & x > 1 \text{のとき}  &  \left \{ \begin{aligned} h(x) - f(x) > 0 \\ h(x) + f(x) > 0   \end{aligned} \right .\\
  &\text{　　　　かつ}  \\
 & x  < -1 \text{のとき} &  \left \{ \begin{aligned} h(x) - f(x) < 0 \\ h(x) + f(x) < 0   \end{aligned} \right . \\
\end{aligned}

です。そこで、

F(x) =h(x) -f(x) \\
G(x) = h(x) + f(x)

とおくとき、

\begin{aligned} 
 & x > 1 \text{のとき}  & F(x) > 0 \text{　かつ　} G(x) > 0 \\
   && \text{かつ　　　　　　　　　}  \\
 & x  < -1 \text{のとき}   & F(x) < 0 \text{　かつ　} G(x) < 0 \\

\end{aligned}

が成り立つことを証明します。これが成り立つことと |x| > 1 のとき |f(x) |< |h(x) | が成り立つことは同値です。

　以下、 |x| \leqq 1 の範囲で |f(x) | \leqq 1 であると仮定します。 f(x) が連続関数であることと、 |x| < 1 の範囲で |f(x)| < 1 であることから明らかな気がしますが、連続関数について学校でどこまで教えているのか不安なので、後で証明します。

　 h(x) =4x^3 -3 x は x = - \displaystyle\frac{1}2 のとき極大値 1 を、 x = \displaystyle\frac{1}2 のとき極小値 -1 を取ります。また、 h(-1) = -1, h(1) = 1 であることから、

\begin{aligned}
F(-1) & = h(-1) -f(-1) =-1-f(-1)\leqq 0, \\
 F(-\frac{1}2) & =h(-\frac{1}2) - f(-\frac{1}2)=1  - f(-\frac{1}2)> 0, \\
F(\frac{1}2) & =h(\frac{1}2) - f(\frac{1}2)= -1 - f(\frac{1}2)< 0, \\
F(1)  &= h(1) -f(1) =1 -f(1)\geqq 0
\end{aligned}

が成り立ちます。

　したがって中間値の定理により、方程式 F(x) = 0 は -1 \leqq x < - \displaystyle\frac{1}2 、 -\displaystyle\frac{1}2 < x < \displaystyle\frac{1}2 、 \displaystyle\frac{1}2 < x \leqq 1 の各区間で、少なくとも１つの解を持ちます。

　ところが F(x) は次数が３次以下の多項式（ f(x) と h(x) の３次の係数が等しい場合もないとは言えないが、その場合は次数が２以下になる）なので、方程式 F(x) = 0 は高々３つの解しか持ちません。よって方程式 F(x) = 0 は -1 \leqq x < - \displaystyle\frac{1}2 、 -\displaystyle\frac{1}2 < x < \displaystyle\frac{1}2 、 \displaystyle\frac{1}2 < x \leqq 1 の各区間で１つずつ解を持ちます。解が３つなので、 F(x) は３次式です。

　それらの解を \xi,\eta,\zeta ( -1 \leqq \xi < -\displaystyle\frac{1}2 < \eta < \displaystyle\frac{1}2 < \zeta \leqq 1) と置くとき、関数 F(x) は

F(x) = A(x-\xi)(x-\eta)(x-\zeta)

と表すことが出来ます（ A は０でない定数）。

　ここで x = \displaystyle\frac{1}2 を代入すると、

F( \frac{1}2) = A(\frac{1}2 -\xi)(\frac{1}2-\eta)(\frac{1}2- \zeta) < 0

であり、かつ

\begin{aligned}
 \frac{1}2 - \xi > 0 \\
 \frac{1}2 - \eta > 0 \\
 \frac{1}2 -\zeta < 0 \\
\end{aligned}

なので、 A > 0 です。

　ゆえに x > 1 のとき F(x) > 0 が成り立ち、 x < -1 のとき F(x) < 0 が成り立ちます。

　上記の議論は f(x) を -f(x) に置き換えても成り立ちます。したがって、 x > 1 のとき G(x) > 0 が成り立ち、 x < -1 のとき G(x) < 0 が成り立ちます。

　以上、 |x| > 1 のとき |f(x) |< |h(x) | であることが証明できました。

|x| < 1 のとき |f(x)| < 1 なら |f(±1)| ≦ 1 であることの証明

　 f(x) の連続性から明らかな気がしますが、念の為証明を準備します。背理法で証明します。

　もし f(1) > 1 ならば、 f(\displaystyle\frac{1}2 ) < 1 なので、 f(x) が連続関数であることと中間値の定理より、ある実数 \displaystyle\frac{1}2 < \epsilon < 1 が存在して、 f( \epsilon) = 1 が成り立つはずですが、これは |x| < 1 のとき |f(x)| < 1 であることに矛盾します。

　よって f(1) \leqq 1 です。同様にして f(1) \geqq -1 が成り立ちます。更に、 -1 \leqq f(-1) \leqq 1 が成り立ちます。

解法のポイント

　小問１は条件がたくさんあるし、代数的手法でさくっと解けるのではないかと思ってしまいがちですが、それは罠です。係数に関する方程式を立てて何とかしようと言う発想を如何にして早く見限るかが、第一のポイントです。高々20〜30分で解かなければならない問題の、しかも小問1で平方根やら二次式やらがごちゃごちゃ出てきたら、これはおかしいと思いましょう。

　ではどうするかですが、本稿に示したようにグラフの形がどうなっているのかに着目するのが、ひとつのアプローチです。与えられた条件から y = h(x) のグラフが原点を通りそうだと気がつければ、半ば解けたようなものです。

　本稿では無理数係数の3次方程式を解く羽目になって、いささか焦りましたが、[math]1990年東京大学理系前期数学問題2では違ったアプローチで解いていますので、ご覧ください。こちらのリンク先でも、グラフを書いてみることを推奨しています。

　小問2も、各係数の具体的な条件を求めようとするとハマります。 本稿に記述したように、 |x| > 1 のときに |f(x) |< |h(x) | であることを証明するためには、その区間において2つの関数の交点がないことを証明することが必要だと気がつくことと、そこから |x| \leqq 1 の範囲で2つの関数が3つの交点を持つこと、およびそれを中間値の定理を使って証明できることに気がつくことがポイントです。

　なお、小問1が解けなくても小問2を解くことは可能です。小問1を解くのにえらい苦労するだけに、何ともシニカルな問題構成ですが、気がつければ大金星です。そのようなラッキーを拾えるかも知れないので、関数の大小を証明するような問題の場合、代数的アプローチや微分を使用する方法の他に、本稿で示したような連続関数の性質を利用する方法があることを念頭に置いておきましょう。攻め手のバリエーションが広がります。