2024年東大 数学 第3問は二次元座標空間上の点がある規則で移動するときの存在確率を求める問題です。問題文は以下のとおりです。
座標平面上を次の規則 (A) , (B) に従って1秒ごとに動く点 P を考える.
(A) 最初に、 P は点 (2,1) にいる.
(B) ある時刻で P が点 (a,b) にいるとき,その1秒後には P は
・確率 \displaystyle\frac{1}3 で x 軸に関して (a,b) と対称な点
・確率 \displaystyle\frac{1}3 で y 軸に関して (a,b) と対称な点
・確率 \displaystyle\frac{1}6 で直線 y = x に関して (a,b) と対称な点
・確率 \displaystyle\frac{1}6 で直線 y = –x に関して (a,b) と対称な点
にいる.以下の問いに答えよ.ただし、 (1) については,結論のみ書けばよい.
(1) P がとりうる点の座標をすべて求めよ.
(2) n を正の整数とする.最初から n 秒後に P が点 (2,1) にいる確率と,最初から n 秒後に P が点 (-2,-1) にいる確率は等しいことを示せ.
(3) n を正の整数とする.最初から n 秒後に P が点 (2,1) にいる確率を求めよ.
ぱっと見は、確率漸化式を立てれば何とかなりそうな気がします。それでは見ていきましょう。
2024年東大 数学 第3問 小問1の解法
4つあるオペレーションを、 \mathbb{R}^2 から \mathbb{R}^2 への写像として、順番に以下のように定義します。
\begin{aligned}
f((a,b)) & = (a,-b) \\
g((a,b)) & = (-a,b) \\
h((a,b)) & = (b,a) \\
k((a,b)) & = (-b,-a) \\
\end{aligned}すると、
\begin{aligned}
f((2,1)) & = (2,-1) \\
g((2,1)) & = (-2,1) \\
h((2,1)) & = (1,2) \\
k((2,1)) & = (-1,-2) \\
\end{aligned}です。ここから、点 P は各オペレーションの組み合わせにより (±2,±1) , (±1,±2) (複号任意)のいずれかに遷移しそうだ、と予測できます。
実際、
\begin{aligned}
f((-2,1)) & = (-2,-1) \\
g((1,2)) & = (-1,2) \\
h((-2,1)) & = (1,-2) \\
\end{aligned}です。小問1は証明不要なので、この8点を答えに書けばOKです(図1)。
ここでもし、この8点以外には遷移しないことの証明を求められたらどうするか、考えてみましょう。
n = 1 のときを初期状態とするとき、 n ≦ 2 において P はこれら8点のいずれかにいることが示せているので、一番プリミティブなやり方は各8点の遷移先が8点のいずれかであることをすべて書き下すことです。32通りも書かなければならないのはうんざりしますが、これが一番確実でしょう。
これを言葉で表現すると、写像 f,g,h,k の動作はいずれも二次元座標系の点 (a,b) の符号を反転させるか、座標を入れ替えるかのいずれかなので、それらは明らかに集合 { (±2,±1) , (±1,±2) (複号任意)} 上で閉じている、といった感じになります。ちょっとモヤっとしますが、まあ大丈夫でしょう。
2024年東大 数学 第3問 小問2の解法
点 P の遷移先を、最初にいたA(2,1) から座標平面上の原点を中心にして半時計回りに B(1,2) , C(-1,2) ,D(-2,1) , E(-2.-1) , F(-1,-2) , G(1,-2) , H(2,-1) と名付けます(図2)。
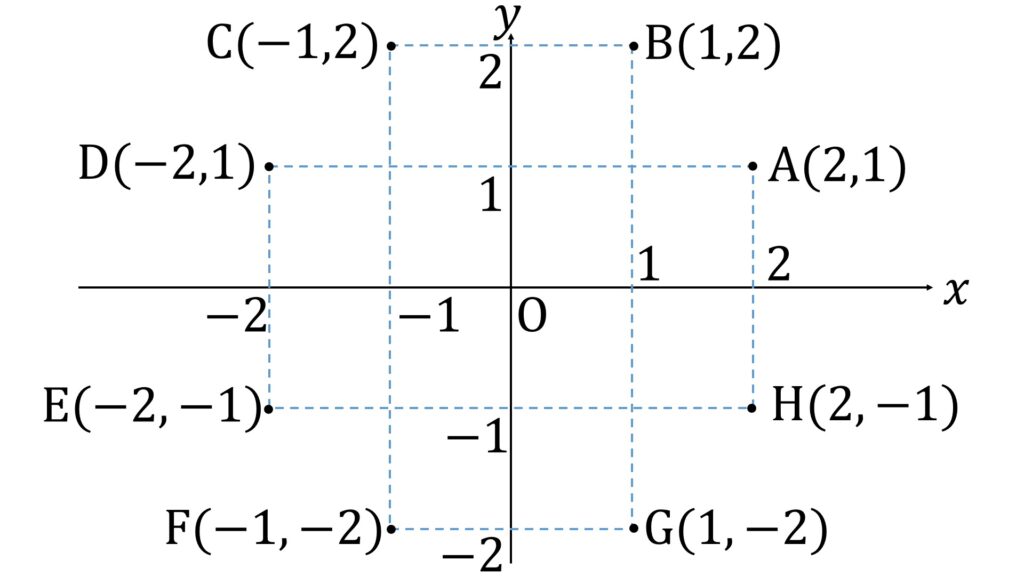
また、P が n 秒後に各点にいる確率を順に a_n,b_n,c_n,d_n,e_n,f_n,g_n,h_n と置きます。すると明らかに
\begin{aligned}
& a_n+b_n+c_n+d_n \\
+ & e_n+f_n+g_n+h_n \\
= &1
\end{aligned}が成り立ちます。初期状態を n = 0 であると定義すると、 P は最初 A にいるので、
\begin{aligned}
& a_0=1 \\
& b_0=c_0=d_0=e_0=f_0=g_0=h_0=0
\end{aligned}です。
このとき、証明すべき事柄は n ≧ 1のとき a_n= e_n が成り立つことです。
そこでまず、 a_n, e_n が満たす漸化式を求めます。
\begin{aligned}
f(\mathrm{A}) & = \mathrm{H} \\
g(\mathrm{A}) & = \mathrm{D} \\
h(\mathrm{A}) & = \mathrm{B} \\
k(\mathrm{A}) & = \mathrm{F} \\
\end{aligned}ですが、各写像とも2回施すともとに戻るので、
\begin{aligned}
f(\mathrm{H}) & =f(f(\mathrm{A}) ) = \mathrm{A} \\
g(\mathrm{D} ) & = g(g(\mathrm{A})) = \mathrm{A} \\
h(\mathrm{B}) & = h( h(\mathrm{A}) ) = \mathrm{A} \\
k(\mathrm{F} ) & =k(k(\mathrm{A}) ) = \mathrm{A} \\
\end{aligned}が成り立ちます。
A からの遷移先は B,D,F,H の4点なので、 A への遷移元もこの4点しかありません。
これ以外の点から A に遷移してくることはありません。もしそのような点 X があったとすると、ある写像 x が存在して、
x( \mathrm{X}) = \mathrm{A}なので
x( \mathrm{A}) = \mathrm{X}が成り立つはずです。 x はf,g,h,k のいずれかなので、これは X が B,D,F,H のいずれでもないことに矛盾します。
f,g が施される確率が \displaystyle\frac{1}3 、 h,k が施される確率が \displaystyle\frac{1}6 なので、 n ≧ 1 のとき
a_n = \frac{1}3 d_{n-1} + \frac{1}3 h_{n-1} + \frac{1}6 b_{n-1} + \frac{1}6 f_{n-1}が成り立ちます。
同様に
\begin{aligned}
f(\mathrm{E}) & = \mathrm{D} \\
g(\mathrm{E}) & = \mathrm{H} \\
h(\mathrm{E}) & = \mathrm{F} \\
k(\mathrm{E}) & = \mathrm{B} \\
\end{aligned}なので
\begin{aligned}
f(\mathrm{D}) & = \mathrm{E} \\
g(\mathrm{H} ) & = \mathrm{E} \\
h(\mathrm{F}) & = \mathrm{E} \\
k(\mathrm{B} ) & = \mathrm{E} \\
\end{aligned}が成り立ちます。
したがって an のときと同様、 n ≧ 1 のとき
e_n = \frac{1}3 d_{n-1} + \frac{1}3 h_{n-1} + \frac{1}6 b_{n-1} + \frac{1}6 f_{n-1}です。
ゆえに n ≧ 1のとき a_n= e_n が成り立ちます。
2024年東大 数学 第3問 小問3の解法
まず、小問2の手法で bn = fn , cn=gn , dn = hn が言えることに注意します。これは n ≧ 1 のときに成り立ちますが、 b_0=c_0=d_0=e_0=f_0=g_0=h_0=0 なので実は n = 0 のときも成り立ちます。
したがって n ≧ 1のとき、小問2で導出した漸化式より
\begin{aligned}
a_n & = \frac{1}3 d_{n-1} + \frac{1}3 h_{n-1} + \frac{1}6 b_{n-1} + \frac{1}6 f_{n-1} \\
& = \frac{2}3 d_{n-1} + \frac{1}3 b_{n-1} \\
\end{aligned}が成り立ちます。
漸化式に bn と dn が含まれるので、これらの漸化式を求めます。小問2と同じやり方で n ≧ 1のとき
\begin{aligned}
b_n & = \frac{1}3 c_{n-1} + \frac{1}3 g_{n-1} + \frac{1}6 a_{n-1} + \frac{1}6 e_{n-1} \\
d_n & = \frac{1}3 a_{n-1} + \frac{1}3 e_{n-1} + \frac{1}6 c_{n-1} + \frac{1}6 g_{n-1} \\
\end{aligned}であることが言えるので、 n ≧ 2 のとき
\begin{aligned}
b_n & = \frac{2}3 c_{n-1} + \frac{1}3 a_{n-1} \\
d_n & = \frac{2}3 a_{n-1} + \frac{1}3 c_{n-1} \\
\end{aligned}が成り立ちます。 a0 ≠ e0 なので、 n = 1 のときは成り立たないことに注意しましょう。
今度は漸化式に cn が現れたので、上記と同じように n ≧ 1のとき
\begin{aligned}
c_n & = \frac{1}3 b_{n-1} + \frac{1}3 f_{n-1} + \frac{1}6 d_{n-1} + \frac{1}6 h_{n-1} \\
& = \frac{2}3 b_{n-1} + \frac{1}3 d_{n-1} \\
\end{aligned}が成り立ちます。
単に代入するだけではいつまでたっても an だけの漸化式になりそうにないので、式の対称性に着目します。
\begin{aligned}
a_n & = \frac{1}3 b_{n-1} + \frac{2}3 d_{n-1} \\
c_n & = \frac{2}3 b_{n-1} + \frac{1}3 d_{n-1} \\
\end{aligned}なので、辺々足して
a_n +c_n = b_{n-1} +d_{n-1}です。また、辺々引いて
a_n -c_n = -\frac{1}3 (b_{n-1} -d_{n-1})が成り立ちます。
同様にして、
\begin{aligned}
b_n & = \frac{1}3 a_{n-1} + \frac{2}3 c_{n-1} \\
d_n & = \frac{2}3 a_{n-1} + \frac{1}3 c_{n-1} \\
\end{aligned}の辺々を足したり引いたりして
\left \{
\begin{aligned}
b_n +d_n &= a_{n-1} +c_{n-1} \\
b_n -d_n &= - \frac{1}3 (a_{n-1} -c_{n-1}) \\
\end{aligned}
\right .を得ます。
したがって n ≧ 3 のとき
\left \{
\begin{aligned}
a_n +c_n &= a_{n-2} +c_{n-2} \\
a_n -c_n &= \frac{1}9 (a_{n-2} -c_{n-2}) \\
\end{aligned}
\right .が成り立ちます。
これらを an + cn および an – cn の漸化式と見立てることで、 n が2以上の偶数のとき
\left \{
\begin{aligned}
a_n +c_n &= a_{2} +c_{2} \\
a_n -c_n &= \left ( \frac{1}9 \right )^{\frac{n-2}2 } (a_{2} -c_{2}) \\
\end{aligned}
\right .n が奇数のとき
\left \{
\begin{aligned}
a_n +c_n &= a_{1} +c_{1} \\
a_n -c_n &= \left ( \frac{1}9 \right )^{\frac{n-1}2 } (a_{1} -c_{1}) \\
\end{aligned}
\right .が成り立ちます。
a_1 =c_1 = 0 、 a_2 = \displaystyle\frac{5}{18} 、 c_2 = \displaystyle\frac{2}9 なので、 n が2以上の偶数のとき
\left \{
\begin{aligned}
a_n +c_n &= \frac{1}2 \\
a_n -c_n &= \left ( \frac{1}9 \right )^{\frac{n-2}2 } \cdot \frac{1}{18} = \frac{1}2 \cdot \left ( \frac{1}3 \right )^n\\
\end{aligned}
\right .n が奇数のとき
\left \{
\begin{aligned}
a_n +c_n &= 0 \\
a_n -c_n &= 0 \\
\end{aligned}
\right .です。
ゆえに n が正の整数のとき、 n 秒後に P が A(2,1) にいる確率は n が偶数のとき
\frac{1}4\left ( 1 + \frac{1}{3^n} \right)n が奇数のとき
0
です。
解法のポイント

本問は連立確率漸化式問題のバリエーションです。複数の確率変数をとりあえず複数の漸化式で表現して、あとで単一の確率変数の漸化式にまとめる、と言うアプローチはオーソドックスなものなので、是非マスターしておいてください。
